探索勾股定理[下学期]
图片预览

文档简介
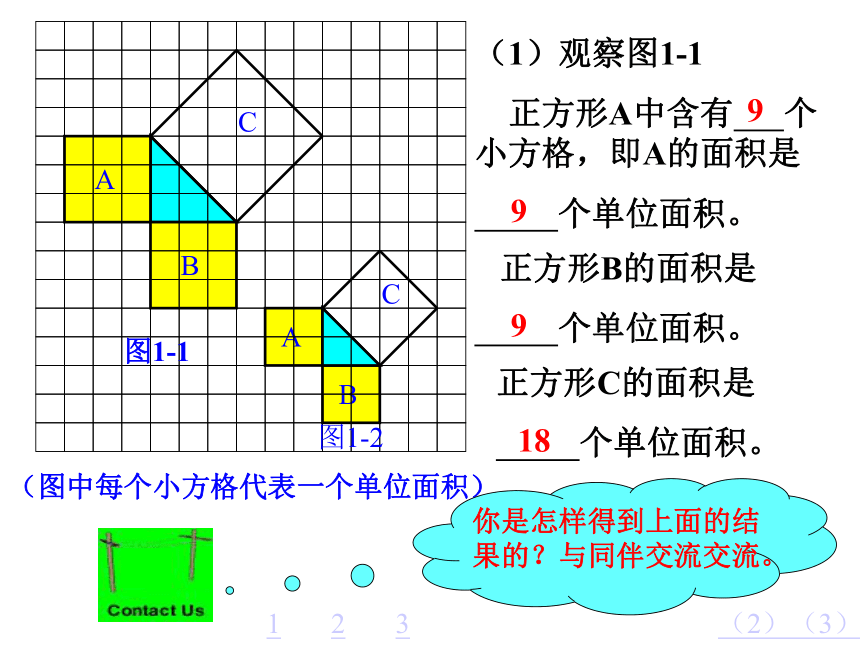
课件22张PPT。探索勾股定理执教:曲阜实验中学 刘老师制作:行云流水(1)观察图1-1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
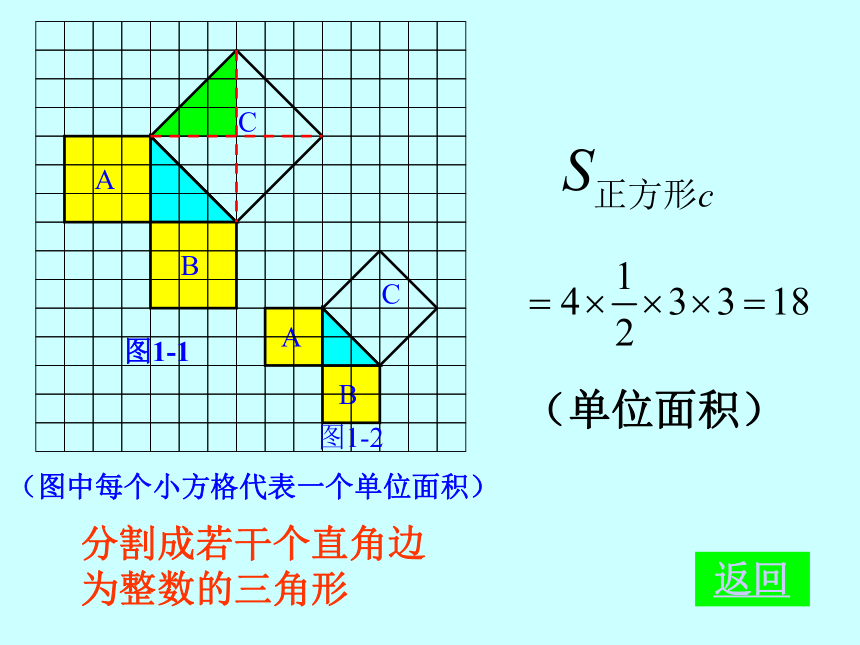
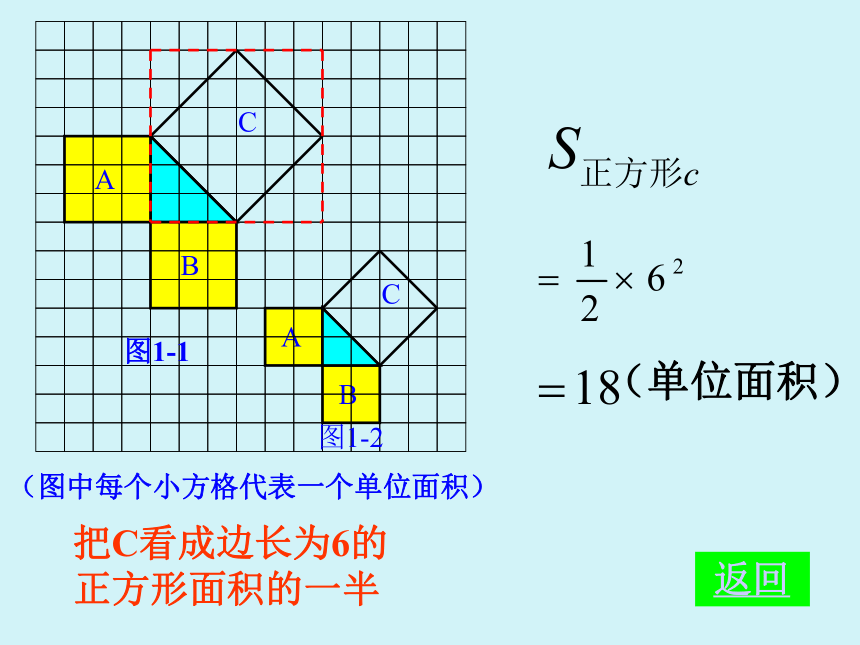
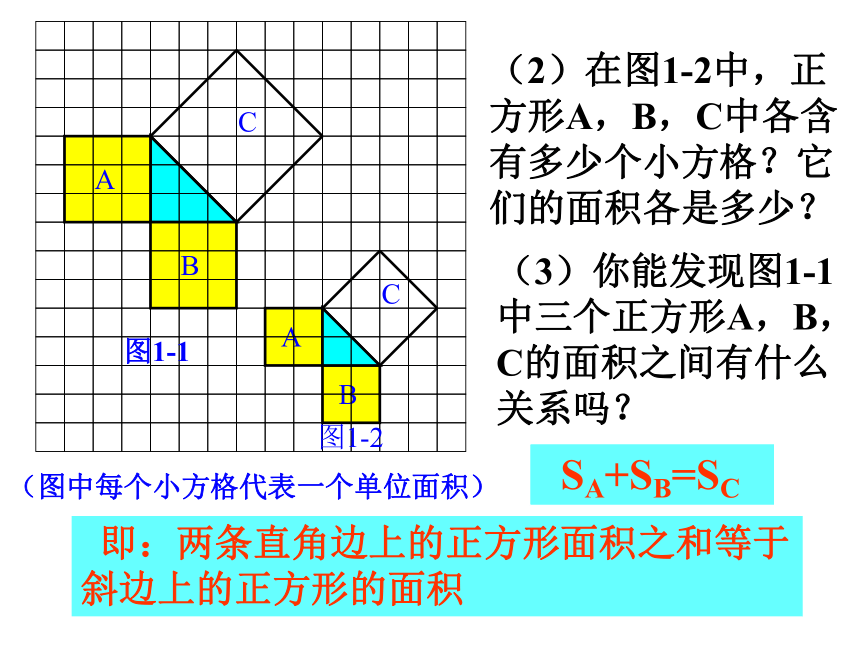
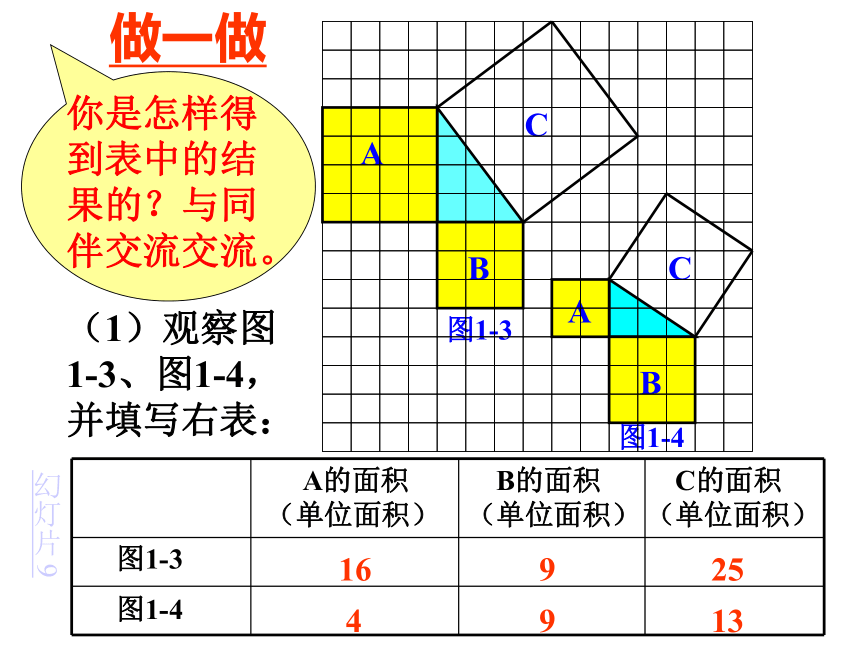
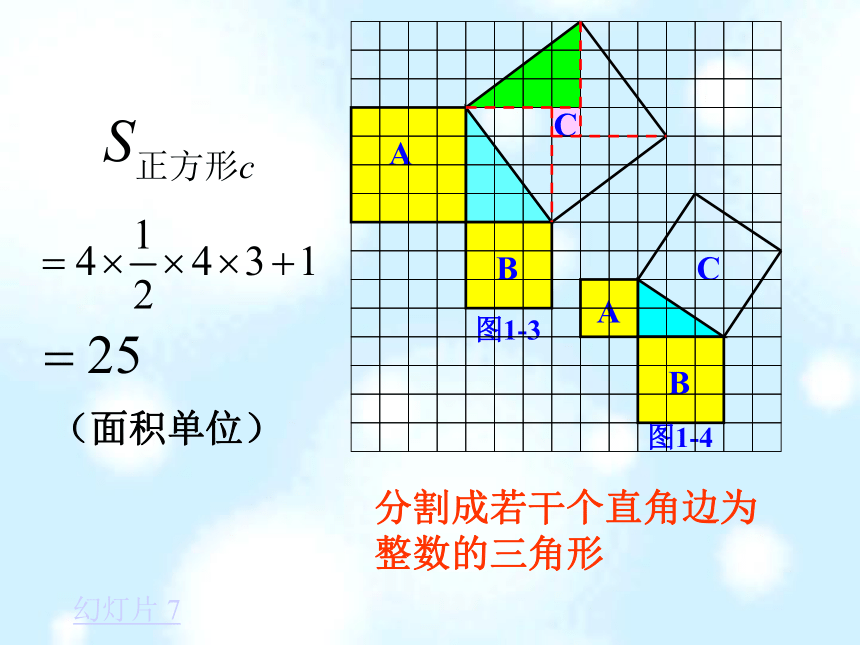
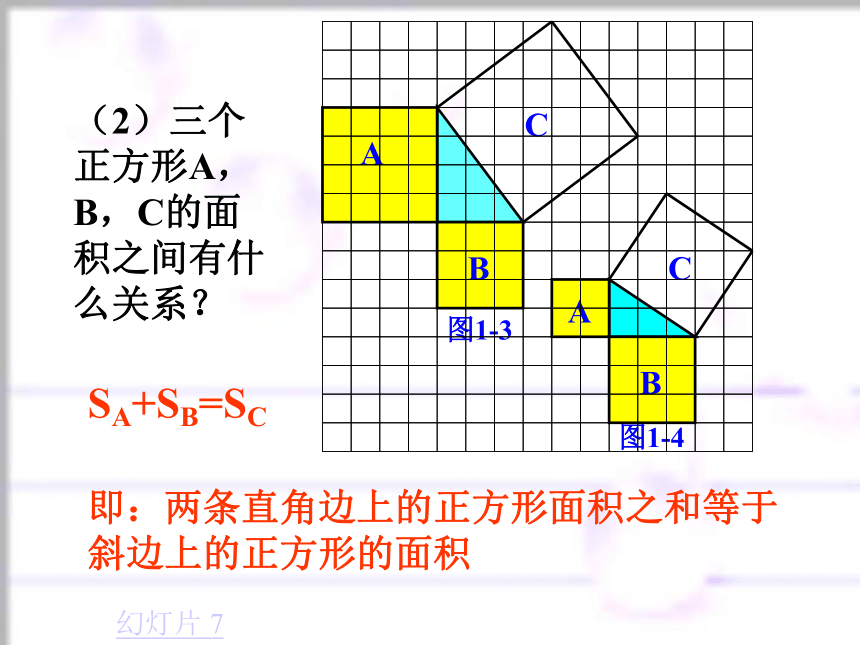
个单位面积。99918123(2)(3)分割成若干个直角边为整数的三角形(单位面积) 返回(单位面积)把C看成边长为6的正方形面积的一半 返回(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积(1)观察图1-3、图1-4,并填写右表: A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图1-3图1-4169254913做一做幻灯片 9分割成若干个直角边为整数的三角形(面积单位)幻灯片 7(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
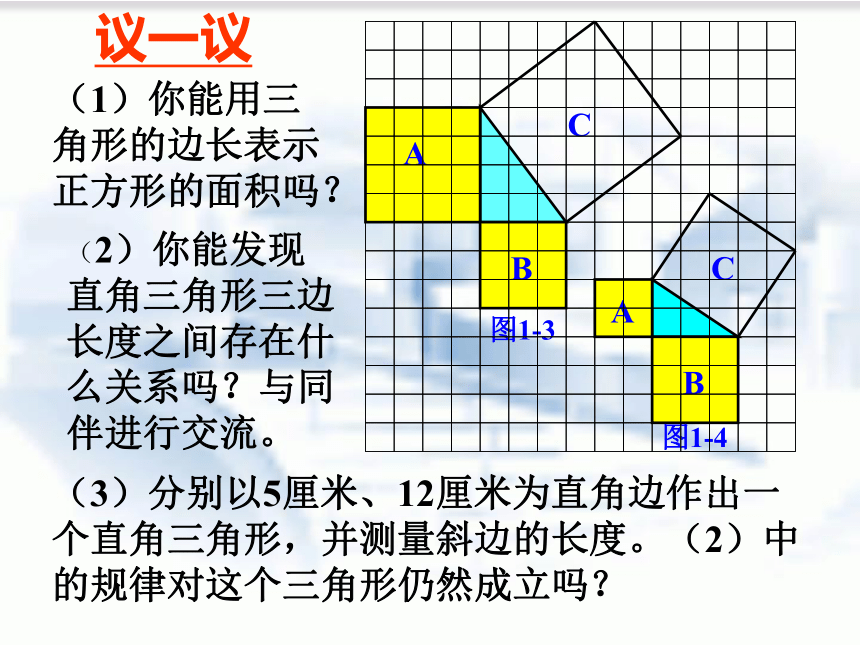
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积幻灯片 7(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?议一议 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦勾股定理也可以用数学语言表示为:
acbACB 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米请同学们画四个与右图全等的直角三角形,并把它剪下来。用这四个三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。
作业一、P6 习题1.1 第1、2、3、4题二、准备4张全等的直角三角形纸片abc你还有其它验证勾股定理的方法吗?aaaabbbbcccc 有人利用这4个直角三角 形拼出了右图,你能用两种方法表示大正方形的面积吗? 大正方形的面积可以表示为 —————————— 又可以表示为:——————— 对比两种表示方法,你得到勾股定理了吗?(a+b)2c+1/2ab?4 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.?6841?244.8小结说说这节课你有什么收获?再见
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918123(2)(3)分割成若干个直角边为整数的三角形(单位面积) 返回(单位面积)把C看成边长为6的正方形面积的一半 返回(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1-1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积(1)观察图1-3、图1-4,并填写右表: A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图1-3图1-4169254913做一做幻灯片 9分割成若干个直角边为整数的三角形(面积单位)幻灯片 7(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积幻灯片 7(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度。(2)中的规律对这个三角形仍然成立吗?议一议 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦勾股定理也可以用数学语言表示为:
acbACB 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米请同学们画四个与右图全等的直角三角形,并把它剪下来。用这四个三角形拼一拼、摆一摆,看看是否得到一个含有以斜边c为边长的正方形,你能利用它说明勾股定理吗?并与同伴交流。
作业一、P6 习题1.1 第1、2、3、4题二、准备4张全等的直角三角形纸片abc你还有其它验证勾股定理的方法吗?aaaabbbbcccc 有人利用这4个直角三角 形拼出了右图,你能用两种方法表示大正方形的面积吗? 大正方形的面积可以表示为 —————————— 又可以表示为:——————— 对比两种表示方法,你得到勾股定理了吗?(a+b)2c+1/2ab?4 课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( ) 二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.?6841?244.8小结说说这节课你有什么收获?再见
