勾股定理的逆定理[下学期]
文档属性
| 名称 | 勾股定理的逆定理[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-22 21:51:00 | ||
图片预览




文档简介
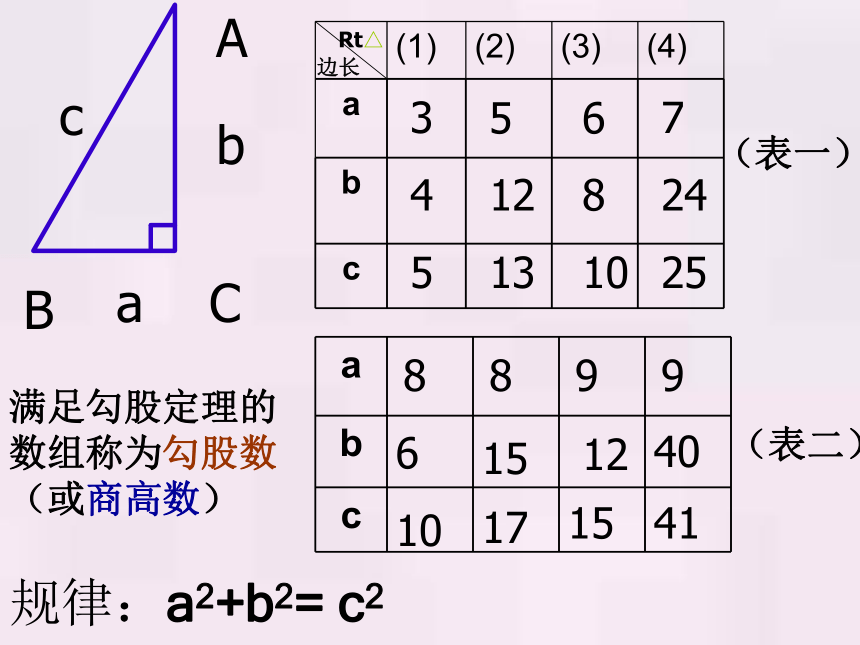
课件16张PPT。经过证明被确认正确的命题叫做定理
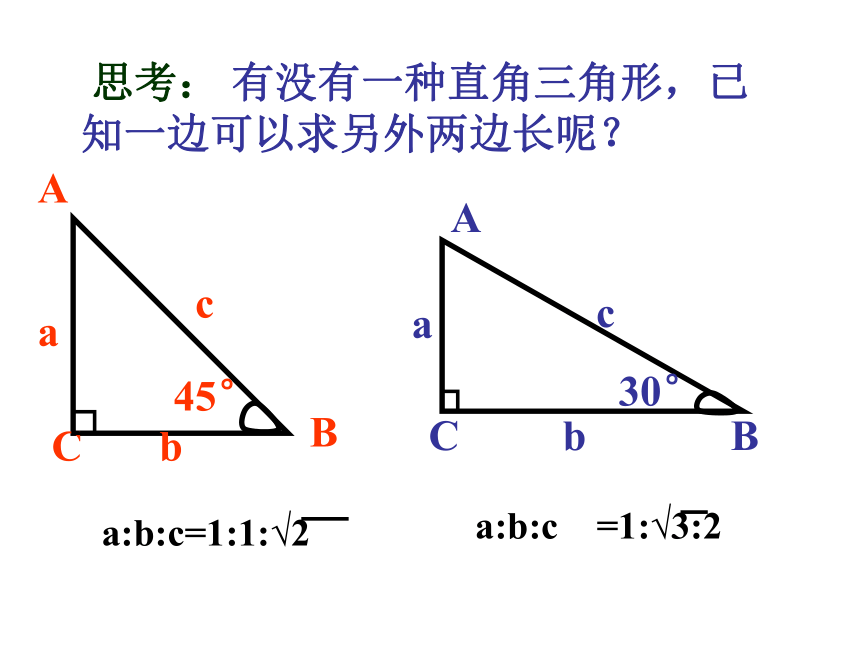
abcACB规律:a2+b2= c2
3
4
55
12
136
8
107
24
258899Rt△边长6
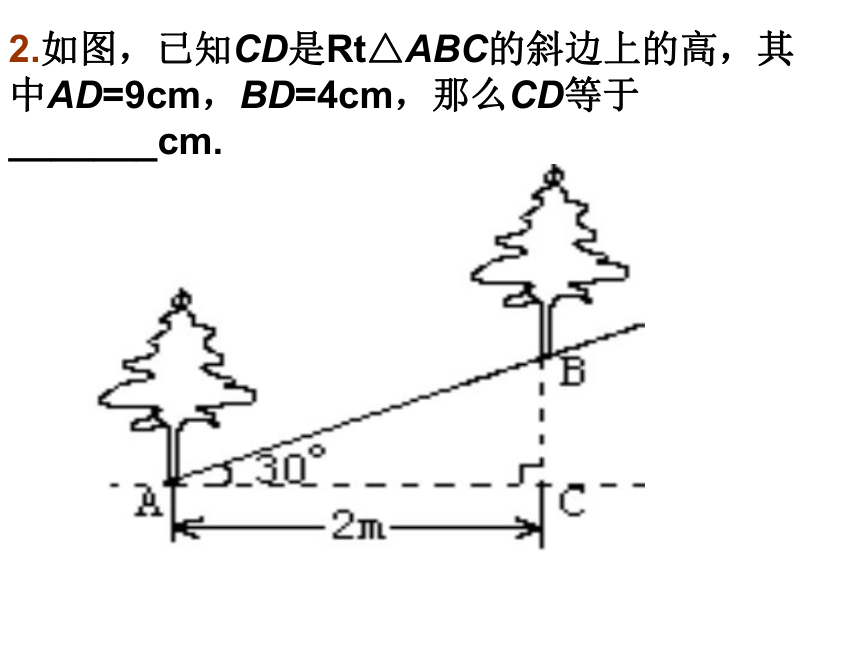
10124017154115(表一)(表二)满足勾股定理的数组称为勾股数(或商高数) 思考: 有没有一种直角三角形,已知一边可以求另外两边长呢? a:b:c =1:√3:2勾股定理的逆定理 如果三角形的三边长a,b,c有关系 那么这个三角形是直角三角形.1.有两棵树,一棵高6米,另一棵高2米,两树相距5米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米.2.如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于_______cm. 3.在一直角三角形中三边为a=3,b=4,则c=5或4.一直角三角形的木版,三边的平方为1800cm2,则斜边长为___ cm 5.如图5,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A.10米 B.15米
C.25米 D.30米图56.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针A向在l上转动两次,使它转到△A’’B’’C’’的位置.设BC=1,AC=则顶点A运动到点A’’的位置时,点A经过的路线长是 (计算结果不取近似值). 78. 如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点C与点B重合,求折痕DE的长。 x4-x345方程思想9. 如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45o的B处,往东航行20海里后达到该岛南偏西30o的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?计算后说明理由。 如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由.
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt⊿ABC中,∠BAC = 90o ,所以有: ( x + 0.5 )2 = x2 + 22
abcACB规律:a2+b2= c2
3
4
55
12
136
8
107
24
258899Rt△边长6
10124017154115(表一)(表二)满足勾股定理的数组称为勾股数(或商高数) 思考: 有没有一种直角三角形,已知一边可以求另外两边长呢? a:b:c =1:√3:2勾股定理的逆定理 如果三角形的三边长a,b,c有关系 那么这个三角形是直角三角形.1.有两棵树,一棵高6米,另一棵高2米,两树相距5米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米.2.如图,已知CD是Rt△ABC的斜边上的高,其中AD=9cm,BD=4cm,那么CD等于_______cm. 3.在一直角三角形中三边为a=3,b=4,则c=5或4.一直角三角形的木版,三边的平方为1800cm2,则斜边长为___ cm 5.如图5,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为( )
A.10米 B.15米
C.25米 D.30米图56.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针A向在l上转动两次,使它转到△A’’B’’C’’的位置.设BC=1,AC=则顶点A运动到点A’’的位置时,点A经过的路线长是 (计算结果不取近似值). 78. 如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点C与点B重合,求折痕DE的长。 x4-x345方程思想9. 如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45o的B处,往东航行20海里后达到该岛南偏西30o的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?计算后说明理由。 如图,有一块塑料矩形模板ABCD,长为10cm,宽为4cm,将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合),在AD上适当移动三角板顶点P:
①能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时 AP 的长;若不能,请说明理由.
②再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH 始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2cm?若能,请你求出这时AP的长;若不能,请你说明理由.想一想:印度有一数学家婆什迦罗曾提出过“荷花问题”:“平平湖水清可鉴, 面上半尺生红莲;
出泥不染亭亭立, 忽被强风吹一边。
渔人观看忙向前, 花离原位二尺远;
能算诸君请解题, 湖水如何知深浅?”分析:先把实际问题转化成数学问题。求:AB的长根据勾股定理得: 解得 x = 3.75 (尺)答:湖水深3.75尺。解:设AB= x,则BD = x + 0.5,所以BC = BD = x + 0.5,在Rt⊿ABC中,∠BAC = 90o ,所以有: ( x + 0.5 )2 = x2 + 22
