13.4课题学习 最短路径问题解答题巩固练习(含解析)
文档属性
| 名称 | 13.4课题学习 最短路径问题解答题巩固练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 10:00:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级数学上册最短路径问题解答题巩固练习
1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
2.在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
3.如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
4.(1)若P为x轴上一动点,A(2,2),B(4,4),求PA+PB最小值?
(2)若P为半径为1的⊙O上一动点,O(0,0),A(2,2),B(4,4),求PA+PB的最小值?
5.如图,M,N分别为AC,BC边上的两定点,在AB上求一点P,使△PMN的周长最小,并说明理由.
6.如图,角形铁架∠MON小于60°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
7.如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
8.已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
(1)找到A、B点,保留作图痕迹;
(2)求此时∠APB等于多少度?如果∠MON=θ,∠APB又等于多少?
9.如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
10.如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
11.如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
12.已知点A(2,3),B(5,9),在x轴上找一点C,使AC+BC最小并求出最小值.
13.如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
参考答案
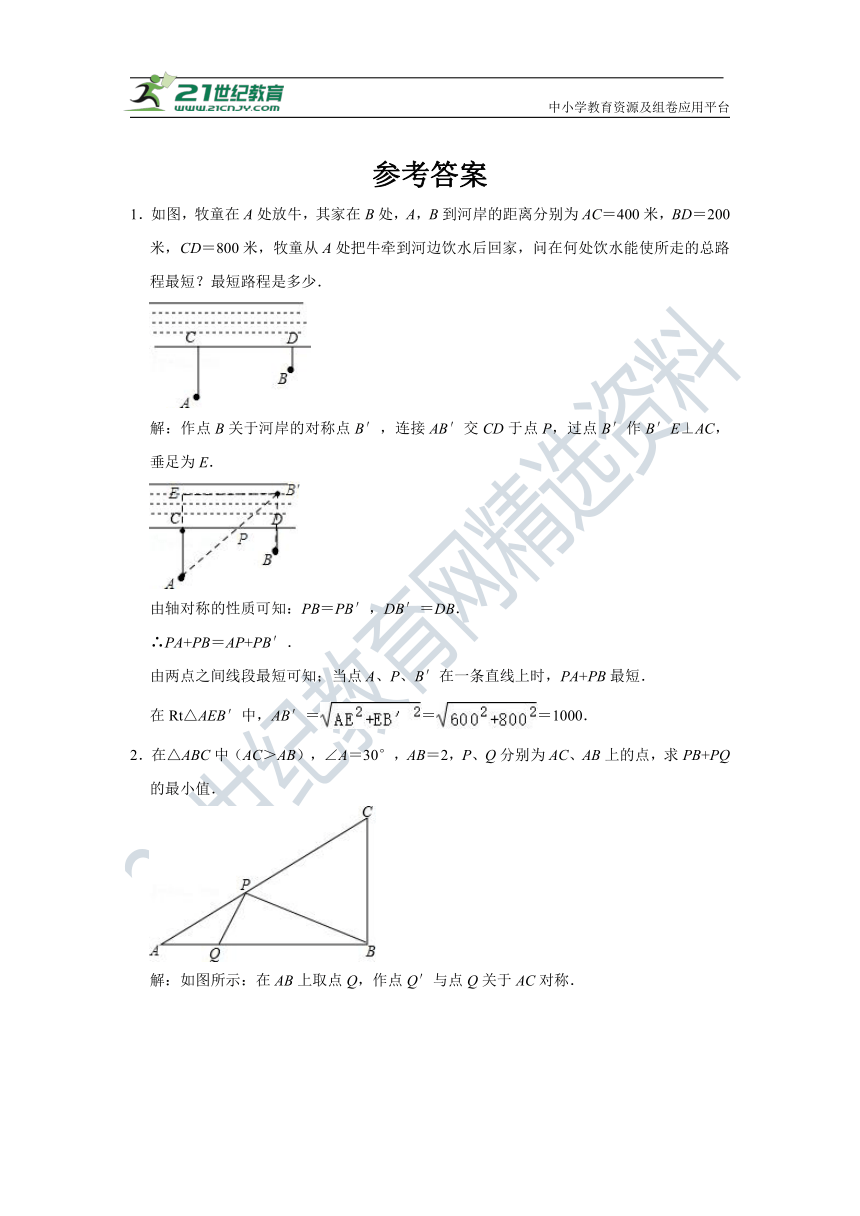
1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
解:作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E⊥AC,垂足为E.
由轴对称的性质可知:PB=PB′,DB′=DB.
∴PA+PB=AP+PB′.
由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.
在Rt△AEB′中,AB′===1000.
2.在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
解:如图所示:在AB上取点Q,作点Q′与点Q关于AC对称.
∵点Q′与点Q关于AC对称,
∴∠Q′AC=∠CAB=30°,QP=Q′P.
∴∠Q′AB=60°,PB+PQ=PB+PQ′=Q′B.
由垂线段最短可知:当Q′B⊥AQ′时,Q′B有最小值,Q′B的最小值=sin60° AB==.
∴PB+PQ的最小值为.
3.如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
解:作A关于x=3的对称点A′,连接A′B交直线x=3与点C.
∵点A与点A′关于x=3对称,
∴AC=A′C.
∴AC+BC=A′C+BC.
当点B、C、A′在同一条直线上时,A′C+BC有最小值,即△ABC的周长有最小值.
∵点A与点A′关于x=3对称,
∴点A′的坐标为(6,3).
设直线BA′的解析式y=kx+b,将点B和点A′的坐标代入得:,
解得:.
∴y=.
将x=3代入函数的解析式得y=.
∴y的值为.
4.(1)若P为x轴上一动点,A(2,2),B(4,4),求PA+PB最小值?
(2)若P为半径为1的⊙O上一动点,O(0,0),A(2,2),B(4,4),求PA+PB的最小值?
解:(1)如图1所示;作点A关于x轴的对称点A′.
由轴对称的性质可知点A′的坐标为(2,﹣2),
∵PA+PB=PA′+PB.
当点A′、P、B在一条直线上时,PA+PB有最小值.
由两点间的距离公式得:A′B==2.
∴PA+PB的最小值为2.
(2)如图2所示:当点A、B、P在一条直线上时,PA+PB有最小值.
由两点之间的距离公式得:OA==2,OB==4.
AP+PB=OA+OB﹣2OP=6﹣2.
∴PA+PB的最小值为6.
5.如图,M,N分别为AC,BC边上的两定点,在AB上求一点P,使△PMN的周长最小,并说明理由.
解:如图所示:
作点N关于直线AB的对称点N′,连接MN′交直线AB于点P,则PN=P′N,
由于△PMN的周长=PM+PN+MN,而MN是定值,
故点当M、N′、P在一条直线上时,三角形的周长有最小值.最小值等于MN+N′M.
6.如图,角形铁架∠MON小于60°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.
此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.
7.如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
解:作点B关于直线CD的对称点H,连接AH交CD于M,连接BM,则MA+MB最小,铺设水管的费用最节省,
作AE⊥BH于E,
∵CD=15,
∴AE=15,
EH=HD+ED=21,
∴AH==26,
26×3=78万.
答:总费用是78万.
8.已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
(1)找到A、B点,保留作图痕迹;
(2)求此时∠APB等于多少度?如果∠MON=θ,∠APB又等于多少?
解:(1)如图所示:
(2)如图下图所示:连AP、BP.
∵点A′与点P关于直线OM对称,点B′与点P关于ON对称,
∴A′P⊥OM,B′P⊥ON,A′A=AP,B′B=BP.
∴∠A′=∠APA′,∠B′=∠BPB′.
∵A′P⊥OM,B′P⊥ON,
∴∠MON+∠A′PB′=180°.
∴∠A′PB′=180°﹣40°=140°.
在△A′B′P中,由三角形的内角和定理可知:∠A′+∠B′=180°﹣140°=40°.
∴∠A′PA+∠BPB′=40°.
∴∠APB=140°﹣40=100°.
如果∠MON=θ,则∠A′PB′=180°﹣θ.
在△A′B′P中,由三角形的内角和定理可知:∠A′+∠B′=θ.
∴∠A′PA+∠BPB′=θ.
∴∠APB=180°﹣2θ.
9.如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.
此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.
连接DD′,AA′,OA′,OD′.
∵OA=OA′,∠AOA′=60°,
∴∠OAA′=∠OA′A=60°,
∴△ODD′是等边三角形.
同理△OAA′也是等边三角形.
∴OD'=OD=6,OA′=OA=10,
∠D′OA′=90°.
∴A′D′==2.
10.如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
解:如图所示:
过点C作CO⊥AB于O,延长CO到C′,使OC′=OC;
连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小;
连接BC′,由轴对称的性质得:∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=2,
∵D是BC边的中点,
∴BD=1,
根据勾股定理得:DC′===;
∴DE+CE的最小值为.
11.如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
解:作Q关于AC的对称点D,连接PQ,CD,
则AC垂直平分QD,
∴PQ=PD,CQ=CD=BC=1,∠DCP=∠QCP,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴BD2=BC2+CD2=5,
∴BD=,
∴△PBQ周长的最小值=BQ+BP+PQ=BQ+BD=1+.
答:△PBQ周长的最小值为1+.
12.已知点A(2,3),B(5,9),在x轴上找一点C,使AC+BC最小并求出最小值.
解:点A关于x轴的对称点A′的坐标为(2,﹣3).
设直线A′B的解析式y=kx+b(k≠0),
将点A′(2,﹣3)和B(5,9)的坐标代入得:
解得:
所以直线A′B的解析式为:y=4x﹣11.
令y=0,解得x=
所以点C的坐标为(,0).
此时:AC+BC=A′B==3.
故AC+BC的最小值为3.
13.如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
解:如图所示:连接ED交AC与点P.
∵四边形ABCD是正方形,
∴点B与点D关于AC对称.
∴PB=PD.
∴PE+PB=PD+EP.
由两点之间线段最短可知:当点E、P、D在一条直线上时,PE+PB有最小值,最小值为ED.
在Rt△ADE中,ED==5.
八年级数学上册最短路径问题解答题巩固练习
1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
2.在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
3.如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
4.(1)若P为x轴上一动点,A(2,2),B(4,4),求PA+PB最小值?
(2)若P为半径为1的⊙O上一动点,O(0,0),A(2,2),B(4,4),求PA+PB的最小值?
5.如图,M,N分别为AC,BC边上的两定点,在AB上求一点P,使△PMN的周长最小,并说明理由.
6.如图,角形铁架∠MON小于60°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
7.如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
8.已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
(1)找到A、B点,保留作图痕迹;
(2)求此时∠APB等于多少度?如果∠MON=θ,∠APB又等于多少?
9.如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
10.如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
11.如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
12.已知点A(2,3),B(5,9),在x轴上找一点C,使AC+BC最小并求出最小值.
13.如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
参考答案
1.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.
解:作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E⊥AC,垂足为E.
由轴对称的性质可知:PB=PB′,DB′=DB.
∴PA+PB=AP+PB′.
由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.
在Rt△AEB′中,AB′===1000.
2.在△ABC中(AC>AB),∠A=30°,AB=2,P、Q分别为AC、AB上的点,求PB+PQ的最小值.
解:如图所示:在AB上取点Q,作点Q′与点Q关于AC对称.
∵点Q′与点Q关于AC对称,
∴∠Q′AC=∠CAB=30°,QP=Q′P.
∴∠Q′AB=60°,PB+PQ=PB+PQ′=Q′B.
由垂线段最短可知:当Q′B⊥AQ′时,Q′B有最小值,Q′B的最小值=sin60° AB==.
∴PB+PQ的最小值为.
3.如图,点C的坐标为(3,y),使△ABC的周长最短,求y的值.
解:作A关于x=3的对称点A′,连接A′B交直线x=3与点C.
∵点A与点A′关于x=3对称,
∴AC=A′C.
∴AC+BC=A′C+BC.
当点B、C、A′在同一条直线上时,A′C+BC有最小值,即△ABC的周长有最小值.
∵点A与点A′关于x=3对称,
∴点A′的坐标为(6,3).
设直线BA′的解析式y=kx+b,将点B和点A′的坐标代入得:,
解得:.
∴y=.
将x=3代入函数的解析式得y=.
∴y的值为.
4.(1)若P为x轴上一动点,A(2,2),B(4,4),求PA+PB最小值?
(2)若P为半径为1的⊙O上一动点,O(0,0),A(2,2),B(4,4),求PA+PB的最小值?
解:(1)如图1所示;作点A关于x轴的对称点A′.
由轴对称的性质可知点A′的坐标为(2,﹣2),
∵PA+PB=PA′+PB.
当点A′、P、B在一条直线上时,PA+PB有最小值.
由两点间的距离公式得:A′B==2.
∴PA+PB的最小值为2.
(2)如图2所示:当点A、B、P在一条直线上时,PA+PB有最小值.
由两点之间的距离公式得:OA==2,OB==4.
AP+PB=OA+OB﹣2OP=6﹣2.
∴PA+PB的最小值为6.
5.如图,M,N分别为AC,BC边上的两定点,在AB上求一点P,使△PMN的周长最小,并说明理由.
解:如图所示:
作点N关于直线AB的对称点N′,连接MN′交直线AB于点P,则PN=P′N,
由于△PMN的周长=PM+PN+MN,而MN是定值,
故点当M、N′、P在一条直线上时,三角形的周长有最小值.最小值等于MN+N′M.
6.如图,角形铁架∠MON小于60°,A,D分别是OM,ON上的点,为实际设计的需要,需在OM和ON上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.
此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.
7.如图,A,B两个小集镇在河流CD的同侧,分别到河的距离为AC=6km,BD=15km,且CD=15km,现在要在河边建一自来水厂,向A,B两镇供水,铺设水管的费用为每千米3万.试在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少.
解:作点B关于直线CD的对称点H,连接AH交CD于M,连接BM,则MA+MB最小,铺设水管的费用最节省,
作AE⊥BH于E,
∵CD=15,
∴AE=15,
EH=HD+ED=21,
∴AH==26,
26×3=78万.
答:总费用是78万.
8.已知∠MON=40°,P为∠MON内一点,A为OM上的点,B为ON上的点,问当△PAB的周长取最小值时.
(1)找到A、B点,保留作图痕迹;
(2)求此时∠APB等于多少度?如果∠MON=θ,∠APB又等于多少?
解:(1)如图所示:
(2)如图下图所示:连AP、BP.
∵点A′与点P关于直线OM对称,点B′与点P关于ON对称,
∴A′P⊥OM,B′P⊥ON,A′A=AP,B′B=BP.
∴∠A′=∠APA′,∠B′=∠BPB′.
∵A′P⊥OM,B′P⊥ON,
∴∠MON+∠A′PB′=180°.
∴∠A′PB′=180°﹣40°=140°.
在△A′B′P中,由三角形的内角和定理可知:∠A′+∠B′=180°﹣140°=40°.
∴∠A′PA+∠BPB′=40°.
∴∠APB=140°﹣40=100°.
如果∠MON=θ,则∠A′PB′=180°﹣θ.
在△A′B′P中,由三角形的内角和定理可知:∠A′+∠B′=θ.
∴∠A′PA+∠BPB′=θ.
∴∠APB=180°﹣2θ.
9.如图,∠MON的边OM、ON上分别有点A、D,且∠MON=30°,OA=10,OD=6,B、C分别是边OM、ON上的动点,求AC+BC+BD的最小值.
解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.
此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.
连接DD′,AA′,OA′,OD′.
∵OA=OA′,∠AOA′=60°,
∴∠OAA′=∠OA′A=60°,
∴△ODD′是等边三角形.
同理△OAA′也是等边三角形.
∴OD'=OD=6,OA′=OA=10,
∠D′OA′=90°.
∴A′D′==2.
10.如图所示,在△ABC中,∠ACB=90°,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.
解:如图所示:
过点C作CO⊥AB于O,延长CO到C′,使OC′=OC;
连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小;
连接BC′,由轴对称的性质得:∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=2,
∵D是BC边的中点,
∴BD=1,
根据勾股定理得:DC′===;
∴DE+CE的最小值为.
11.如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
解:作Q关于AC的对称点D,连接PQ,CD,
则AC垂直平分QD,
∴PQ=PD,CQ=CD=BC=1,∠DCP=∠QCP,
∵△ABC为等腰直角三角形,AB=BC,
∴∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴BD2=BC2+CD2=5,
∴BD=,
∴△PBQ周长的最小值=BQ+BP+PQ=BQ+BD=1+.
答:△PBQ周长的最小值为1+.
12.已知点A(2,3),B(5,9),在x轴上找一点C,使AC+BC最小并求出最小值.
解:点A关于x轴的对称点A′的坐标为(2,﹣3).
设直线A′B的解析式y=kx+b(k≠0),
将点A′(2,﹣3)和B(5,9)的坐标代入得:
解得:
所以直线A′B的解析式为:y=4x﹣11.
令y=0,解得x=
所以点C的坐标为(,0).
此时:AC+BC=A′B==3.
故AC+BC的最小值为3.
13.如图1,点E是正方形ABCD边上一点,AE=3,BE=1,P为AC上的动点,在图2中作出点P,使得PB+PE最小(不写画法,保留作图痕迹),并计算PB+PE的最小值.
解:如图所示:连接ED交AC与点P.
∵四边形ABCD是正方形,
∴点B与点D关于AC对称.
∴PB=PD.
∴PE+PB=PD+EP.
由两点之间线段最短可知:当点E、P、D在一条直线上时,PE+PB有最小值,最小值为ED.
在Rt△ADE中,ED==5.
