勾股定理复习三课时[下学期]
文档属性
| 名称 | 勾股定理复习三课时[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-03 00:00:00 | ||
图片预览





文档简介
课件45张PPT。勾股定理
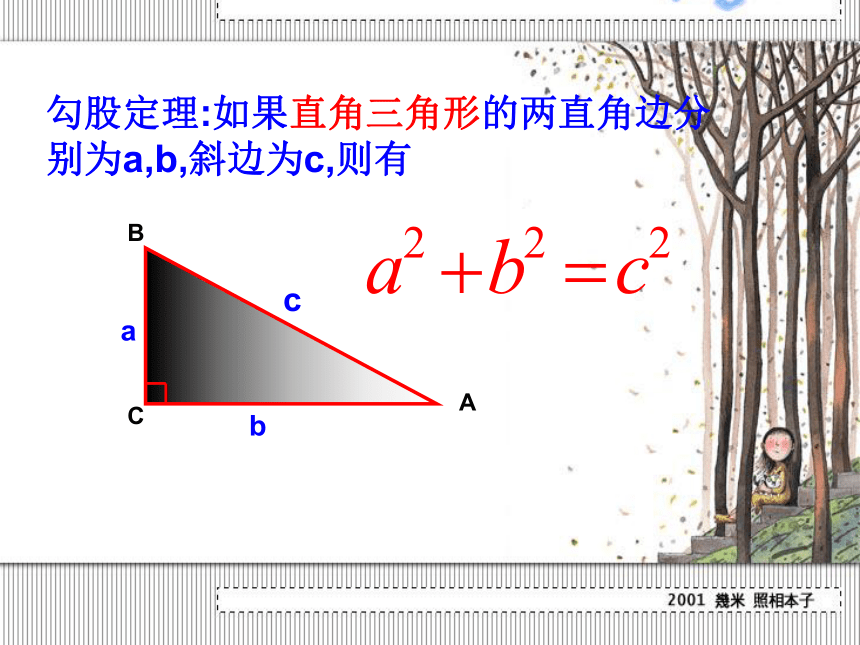
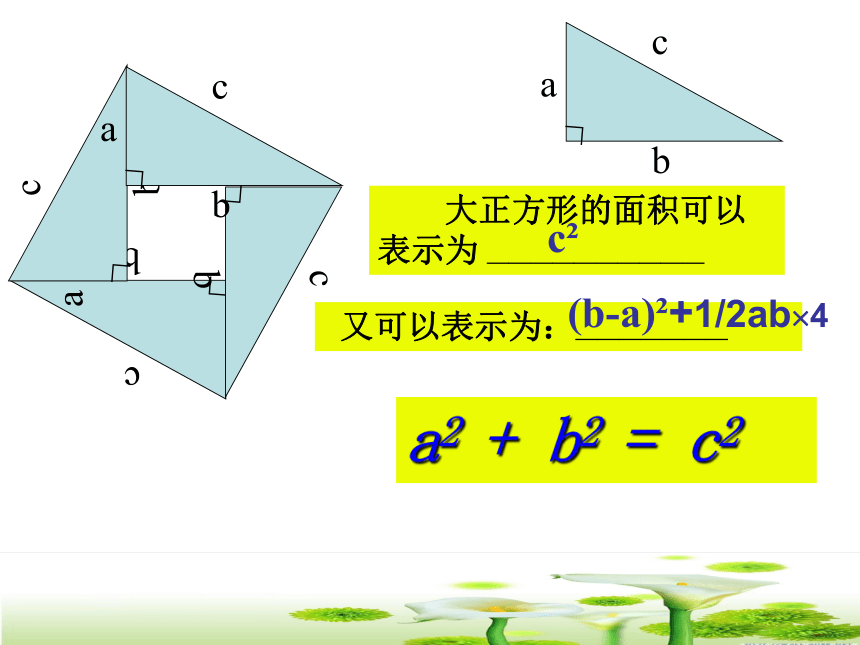
复习课第一课时勾股定理:如果直角三角形的两直角边分 别为a,b,斜边为c,则有 大正方形的面积可以表示为 —————————— 又可以表示为:———————c2(b-a)2+1/2ab?4
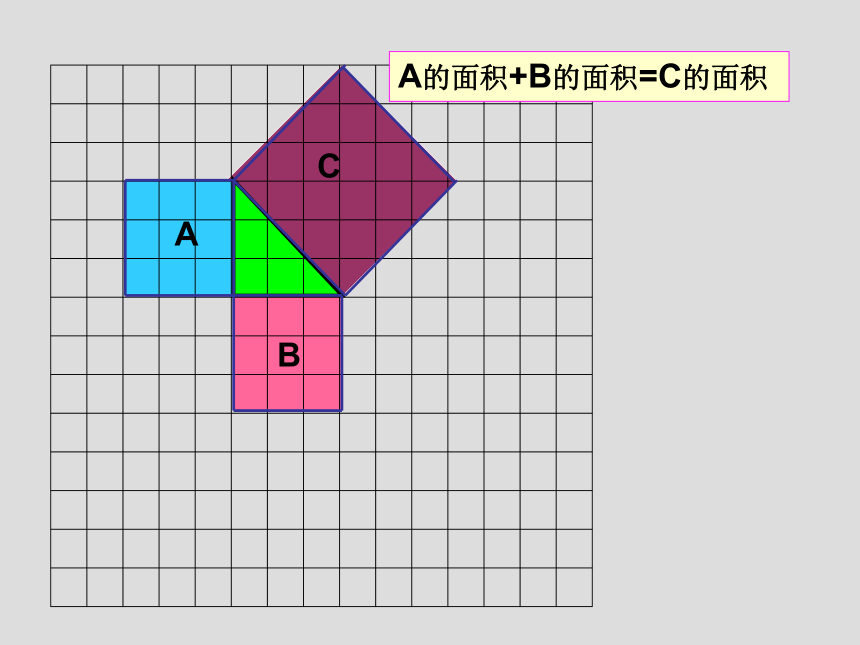
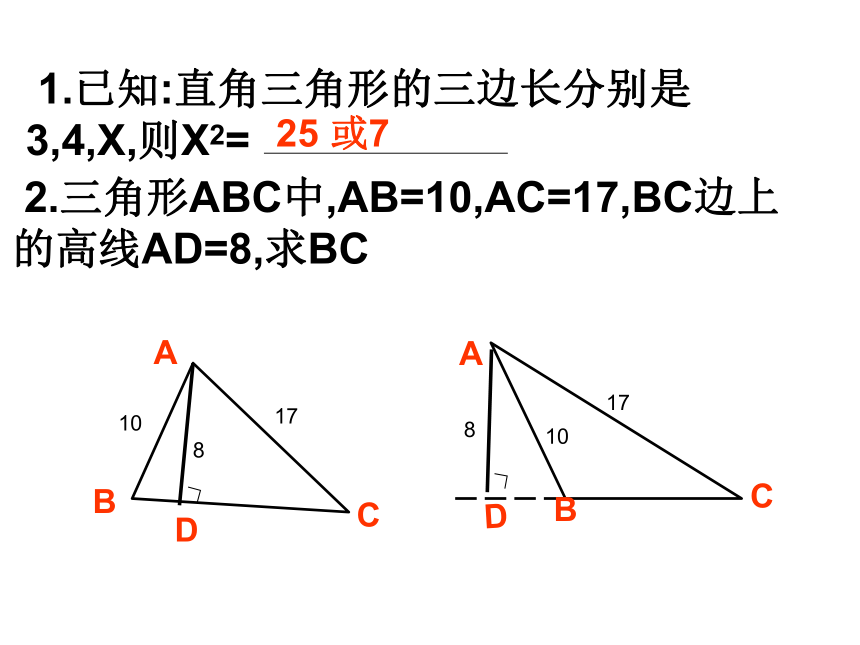
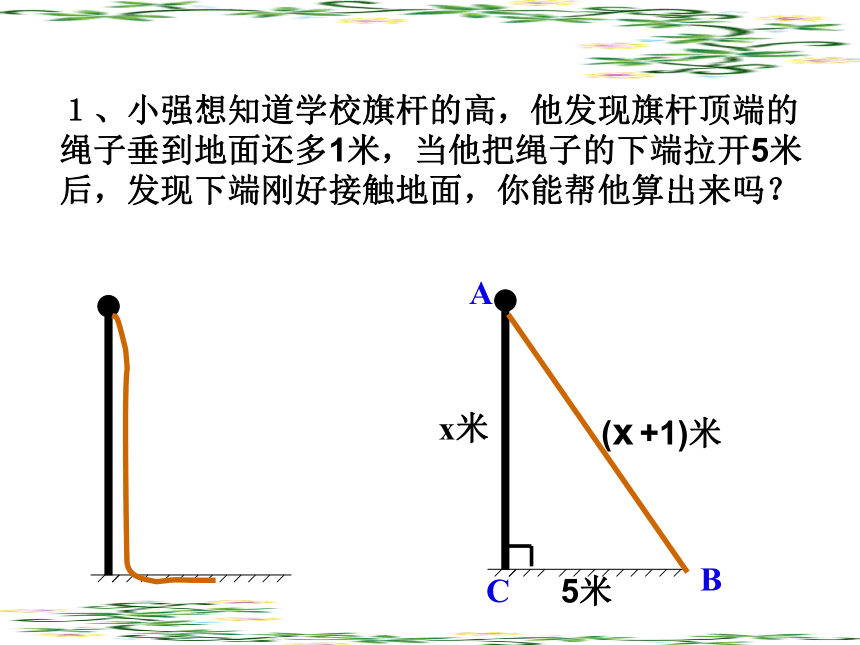
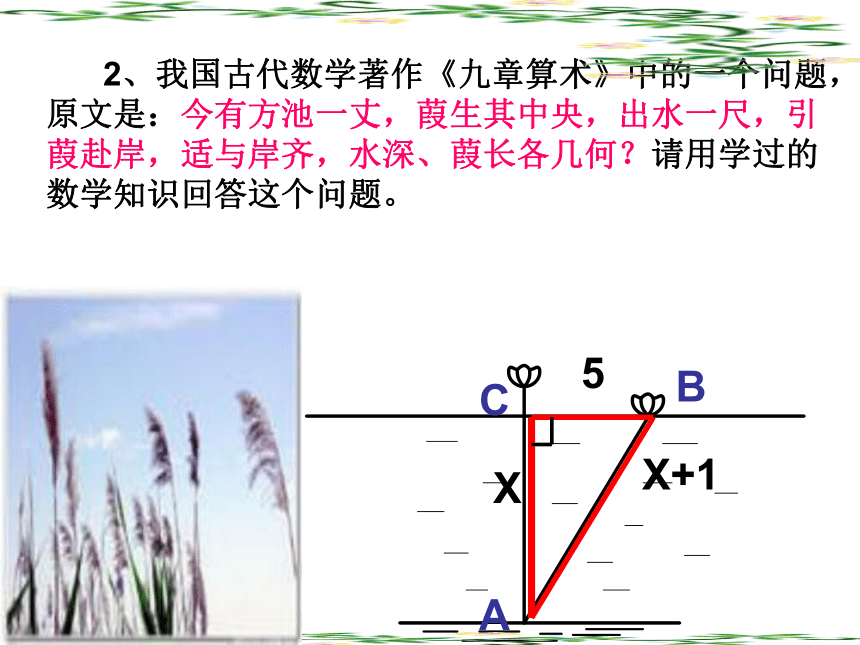
a2 + b2 = c2ABCA的面积+B的面积=C的面积一、分类思想 2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC25或71017817108规律 分类思想 1.直角三角形中,已知两边长,求第三边 时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。二、方程思想1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x +1)米x米2、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
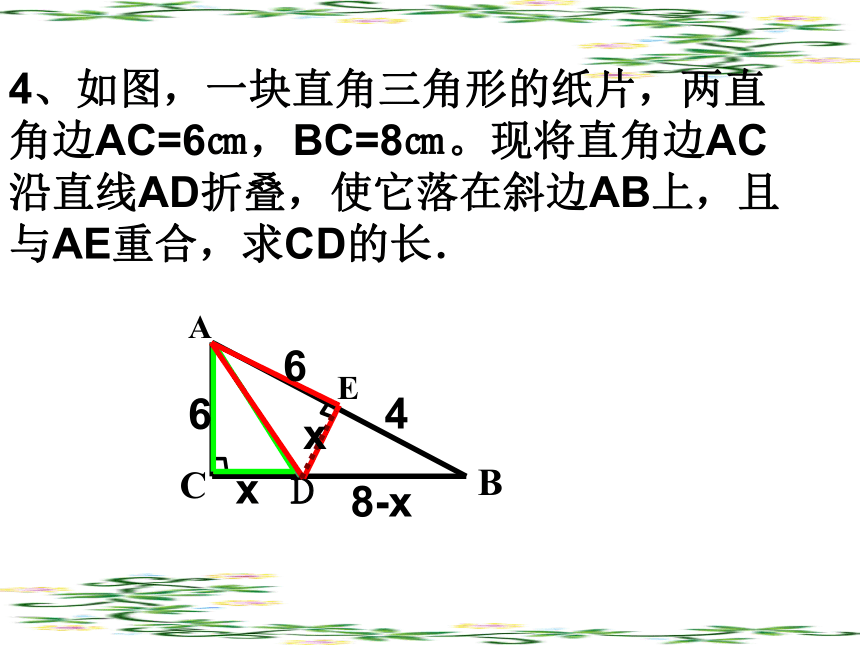
5X+1XCBA4、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长. ACDBE第8题图Dx6x8-x46 方程思想 直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。规律三、展开思想小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC 如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少??
10201020FEAECB2015105 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。 展开思想规律临海中学初二备课组勾股定理复习第二课时一、知识要点如果直角三角形两直角边分别为a,b,斜边为c,
那么勾股定理a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 满足a2 +b2=c2的三个正整数,称为勾股数勾 股 数二、练习(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/13二、练习(二)、选择题1.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25D二、练习
2.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169D二、练习3.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
5.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
A、56 B、48 C、40 D、32DAB二、练习(三)、解答题1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x25-x二、练习3、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x三、小结 本节课主要是应用勾股定理解决实际问题,在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。1.如图所示,这是一块大家常用的一种橡皮,
如果AD=4厘米,CD=3厘米,BC=12厘米,
你能算出AB两点之间的距离吗?随堂练习2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48四、作业勾股定理复习第 三 课 时1. 小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸是(实际测量的误差可不计) A. 9英寸(23厘米) B. 21英寸(54厘米)
C. 29英寸(74厘米) D. 34英寸(87厘米)2.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm3. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )4、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——5、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————6 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
7、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C8、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。9、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?AB82361探索与提高已知直角三角形的两直角边分别长L厘米,M厘米,斜边长N厘米,且L,M,N均为正整数,L为质数.
证明:2(M+L+1)是完全平方数.探索与提高2:如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:ABCACPAC
复习课第一课时勾股定理:如果直角三角形的两直角边分 别为a,b,斜边为c,则有 大正方形的面积可以表示为 —————————— 又可以表示为:———————c2(b-a)2+1/2ab?4
a2 + b2 = c2ABCA的面积+B的面积=C的面积一、分类思想 2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC25或71017817108规律 分类思想 1.直角三角形中,已知两边长,求第三边 时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。二、方程思想1、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(x +1)米x米2、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。
5X+1XCBA4、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长. ACDBE第8题图Dx6x8-x46 方程思想 直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。规律三、展开思想小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC 如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少??
10201020FEAECB2015105 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。 展开思想规律临海中学初二备课组勾股定理复习第二课时一、知识要点如果直角三角形两直角边分别为a,b,斜边为c,
那么勾股定理a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 满足a2 +b2=c2的三个正整数,称为勾股数勾 股 数二、练习(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/13二、练习(二)、选择题1.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
A、25 B、14 C、7 D、7或25D二、练习
2.如果Rt△两直角边的比为5∶12,则斜边上的
高与斜边的比为( )
A、60∶13 B、5∶12
C、12∶13 D、60∶169D二、练习3.如果Rt△的两直角边长分别为n2-1,2n(n>1), 那么它的斜边长是( )
A、2n B、n+1 C、n2-1 D、n2+1
4.已知Rt△ABC中,∠C=90°,若a+b=14cm,
c=10cm,则Rt△ABC的面积是( )
A、24cm2 B、36cm2 C、48cm2 D、60cm2
5.等腰三角形底边上的高为8,周长为32,则三
角形的面积为( )
A、56 B、48 C、40 D、32DAB二、练习(三)、解答题1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x25-x二、练习3、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x三、小结 本节课主要是应用勾股定理解决实际问题,在应用定理时,应注意:1、没有图的要按题意画好图并标上字母;2、不要用错定理。1.如图所示,这是一块大家常用的一种橡皮,
如果AD=4厘米,CD=3厘米,BC=12厘米,
你能算出AB两点之间的距离吗?随堂练习2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48四、作业勾股定理复习第 三 课 时1. 小强量得家里新购置的彩电荧光屏的长为58厘米,宽为46厘米,则这台电视机的尺寸是(实际测量的误差可不计) A. 9英寸(23厘米) B. 21英寸(54厘米)
C. 29英寸(74厘米) D. 34英寸(87厘米)2.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm3. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )4、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——5、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————6 .观察下列表格:……请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
7、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?C8、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。9、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?AB82361探索与提高已知直角三角形的两直角边分别长L厘米,M厘米,斜边长N厘米,且L,M,N均为正整数,L为质数.
证明:2(M+L+1)是完全平方数.探索与提高2:如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:ABCACPAC
