22.2 相似的判定 专题汇总(有答案)
文档属性
| 名称 | 22.2 相似的判定 专题汇总(有答案) | 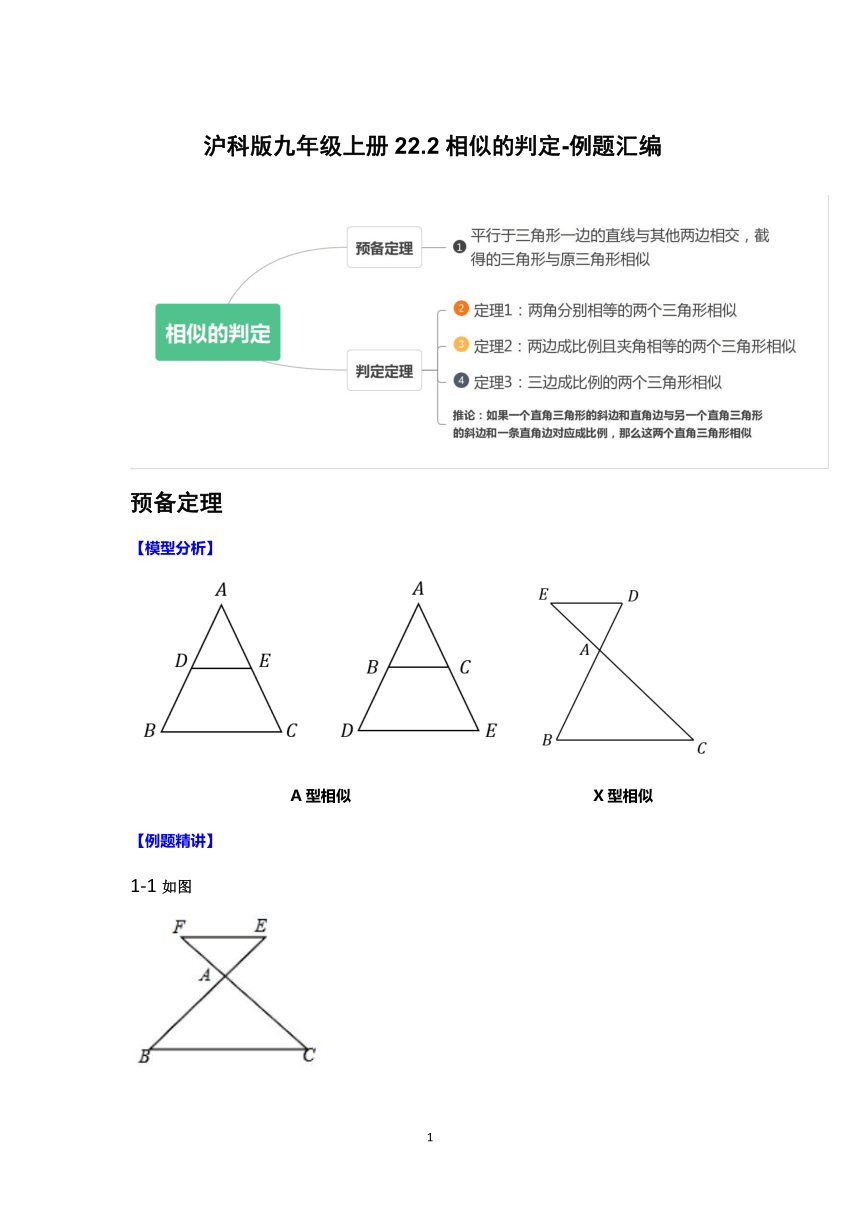 | |
| 格式 | zip | ||
| 文件大小 | 595.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 22:30:57 | ||
图片预览


文档简介
沪科版九年级上册22.2相似的判定-例题汇编
预备定理
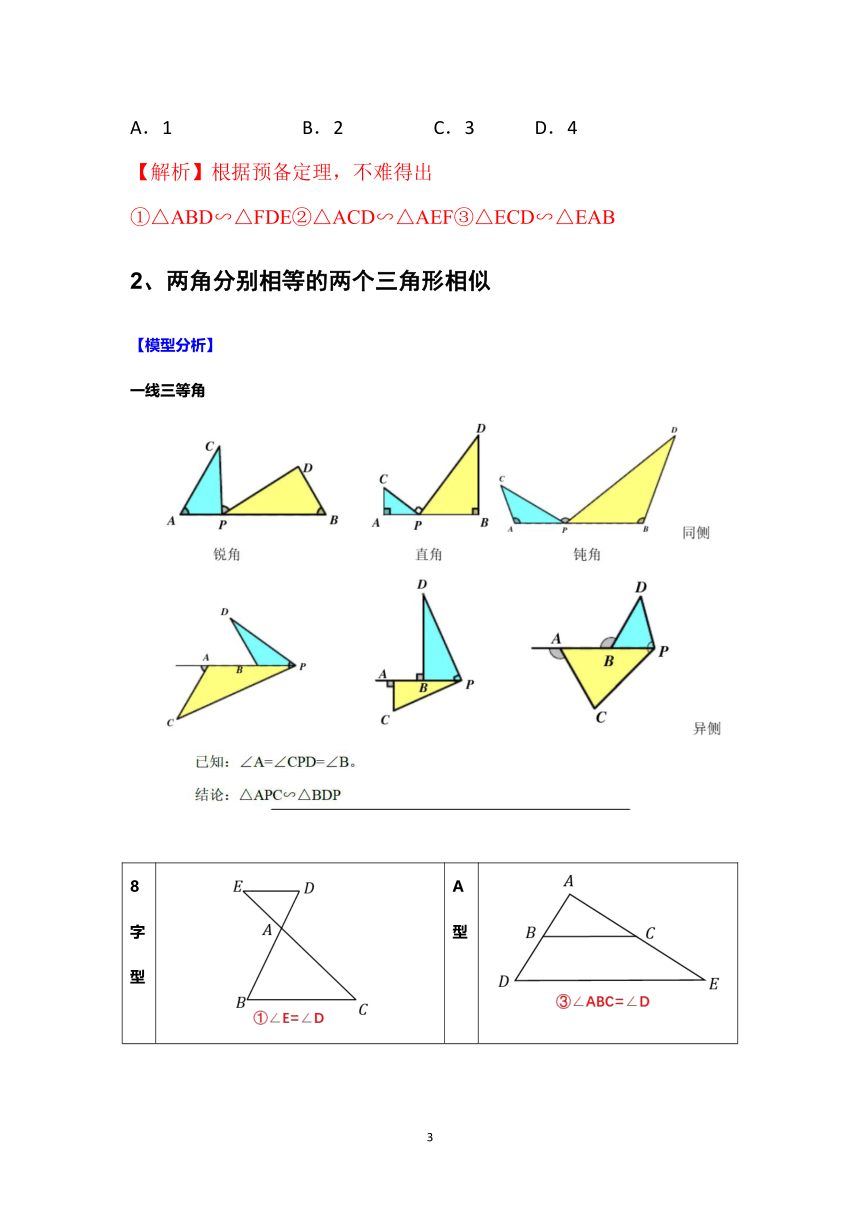
【模型分析】
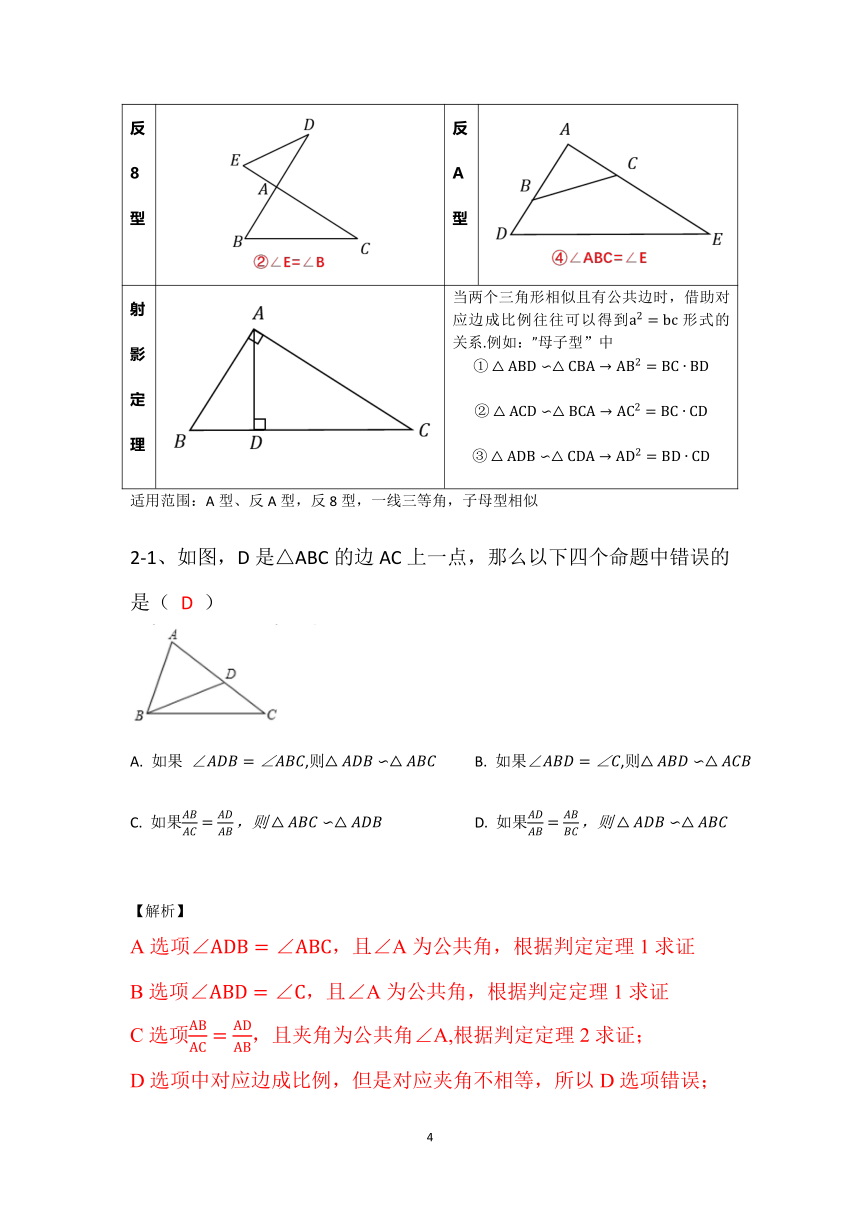
A型相似 X型相似
【例题精讲】
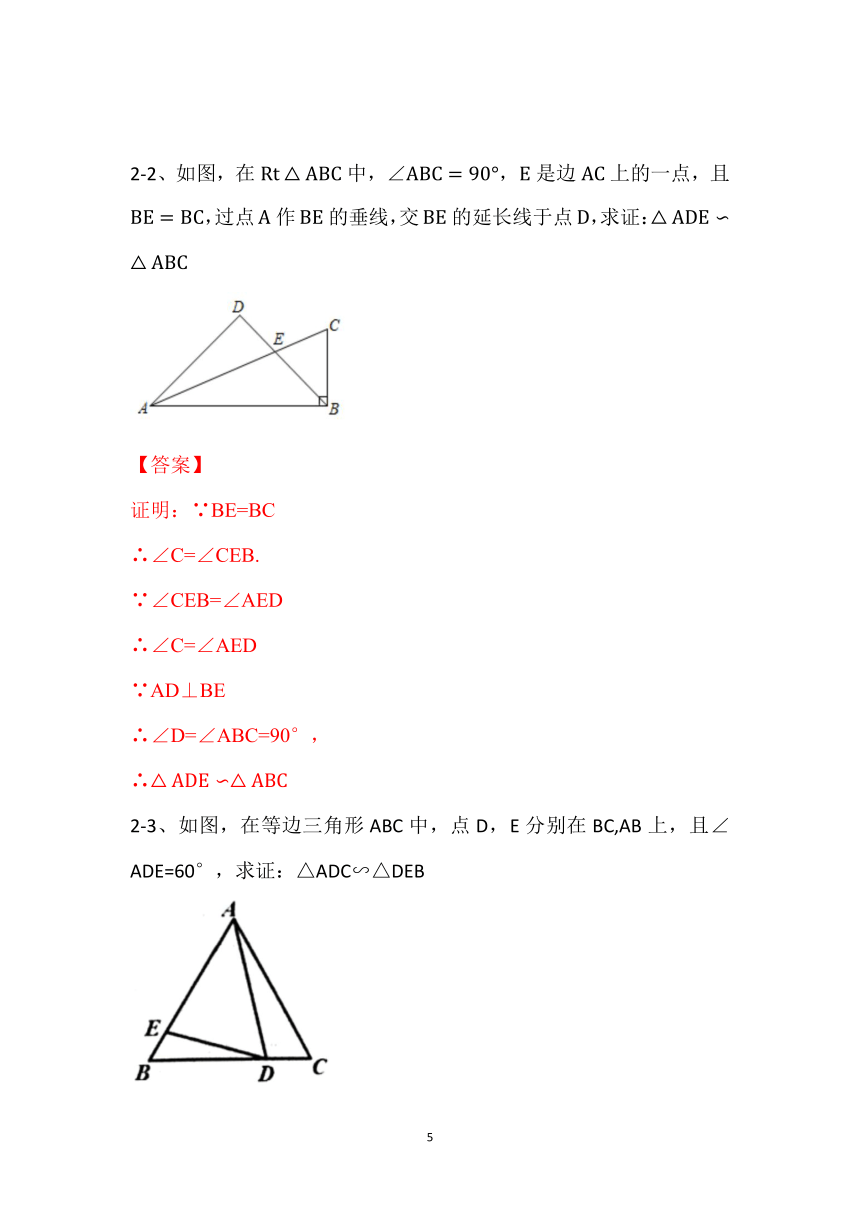
1-1如图
若AE:AB= AB:AC__,则△ABC∽△AEF
若∠E=_∠B_,则△ABC∽△AEF
1-2如图,E是平行四边形ABCD的边BC延长线上的一点,AE交CD于点F,FG//AD交AB于点G.
填空:图中与△CEF相似的三角形有_△BEA,△DAF,_△GFA_;(写出图中与△CEF相似的所有三角形)
从(1)中选出一个三角形,并证明它与△CEF相似。
【答案】△BEA∽△CEF
证明如下:∵四边形ABCD是平行四边形
∴AB//CD
∴∠EFC=∠EAB,∠ECF=∠EBA,∠E=∠E
又∵
∴△BEA∽△CEF
1-3.如图,AB∥CD∥EF,则图中相似的三角形对数为( C )
A.1 B.2 C.3 D.4
【解析】根据预备定理,不难得出
①△ABD∽△FDE②△ACD∽△AEF③△ECD∽△EAB
两角分别相等的两个三角形相似
【模型分析】
一线三等角
8字型 A型
反8型 反A型
射影定理 当两个三角形相似且有公共边时,借助对应边成比例往往可以得到形式的关系.例如:”母子型”中
适用范围:A型、反A型,反8型,一线三等角,子母型相似
2-1、如图,D是△ABC的边AC上一点,那么以下四个命题中错误的是( D )
A. 如果 ∠,则 B. 如果∠,则
C. 如果 D. 如果
【解析】
A选项∠,且∠A为公共角,根据判定定理1求证
B选项∠,且∠A为公共角,根据判定定理1求证
C选项,且夹角为公共角∠A,根据判定定理2求证;
D选项中对应边成比例,但是对应夹角不相等,所以D选项错误;
2-2、如图,在中,是边上的一点,且,过点作的垂线,交的延长线于点,求证:
【答案】
证明:∵BE=BC
∴∠C=∠CEB.
∵∠CEB=∠AED
∴∠C=∠AED
∵AD⊥BE
∴∠D=∠ABC=90°,
∴
2-3、如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°,求证:△ADC∽△DEB
【答案】
证明:△ABC是等边三角形,∴∠B=∠C=60°.
∴∠ADB=∠CAD+∠C=∠CAD+60°.
∵∠ADE=60°,
∴∠ADB=∠BDE+60°
∴∠CAD=∠BDE.
∴△ADC∽△DEB.
2-4、如图,在△ABC中,CD是角平分线,DE平分∠CDB交BC于点E,且DE//AC.
求证:
若,且AC=14,求AD的长
证明 :
是角平分线,
解
平分 ,
,
,
解之 : ,,
,
, ,
,,
,解之: .
3、两边成比例且夹角相等的两个三角形相似
【模型汇总】
使用范围:一线三等角-射影定理,A型反A型相似,母子型相似
3-1、已知在中, 下列阴影部分的三角形与原三角形不相似的是( B )
A. B.
C. D.
【解答】
A、由有两组角对应相等的两个三角形相似,可证阴影部分的三角形与原△ABC相似,故选项A不符合题意;
B、虽有两组边对应成比例,但相等的角不是它们的夹角,所以不能证明阴影部分的三角形与原△ABC相似,故选项B符合题意;
C、由有两组角对应相等的两个三角形相似,可证阴影部分的三角形与原ABC相似,故选项C不符合题意;
D、由两组对应边的比相等且夹角对应相等的两个三角形相似,故选项D不符合题意
3-2、如图,点P在 的边 上,下列条件中不能判断 的是( D )
A. B. C. D.
【解答】
, ,不符合题意;
, ,不符合意;
,即 ,不符合题意;
D. 根据 和 不能判断 ,符合题意 .
故答案为 : D.
3-3如图,在中,点, 分别在边 上, ,线段分别交线段,BC于点,G,且.
(1)求证: ;
(2)若 ,求 的值.
【答案】
证明: ,
(2)解:
,
4、三边成比例且夹角相等的两个三角形相似
4-1.如图所示,在正方形网格中有两个三角形A1B1C1和A2B2C2.求证:△A1B1C1∽△A2B2C2.
【答案】 设网格中每个小正方形的边长均为1.由勾股定理,得A1B1==,A1C1==,A2B2==,B2C2==.又知B1C1=5,A2C2=2,∴==, =,==,∴==,∴△A1B1C1∽△A2B2C2.
4-2如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
解:相似,理由如下:∵=,∴=,又∵==,∴==,∴△ADC∽△A′D′C′,∴∠A=∠A′,又∵=,∴△ABC∽△A′B′C′
4-3如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
【答案】
解:(1)△ACF与△GCA相似.理由:可设正方形ABCD,CDEF,EFGH的边长为a,则△ACF的三边长分别为AC=a,CF=a,AF=a,△GCA的三边长分别为AC=a,CG=2a,AG=a.∴==,==,==.∴==.∴△ACF与△GCA相似.
(2)∵△ACF∽△GCA,∴∠1=∠CAF.∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
预备定理
【模型分析】
A型相似 X型相似
【例题精讲】
1-1如图
若AE:AB= AB:AC__,则△ABC∽△AEF
若∠E=_∠B_,则△ABC∽△AEF
1-2如图,E是平行四边形ABCD的边BC延长线上的一点,AE交CD于点F,FG//AD交AB于点G.
填空:图中与△CEF相似的三角形有_△BEA,△DAF,_△GFA_;(写出图中与△CEF相似的所有三角形)
从(1)中选出一个三角形,并证明它与△CEF相似。
【答案】△BEA∽△CEF
证明如下:∵四边形ABCD是平行四边形
∴AB//CD
∴∠EFC=∠EAB,∠ECF=∠EBA,∠E=∠E
又∵
∴△BEA∽△CEF
1-3.如图,AB∥CD∥EF,则图中相似的三角形对数为( C )
A.1 B.2 C.3 D.4
【解析】根据预备定理,不难得出
①△ABD∽△FDE②△ACD∽△AEF③△ECD∽△EAB
两角分别相等的两个三角形相似
【模型分析】
一线三等角
8字型 A型
反8型 反A型
射影定理 当两个三角形相似且有公共边时,借助对应边成比例往往可以得到形式的关系.例如:”母子型”中
适用范围:A型、反A型,反8型,一线三等角,子母型相似
2-1、如图,D是△ABC的边AC上一点,那么以下四个命题中错误的是( D )
A. 如果 ∠,则 B. 如果∠,则
C. 如果 D. 如果
【解析】
A选项∠,且∠A为公共角,根据判定定理1求证
B选项∠,且∠A为公共角,根据判定定理1求证
C选项,且夹角为公共角∠A,根据判定定理2求证;
D选项中对应边成比例,但是对应夹角不相等,所以D选项错误;
2-2、如图,在中,是边上的一点,且,过点作的垂线,交的延长线于点,求证:
【答案】
证明:∵BE=BC
∴∠C=∠CEB.
∵∠CEB=∠AED
∴∠C=∠AED
∵AD⊥BE
∴∠D=∠ABC=90°,
∴
2-3、如图,在等边三角形ABC中,点D,E分别在BC,AB上,且∠ADE=60°,求证:△ADC∽△DEB
【答案】
证明:△ABC是等边三角形,∴∠B=∠C=60°.
∴∠ADB=∠CAD+∠C=∠CAD+60°.
∵∠ADE=60°,
∴∠ADB=∠BDE+60°
∴∠CAD=∠BDE.
∴△ADC∽△DEB.
2-4、如图,在△ABC中,CD是角平分线,DE平分∠CDB交BC于点E,且DE//AC.
求证:
若,且AC=14,求AD的长
证明 :
是角平分线,
解
平分 ,
,
,
解之 : ,,
,
, ,
,,
,解之: .
3、两边成比例且夹角相等的两个三角形相似
【模型汇总】
使用范围:一线三等角-射影定理,A型反A型相似,母子型相似
3-1、已知在中, 下列阴影部分的三角形与原三角形不相似的是( B )
A. B.
C. D.
【解答】
A、由有两组角对应相等的两个三角形相似,可证阴影部分的三角形与原△ABC相似,故选项A不符合题意;
B、虽有两组边对应成比例,但相等的角不是它们的夹角,所以不能证明阴影部分的三角形与原△ABC相似,故选项B符合题意;
C、由有两组角对应相等的两个三角形相似,可证阴影部分的三角形与原ABC相似,故选项C不符合题意;
D、由两组对应边的比相等且夹角对应相等的两个三角形相似,故选项D不符合题意
3-2、如图,点P在 的边 上,下列条件中不能判断 的是( D )
A. B. C. D.
【解答】
, ,不符合题意;
, ,不符合意;
,即 ,不符合题意;
D. 根据 和 不能判断 ,符合题意 .
故答案为 : D.
3-3如图,在中,点, 分别在边 上, ,线段分别交线段,BC于点,G,且.
(1)求证: ;
(2)若 ,求 的值.
【答案】
证明: ,
(2)解:
,
4、三边成比例且夹角相等的两个三角形相似
4-1.如图所示,在正方形网格中有两个三角形A1B1C1和A2B2C2.求证:△A1B1C1∽△A2B2C2.
【答案】 设网格中每个小正方形的边长均为1.由勾股定理,得A1B1==,A1C1==,A2B2==,B2C2==.又知B1C1=5,A2C2=2,∴==, =,==,∴==,∴△A1B1C1∽△A2B2C2.
4-2如图,在△ABC和△A′B′C′中,D,D′分别是AB,A′B′上一点,=.当==时,判断△ABC与△A′B′C′是否相似,并说明理由.
解:相似,理由如下:∵=,∴=,又∵==,∴==,∴△ADC∽△A′D′C′,∴∠A=∠A′,又∵=,∴△ABC∽△A′B′C′
4-3如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
【答案】
解:(1)△ACF与△GCA相似.理由:可设正方形ABCD,CDEF,EFGH的边长为a,则△ACF的三边长分别为AC=a,CF=a,AF=a,△GCA的三边长分别为AC=a,CG=2a,AG=a.∴==,==,==.∴==.∴△ACF与△GCA相似.
(2)∵△ACF∽△GCA,∴∠1=∠CAF.∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
