勾股定理复习[下学期]
图片预览





文档简介
课件29张PPT。勾股定理复习1.直角三角形的边、角之间分别存在什么关系?⑴角与角之间的关系:
在△ABC中,∠C=90o,有∠A+∠B=90o
⑵边与边之间的关系:
在△ABC中,∠C=90o,有
议一议:2、如何判断一个三角形是直角三角形。在△ABC中,
①如果∠A+∠B=90o,则 △ABC是直角三角形;
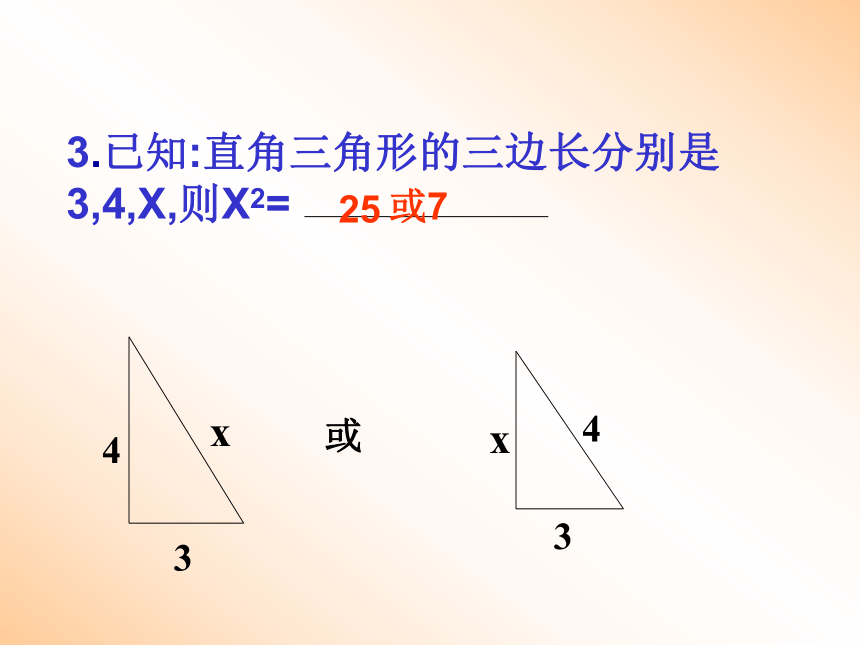
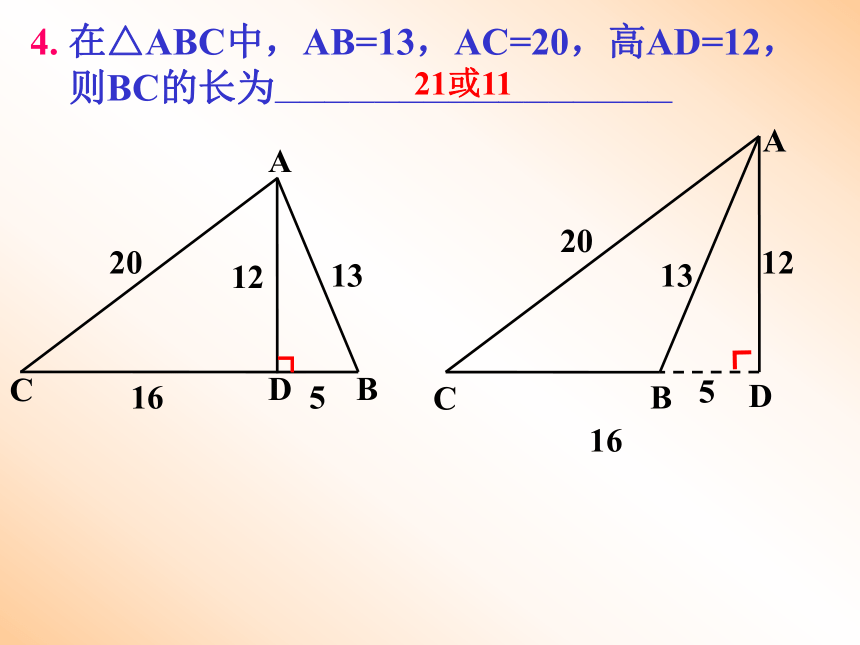
②如果 ,则 △ABC是直角三角形 2、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是___1.一个直角三角形的三边长是连续整数,则面积是___填空题3,4,566,8,102425或7或4. 在△ABC中,AB=13,AC=20,高AD=12,
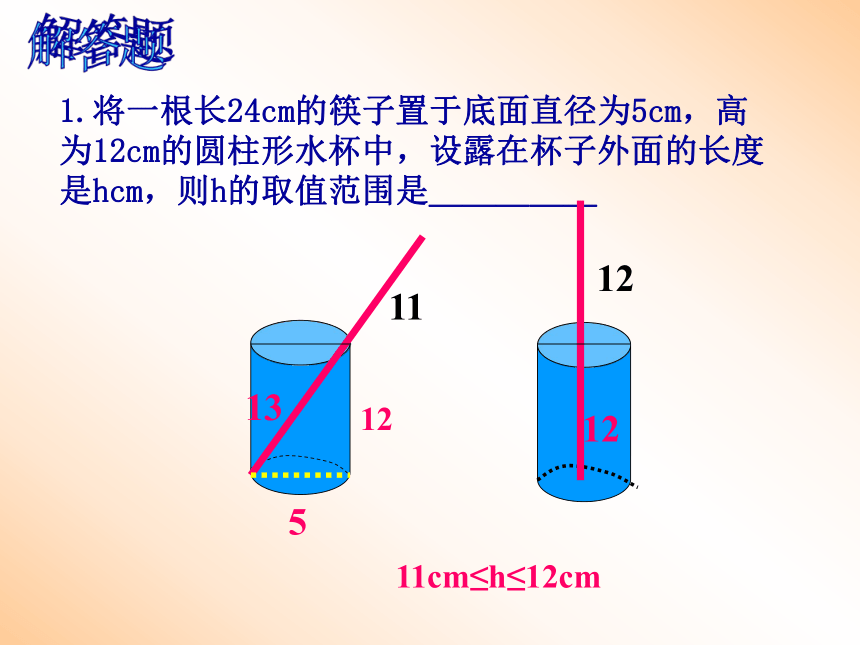
则BC的长为————————————————16551621或11 这种解题思想叫分类思想 1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。归纳:1.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,设露在杯子外面的长度是hcm,则h的取值范围是_____
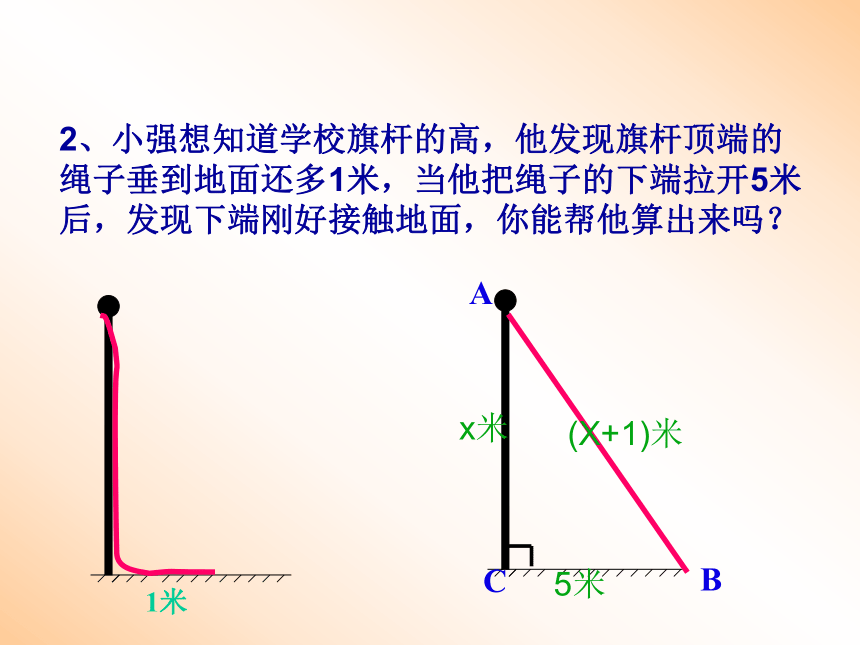
51213111212解答题11cm≤h≤12cm2、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(X+1)米x米1米3、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。译:有一个水池,水面是一个为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。这个水池的 深度与这根芦苇的长度分别是多少?1xX+154、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长. ACDBE第8题图Dx6x8-x4685.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8cm,BC=10cm求(1)CF(2)EC
ABCD864X10108-X8-XEF1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
做一做:解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x25-x2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=483、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x 这种解题思想叫方程思想 直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。归纳:小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC 如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少??
10201020FEAECB2015105 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。 展开思想规律你会求三角形的面积吗?1.在三角形ABC中, AB=15 , BC=14 , AC=13,
求三角形ABC的面积.DX14-X 2、等腰直角三角形的斜边为6cm,则它的面积是_____3、Rt△ABC中,∠C=90°,若a+b=7cm,c=5cm,则此三角形的面积是____4、已知直角三角形的斜边长为2,周长为2+√6,则这个三角形的面积为___5、等腰三角形的底边上的高为4,周长为16,则三角形的面积是____休息一下
在△ABC中,∠C=90o,有∠A+∠B=90o
⑵边与边之间的关系:
在△ABC中,∠C=90o,有
议一议:2、如何判断一个三角形是直角三角形。在△ABC中,
①如果∠A+∠B=90o,则 △ABC是直角三角形;
②如果 ,则 △ABC是直角三角形 2、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是___1.一个直角三角形的三边长是连续整数,则面积是___填空题3,4,566,8,102425或7或4. 在△ABC中,AB=13,AC=20,高AD=12,
则BC的长为————————————————16551621或11 这种解题思想叫分类思想 1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。 2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。归纳:1.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,设露在杯子外面的长度是hcm,则h的取值范围是_____
51213111212解答题11cm≤h≤12cm2、小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗? ABC5米(X+1)米x米1米3、我国古代数学著作《九章算术》中的一个问题,原文是:今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,水深、葭长各几何?请用学过的数学知识回答这个问题。译:有一个水池,水面是一个为10尺的正方形,在水池正中央有一根芦苇,它高出水面一尺。如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面。这个水池的 深度与这根芦苇的长度分别是多少?1xX+154、如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长. ACDBE第8题图Dx6x8-x4685.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8cm,BC=10cm求(1)CF(2)EC
ABCD864X10108-X8-XEF1、如图,铁路上A,B两点相距25km,C,D为
两村庄,DA⊥AB于A,CB⊥AB于B,已知
DA=15km,CB=10km,现在要在铁路AB上
建一个土特产品收购站E,使得C,D两村到
E站的距离相等,则E站应建在离A站多少km
处?
做一做:解:设AE= x km,则 BE=(25-x)km
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
∴ x=10
答:E站应建在离A站10km处。
x25-x2、等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为X,则AB为(16-X), 由勾股定理得:
X2+82=(16-X)2即X2+64=256-32X+X2∴ X=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=483、已知,如图,在Rt△ABC中,∠C=90°,
∠1=∠2,CD=1.5, BD=2.5, 求AC的长.提示:作辅助线DE⊥AB,利用平分线的性质和勾股定理。解:过D点做DE⊥ABE∵ ∠1=∠2, ∠C=90°
∴ DE=CD=1.5
在 Rt△DEB中,根据勾股定理,得
BE2=BD2-DE2=2.52-1.52=4 ∴ BE=2
在Rt△ACD和 Rt△AED中,
∵CD=DE , AD=AD ∴ Rt△ACD Rt△AED
∴ AC=AE
令AC=x,则AB=x+2
在 Rt△ABC中,根据勾股定理,得 AC2+BC2=AB2
即:x2+42=(x+2)2 ∴ x=3x 这种解题思想叫方程思想 直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。归纳:小明家住在18层的高楼,一天,他与妈妈去买竹竿。买最长的吧!快点回家,好用它凉衣服。糟糕,太长了,放不进去。如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?xX2=1.52+1.52=4.5AB2=2.22+X2=9.34AB≈3米如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,
A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿
着台阶面爬到B点最短路程是多少?
20232323ABC 如图,长方体的长为15 cm,宽为 10 cm,高为20 cm,点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B,需要爬行的最短距离是多少??
10201020FEAECB2015105 1. 几何体的表面路径最短的问题,一般展开表面成平面。 2.利用两点之间线段最短,及勾股定理求解。 展开思想规律你会求三角形的面积吗?1.在三角形ABC中, AB=15 , BC=14 , AC=13,
求三角形ABC的面积.DX14-X 2、等腰直角三角形的斜边为6cm,则它的面积是_____3、Rt△ABC中,∠C=90°,若a+b=7cm,c=5cm,则此三角形的面积是____4、已知直角三角形的斜边长为2,周长为2+√6,则这个三角形的面积为___5、等腰三角形的底边上的高为4,周长为16,则三角形的面积是____休息一下
