24.1 锐角三角函数(2)课件
图片预览



文档简介
课件15张PPT。沪科版九年级数学(上册)第二十四章
用数学视觉观察世界
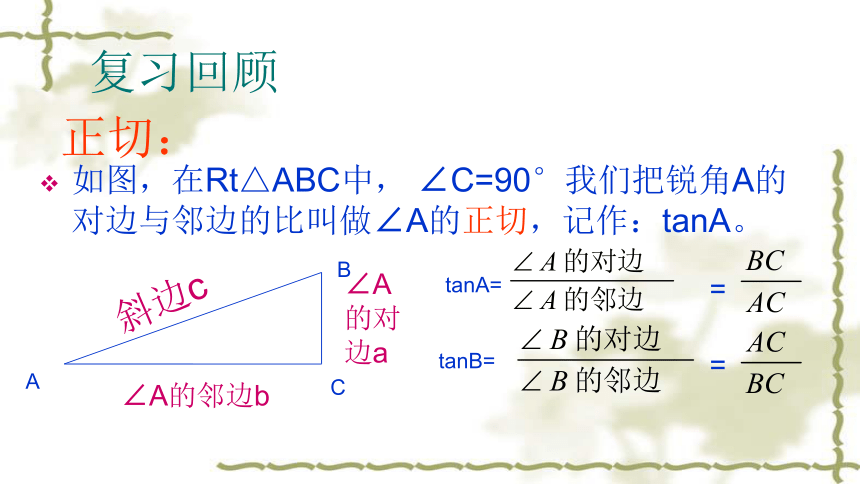
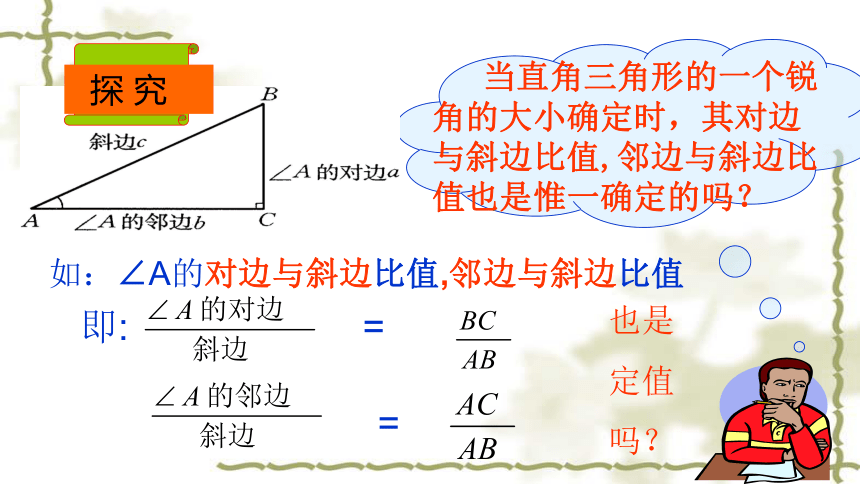
用数学思维思考世界24.1锐角三角函数(第二课时)复习回顾如图,在Rt△ABC中, ∠C=90°我们把锐角A的对边与邻边的比叫做∠A的正切,记作:tanA。正切:tanA==tanB==也是
定值
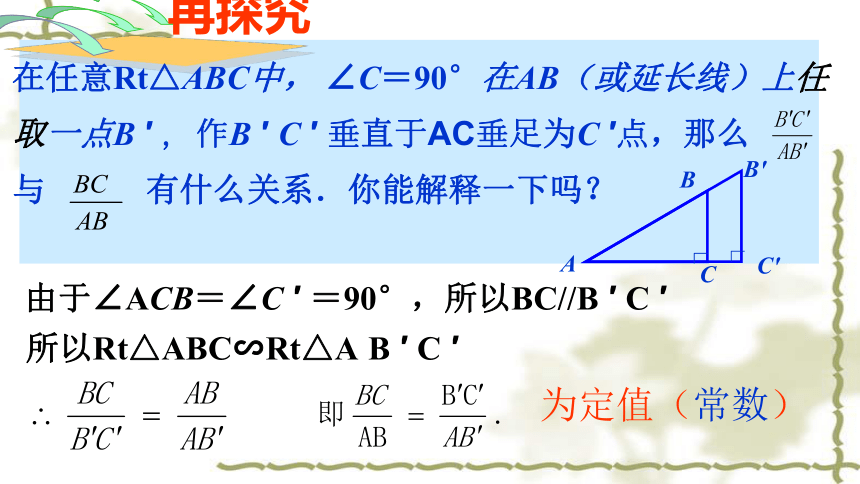
吗?再探究BCAB'C'由于∠ACB=∠C ′ =90°,所以BC//B ′ C ′
所以Rt△ABC∽Rt△A B ′ C ′为定值(常数) 在直角三角形中,锐角A的对边与斜边的比
叫做角A的正弦,记作: sinA类似地可以证明:在有一个锐角A的直角三角形中,角A的邻边与斜边的比值也为一个常数。在直角三角形中,锐角A的邻边与斜边的比
叫做角A的余弦,记作:cosA 锐角A的正弦、
余弦、正切都叫做
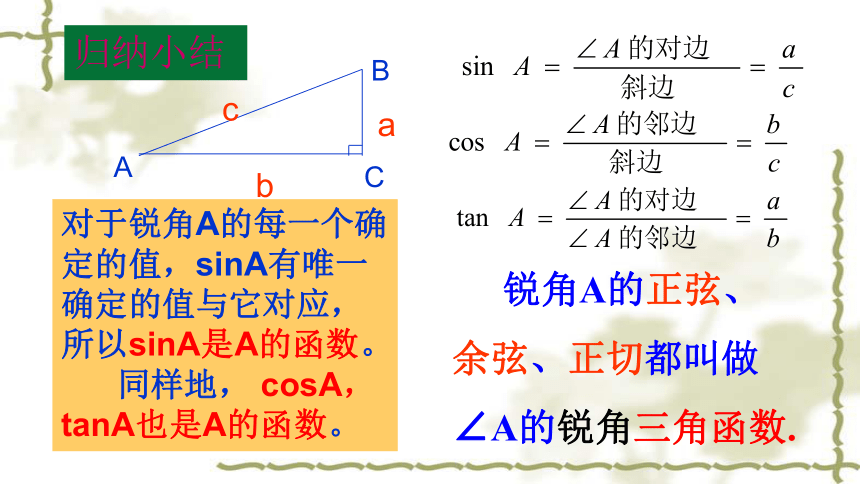
∠A的锐角三角函数.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。
同样地, cosA,tanA也是A的函数。BACabc归纳小结(1)求∠A的正弦sinA ;
(2)求∠A的余弦cosA . (1) ∠A的对边BC=3m,斜边
AB=5m.于是(2) ∠A的邻边是AC.根据勾股定理,得于是 AC=4m.因此思考求∠B的正弦sinB和cosB的值在直角三角形ABC中, ∠C= 90o,
BC:AC = 3 :4.A ∠A的对边为BC=3k,斜边AB=5k.于是求∠A的正弦sinA 余弦cosA .因为 BC:AC=3:4,∠A的邻边是AC=4k.于是拓展延伸设BC=3k,AC=4k,根据勾股定理,得:AB=5k.方法点拨:参数法(参数为k)试一试在直角三角形ABC中, ∠C= 90o, ∠A= 30o求∠A的正弦sinA ;
∠A的余弦cosA .CBA30°Rt△ABC中, ∠C= 90o, ∠A= 30o 由于在直角三角形中, 30o所对的直角边等于斜边的一半,得:AB=2BC,即AB:BC=2:1设:BC=k,AB=2k根据勾股定理,得:AC=所以如图平面直角坐标系中,点P的坐标为(3,4),
求OP与x轴正半轴夹角α的所有三角函数值。αyP(3,4)xO过P作PQ ⊥x轴于Q点,在Rt△POQ中,OQ=3,QP=4 所以OP=5所以构造三直角角形思路点拨:展示你的风采1. 求直线y=2x与x轴正半轴夹角α的所有三角函数值。oxyy=2x在y=2x上任取一点P(1,2),过P作PQ ⊥x轴于Q点,在Rt△POQ中,OQ=1,QP=2 所以OP=所以α在直角三角形中,∠A为其中一个锐角这节课我们主要学习了哪些知识?有何体会和收获?有哪些你认为最重要?tan A =其中sinA , cosA,tanA是角A的函数。定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 作 业课本P107 练习1,2.
发散思维
1、在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB.结 束 语 学习任何东西,
最好的途径是自己去发现!同学们,再见
用数学思维思考世界24.1锐角三角函数(第二课时)复习回顾如图,在Rt△ABC中, ∠C=90°我们把锐角A的对边与邻边的比叫做∠A的正切,记作:tanA。正切:tanA==tanB==也是
定值
吗?再探究BCAB'C'由于∠ACB=∠C ′ =90°,所以BC//B ′ C ′
所以Rt△ABC∽Rt△A B ′ C ′为定值(常数) 在直角三角形中,锐角A的对边与斜边的比
叫做角A的正弦,记作: sinA类似地可以证明:在有一个锐角A的直角三角形中,角A的邻边与斜边的比值也为一个常数。在直角三角形中,锐角A的邻边与斜边的比
叫做角A的余弦,记作:cosA 锐角A的正弦、
余弦、正切都叫做
∠A的锐角三角函数.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数。
同样地, cosA,tanA也是A的函数。BACabc归纳小结(1)求∠A的正弦sinA ;
(2)求∠A的余弦cosA . (1) ∠A的对边BC=3m,斜边
AB=5m.于是(2) ∠A的邻边是AC.根据勾股定理,得于是 AC=4m.因此思考求∠B的正弦sinB和cosB的值在直角三角形ABC中, ∠C= 90o,
BC:AC = 3 :4.A ∠A的对边为BC=3k,斜边AB=5k.于是求∠A的正弦sinA 余弦cosA .因为 BC:AC=3:4,∠A的邻边是AC=4k.于是拓展延伸设BC=3k,AC=4k,根据勾股定理,得:AB=5k.方法点拨:参数法(参数为k)试一试在直角三角形ABC中, ∠C= 90o, ∠A= 30o求∠A的正弦sinA ;
∠A的余弦cosA .CBA30°Rt△ABC中, ∠C= 90o, ∠A= 30o 由于在直角三角形中, 30o所对的直角边等于斜边的一半,得:AB=2BC,即AB:BC=2:1设:BC=k,AB=2k根据勾股定理,得:AC=所以如图平面直角坐标系中,点P的坐标为(3,4),
求OP与x轴正半轴夹角α的所有三角函数值。αyP(3,4)xO过P作PQ ⊥x轴于Q点,在Rt△POQ中,OQ=3,QP=4 所以OP=5所以构造三直角角形思路点拨:展示你的风采1. 求直线y=2x与x轴正半轴夹角α的所有三角函数值。oxyy=2x在y=2x上任取一点P(1,2),过P作PQ ⊥x轴于Q点,在Rt△POQ中,OQ=1,QP=2 所以OP=所以α在直角三角形中,∠A为其中一个锐角这节课我们主要学习了哪些知识?有何体会和收获?有哪些你认为最重要?tan A =其中sinA , cosA,tanA是角A的函数。定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。 作 业课本P107 练习1,2.
发散思维
1、在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB.结 束 语 学习任何东西,
最好的途径是自己去发现!同学们,再见
