冀教版数学七年级上册3.2代数式限时作业(含答案)
文档属性
| 名称 | 冀教版数学七年级上册3.2代数式限时作业(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 00:00:00 | ||
图片预览


文档简介
3.2代数式限时作业冀教版数学七年级上册
(限时60分钟,满分120分)
一、单选题(共10题;共30分)
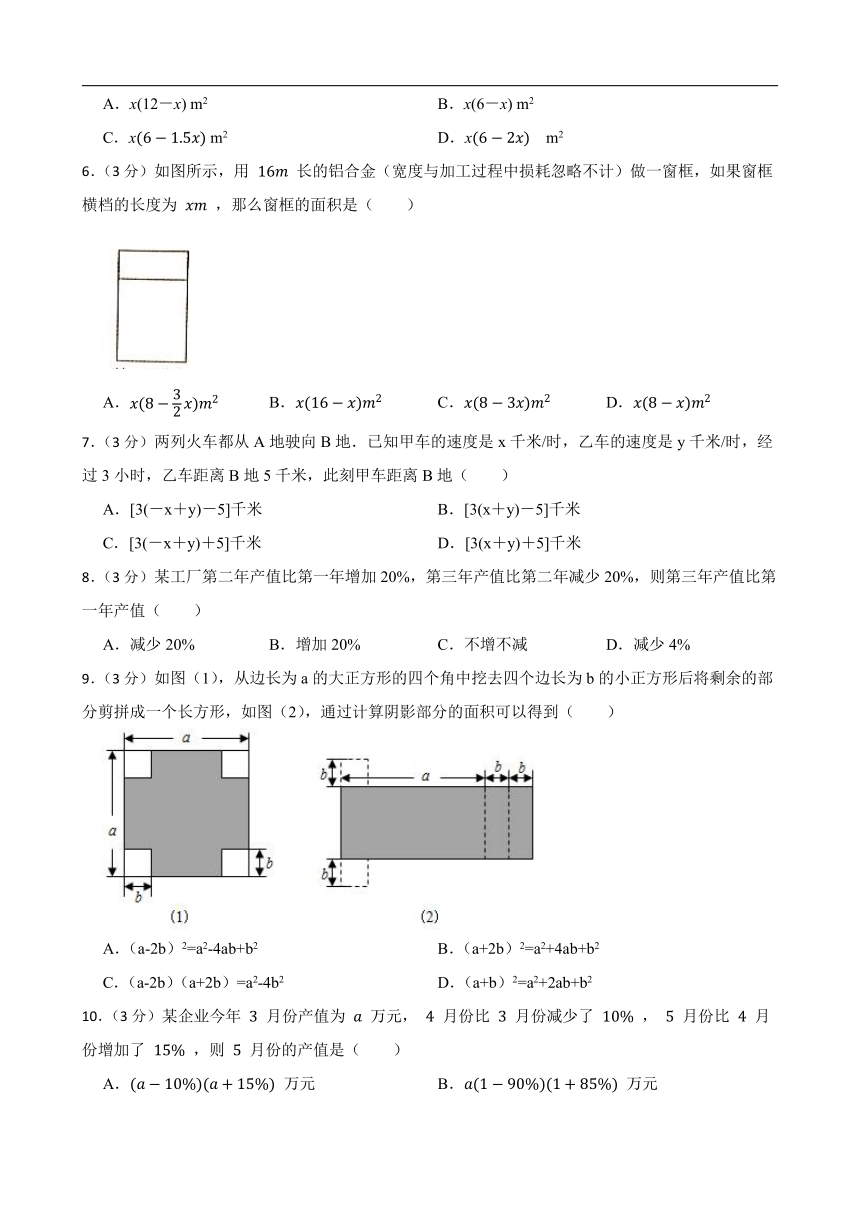
1.(3分)如图,设k= (a>b>0),则有( )
A.02.(3分)某件商品9折降价销售后每件商品售价为a元,则该商品每件原价( )
A.0.92a B.1.12a C. D.
3.(3分)张老板以每颗a元的单价买进水蜜桃100颗.现以每颗比单价多两成的价格卖出70颗后,再以每颗比单价低b元的价格将剩下的30颗卖出,则全部水蜜桃共卖( )
A.70a+30(a-b)
B.70×(1+20%)×a+30
C.100×(1+20%)×a-30(a-b)
D.70×(1+20%)×a+30(a-b)
4.(3分)如图所示,在第一个正方形上加放一根小棒,在此基础上依次加搭正方形,连同第一个在内,共搭了101个正方形,则需要的小棒根数是( )
A.4+101×3 B.4+100×3 C.5+101×3 D.5+100×3
5.(3分)用12m长的铝合金做成一个长方形的窗框(如图),设长方形窗框横条的长度为x(m),则长方形窗框的面积为( )
A.x(12-x) m2 B.x(6-x) m2
C.x m2 D.x m2
6.(3分)如图所示,用 长的铝合金(宽度与加工过程中损耗忽略不计)做一窗框,如果窗框横档的长度为 ,那么窗框的面积是( )
A. B. C. D.
7.(3分)两列火车都从A地驶向B地.已知甲车的速度是x千米/时,乙车的速度是y千米/时,经过3小时,乙车距离B地5千米,此刻甲车距离B地( )
A.[3(-x+y)-5]千米 B.[3(x+y)-5]千米
C.[3(-x+y)+5]千米 D.[3(x+y)+5]千米
8.(3分)某工厂第二年产值比第一年增加20%,第三年产值比第二年减少20%,则第三年产值比第一年产值( )
A.减少20% B.增加20% C.不增不减 D.减少4%
9.(3分)如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a-2b)2=a2-4ab+b2 B.(a+2b)2=a2+4ab+b2
C.(a-2b)(a+2b)=a2-4b2 D.(a+b)2=a2+2ab+b2
10.(3分)某企业今年 月份产值为 万元, 月份比 月份减少了 , 月份比 月份增加了 ,则 月份的产值是( )
A. 万元 B. 万元
C. 万元 D. 万元
二、填空题(共10题;共30分)
11.(3分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“ ”的图案,如图2所示,则这个“ ”图案的周长可表示为 .
12.(3分)某地居民用电收费标准为:每月如果不超过100度,那么每度按a元收费,如果超过100度,超出部分每度按b元收费,某户居民一个月用电160度,该户居民这个月应交电费 元( 用含a,b的式子表示).
13.(3分)每件a元的上衣先提价10%,再打九折以后出售的价格是 元/件;
14.(3分)某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为 元.
15.(3分)x的10%与y的差比y的2倍少3,列方程为 .
16.(3分)某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为 .
17.(3分)通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是 元.
18.(3分)一个长方体的长、宽、高分别是a、b、c,则这个长方体的表面积是 ;
19.(3分)某校组织师生去天童山进行社会实践活动.若学校租用30座的客车 辆,则有15人无法乘坐;若租用45座的客车则可少租用2辆,且最后一辆车还没坐满.那么乘坐最后一辆45座客车的人数是 人(用含 的代数式表示).
20.(3分)一个两位数,个位数字是十位数字的2倍,若个位数字为a,则这个两位数可表示为
三、解答题(共5题;共60分)
21.(10分)如图,是一所小区前的一块长方形空地,在空地中规划建设一个长方形和半圆的建筑物,其余部分进行绿化,用式子表示这块空地的绿化面积.
22.(10分)小丁和小亮一起去吃冰糕,小丁花了m元,小亮花了n元,已知每个冰糕0.5元,小丁和小亮各吃了几个?
23.(10分)康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:
甲地(元/台) 乙地(元/台)
A地 600 500
B地 400 800
从A地运往甲地x台,总费用多少元?(用含x的代数式表示)
24.(15分)如图所示,较大的半圆半径 ,较小的半圆半径 ,求阴影部分的周长 和面积 .(π取3.14)
25.(15分)为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)(5分)求每套队服和每个足球的价格是多少?
(2)(5分)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)(5分)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
答案部分
1.D
2.C
3.D
4.D
5.C
6.A
7.C
8.D
9.C
10.C
11.8a-4b
12.100a +60b
13.0.99a
14.1.08a
15.10%x﹣y=2y﹣3
16.或
17.(a+1.25b)
18.2ab+2ac+2bc
19.
20.6a
21.解:这块空地的绿化面积为: ,
答:这块空地的绿化面积是
22.解:已知每个冰糕0.5元,小丁花了m元,则小丁吃的个数为: ;小亮花了n元,小亮吃的个数为:
23.解:∵从A地运往甲地x台,A地有机器17台,
∴从A地运往乙地(17﹣x)台,
∵甲地需要18台,
∴从B地运往甲地(18﹣x)台,
∵乙地需要14台,
∴B往乙地运14﹣(17﹣x)=x﹣3,
∴总费用=600x+500×(17﹣x)+400×(18﹣x)+800×(x﹣3)=500x+13300.(3≤x≤17,且x为整数).
24.解:阴影部分的周长:
2×3.14×5÷2+2×3.14×3÷2+(5×2-3×2)
=15.7+9.42+4
=29.12;
阴影部分的面积:
3.14×52÷2-3.14×32÷2
=39.25-14.13
=25.12;
答:阴影部分的周长C阴影是29.12,面积S阴影是25.12.
25.(1)解:设每个足球的定价是x元,则每套队服是(x+50)元,根据题意得
2(x+50)=3x,
解得x=100,
x+50=150.
答:每套队服150元,每个足球100元。
(2)解:到甲商场购买所花的费用为:150×100+100(a﹣ )=100a+14000(元),
到乙商场购买所花的费用为:150×100+0.8×100 a=80a+15000(元)
(3)解:当在两家商场购买一样合算时,100a+14000=80a+15000,解得a=50.
所以购买的足球数等于50个时,则在两家商场购买一样合算;
购买的足球数多于50个时,则到乙商场购买合算;
购买的足球数少于50个时,则到甲商场购买合算
(限时60分钟,满分120分)
一、单选题(共10题;共30分)
1.(3分)如图,设k= (a>b>0),则有( )
A.0
A.0.92a B.1.12a C. D.
3.(3分)张老板以每颗a元的单价买进水蜜桃100颗.现以每颗比单价多两成的价格卖出70颗后,再以每颗比单价低b元的价格将剩下的30颗卖出,则全部水蜜桃共卖( )
A.70a+30(a-b)
B.70×(1+20%)×a+30
C.100×(1+20%)×a-30(a-b)
D.70×(1+20%)×a+30(a-b)
4.(3分)如图所示,在第一个正方形上加放一根小棒,在此基础上依次加搭正方形,连同第一个在内,共搭了101个正方形,则需要的小棒根数是( )
A.4+101×3 B.4+100×3 C.5+101×3 D.5+100×3
5.(3分)用12m长的铝合金做成一个长方形的窗框(如图),设长方形窗框横条的长度为x(m),则长方形窗框的面积为( )
A.x(12-x) m2 B.x(6-x) m2
C.x m2 D.x m2
6.(3分)如图所示,用 长的铝合金(宽度与加工过程中损耗忽略不计)做一窗框,如果窗框横档的长度为 ,那么窗框的面积是( )
A. B. C. D.
7.(3分)两列火车都从A地驶向B地.已知甲车的速度是x千米/时,乙车的速度是y千米/时,经过3小时,乙车距离B地5千米,此刻甲车距离B地( )
A.[3(-x+y)-5]千米 B.[3(x+y)-5]千米
C.[3(-x+y)+5]千米 D.[3(x+y)+5]千米
8.(3分)某工厂第二年产值比第一年增加20%,第三年产值比第二年减少20%,则第三年产值比第一年产值( )
A.减少20% B.增加20% C.不增不减 D.减少4%
9.(3分)如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A.(a-2b)2=a2-4ab+b2 B.(a+2b)2=a2+4ab+b2
C.(a-2b)(a+2b)=a2-4b2 D.(a+b)2=a2+2ab+b2
10.(3分)某企业今年 月份产值为 万元, 月份比 月份减少了 , 月份比 月份增加了 ,则 月份的产值是( )
A. 万元 B. 万元
C. 万元 D. 万元
二、填空题(共10题;共30分)
11.(3分)如图1,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“ ”的图案,如图2所示,则这个“ ”图案的周长可表示为 .
12.(3分)某地居民用电收费标准为:每月如果不超过100度,那么每度按a元收费,如果超过100度,超出部分每度按b元收费,某户居民一个月用电160度,该户居民这个月应交电费 元( 用含a,b的式子表示).
13.(3分)每件a元的上衣先提价10%,再打九折以后出售的价格是 元/件;
14.(3分)某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为 元.
15.(3分)x的10%与y的差比y的2倍少3,列方程为 .
16.(3分)某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为 .
17.(3分)通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是 元.
18.(3分)一个长方体的长、宽、高分别是a、b、c,则这个长方体的表面积是 ;
19.(3分)某校组织师生去天童山进行社会实践活动.若学校租用30座的客车 辆,则有15人无法乘坐;若租用45座的客车则可少租用2辆,且最后一辆车还没坐满.那么乘坐最后一辆45座客车的人数是 人(用含 的代数式表示).
20.(3分)一个两位数,个位数字是十位数字的2倍,若个位数字为a,则这个两位数可表示为
三、解答题(共5题;共60分)
21.(10分)如图,是一所小区前的一块长方形空地,在空地中规划建设一个长方形和半圆的建筑物,其余部分进行绿化,用式子表示这块空地的绿化面积.
22.(10分)小丁和小亮一起去吃冰糕,小丁花了m元,小亮花了n元,已知每个冰糕0.5元,小丁和小亮各吃了几个?
23.(10分)康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:
甲地(元/台) 乙地(元/台)
A地 600 500
B地 400 800
从A地运往甲地x台,总费用多少元?(用含x的代数式表示)
24.(15分)如图所示,较大的半圆半径 ,较小的半圆半径 ,求阴影部分的周长 和面积 .(π取3.14)
25.(15分)为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)(5分)求每套队服和每个足球的价格是多少?
(2)(5分)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)(5分)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
答案部分
1.D
2.C
3.D
4.D
5.C
6.A
7.C
8.D
9.C
10.C
11.8a-4b
12.100a +60b
13.0.99a
14.1.08a
15.10%x﹣y=2y﹣3
16.或
17.(a+1.25b)
18.2ab+2ac+2bc
19.
20.6a
21.解:这块空地的绿化面积为: ,
答:这块空地的绿化面积是
22.解:已知每个冰糕0.5元,小丁花了m元,则小丁吃的个数为: ;小亮花了n元,小亮吃的个数为:
23.解:∵从A地运往甲地x台,A地有机器17台,
∴从A地运往乙地(17﹣x)台,
∵甲地需要18台,
∴从B地运往甲地(18﹣x)台,
∵乙地需要14台,
∴B往乙地运14﹣(17﹣x)=x﹣3,
∴总费用=600x+500×(17﹣x)+400×(18﹣x)+800×(x﹣3)=500x+13300.(3≤x≤17,且x为整数).
24.解:阴影部分的周长:
2×3.14×5÷2+2×3.14×3÷2+(5×2-3×2)
=15.7+9.42+4
=29.12;
阴影部分的面积:
3.14×52÷2-3.14×32÷2
=39.25-14.13
=25.12;
答:阴影部分的周长C阴影是29.12,面积S阴影是25.12.
25.(1)解:设每个足球的定价是x元,则每套队服是(x+50)元,根据题意得
2(x+50)=3x,
解得x=100,
x+50=150.
答:每套队服150元,每个足球100元。
(2)解:到甲商场购买所花的费用为:150×100+100(a﹣ )=100a+14000(元),
到乙商场购买所花的费用为:150×100+0.8×100 a=80a+15000(元)
(3)解:当在两家商场购买一样合算时,100a+14000=80a+15000,解得a=50.
所以购买的足球数等于50个时,则在两家商场购买一样合算;
购买的足球数多于50个时,则到乙商场购买合算;
购买的足球数少于50个时,则到甲商场购买合算
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
