勾股定理复习(期中)[下学期]
文档属性
| 名称 | 勾股定理复习(期中)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 72.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-04-21 19:48:00 | ||
图片预览




文档简介
课件18张PPT。勾股定理复习知识回顾勾股定理:
直角三角形的两直角边为a ,b , 斜边为 c ,则有a2+ b2=c2逆定理:三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/133.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
7或25
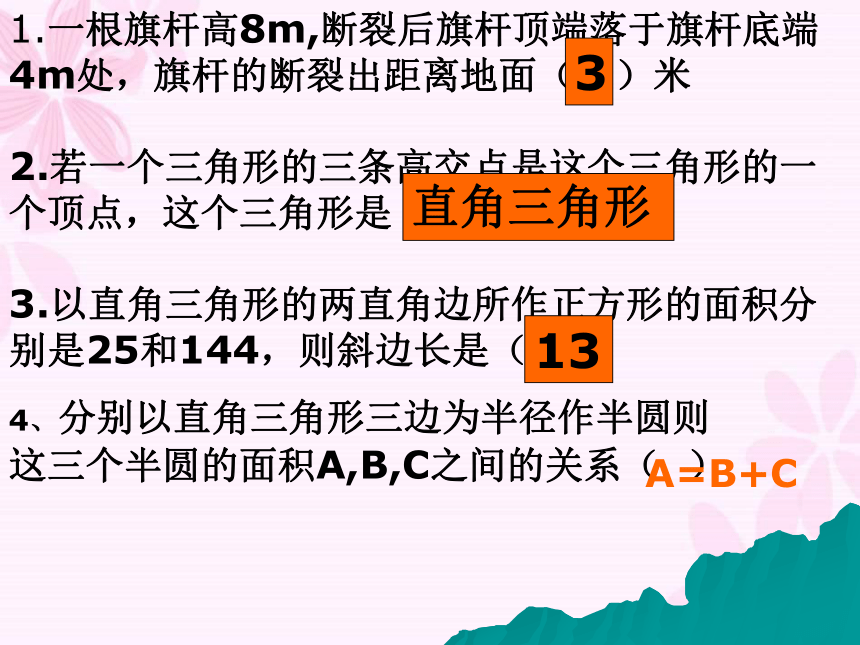
1.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂出距离地面( )米
2.若一个三角形的三条高交点是这个三角形的一个顶点,这个三角形是
3.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )3直角三角形134、分别以直角三角形三边为半径作半圆则
这三个半圆的面积A,B,C之间的关系( )
A=B+C
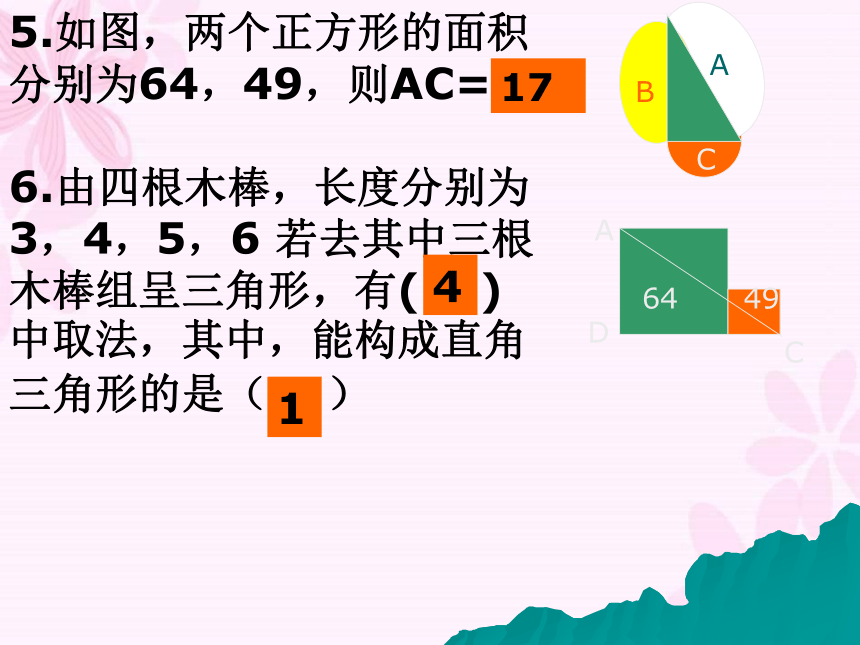
5.如图,两个正方形的面积
分别为64,49,则AC=( )
6.由四根木棒,长度分别为
3,4,5,6 若去其中三根
木棒组呈三角形,有( )
中取法,其中,能构成直角
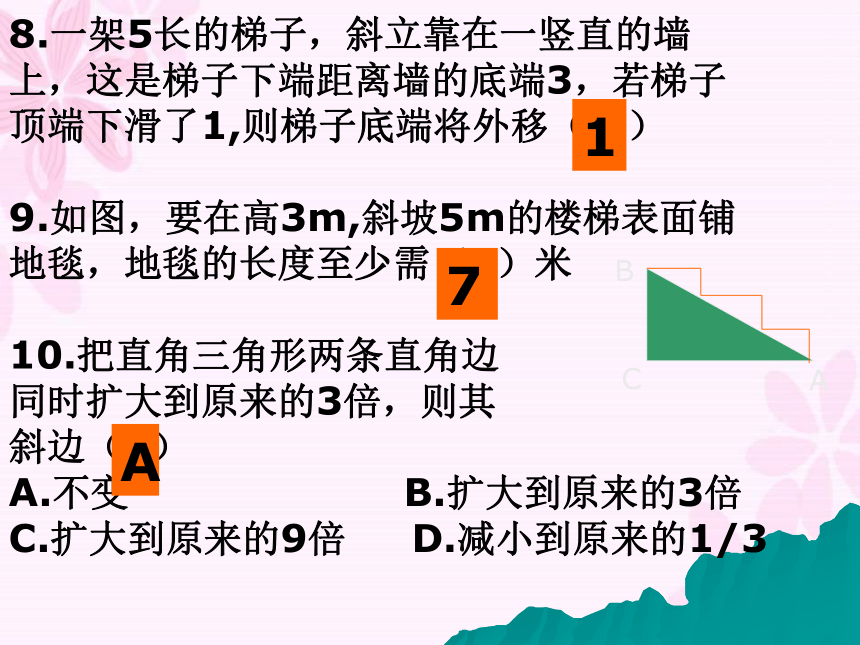
三角形的是( )11748.一架5长的梯子,斜立靠在一竖直的墙
上,这是梯子下端距离墙的底端3,若梯子
顶端下滑了1,则梯子底端将外移( )
9.如图,要在高3m,斜坡5m的楼梯表面铺
地毯,地毯的长度至少需( )米
10.把直角三角形两条直角边
同时扩大到原来的3倍,则其
斜边( )
A.不变 B.扩大到原来的3倍
C.扩大到原来的9倍 D.减小到原来的1/317A10.某直角三角形的勾与股分别是另一直角三角形勾与股的n倍,则这个三角形与另一直角三角形的弦之比是( )
A. n:1 B.1:n C.1:n2 D.n2:1
11.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 2m; B. 2.5m; C. 2.25m; D. 3m. AA13.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________________________米。 1514.已知一直角三角形的三边长都是正整
数,其中斜边长13,并且周长为30,
求其面积。
?
?
??15.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短程( 取3)是( ) A.20cm;B.10cm;C.14cm;
D.无法确定. AB60102.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm1. 观察下列几组数据:(1) 8, 15, 17; (2) 7, 12, 15; (3)12, 15, 20; (4) 7, 24, 25. 其中能作为直角三角形三边长的有( )组
A. 1 B. 2 C. 3 D. 4DB练习3. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )DB5、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——6、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————25247、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,
求AC的长。求:S四边形ABCD 8、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD例1:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。例2:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积ABCDADCDCAD1E
直角三角形的两直角边为a ,b , 斜边为 c ,则有a2+ b2=c2逆定理:三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形; 较大边c 所对的角是直角.(一)、填空题1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC=________。 2、直角三角形两直角边长分别为5和12,则它
斜边上的高为__________。 1320112460/133.已知一个Rt△的两边长分别为3和4,则第三
边长的平方是( )
7或25
1.一根旗杆高8m,断裂后旗杆顶端落于旗杆底端4m处,旗杆的断裂出距离地面( )米
2.若一个三角形的三条高交点是这个三角形的一个顶点,这个三角形是
3.以直角三角形的两直角边所作正方形的面积分别是25和144,则斜边长是( )3直角三角形134、分别以直角三角形三边为半径作半圆则
这三个半圆的面积A,B,C之间的关系( )
A=B+C
5.如图,两个正方形的面积
分别为64,49,则AC=( )
6.由四根木棒,长度分别为
3,4,5,6 若去其中三根
木棒组呈三角形,有( )
中取法,其中,能构成直角
三角形的是( )11748.一架5长的梯子,斜立靠在一竖直的墙
上,这是梯子下端距离墙的底端3,若梯子
顶端下滑了1,则梯子底端将外移( )
9.如图,要在高3m,斜坡5m的楼梯表面铺
地毯,地毯的长度至少需( )米
10.把直角三角形两条直角边
同时扩大到原来的3倍,则其
斜边( )
A.不变 B.扩大到原来的3倍
C.扩大到原来的9倍 D.减小到原来的1/317A10.某直角三角形的勾与股分别是另一直角三角形勾与股的n倍,则这个三角形与另一直角三角形的弦之比是( )
A. n:1 B.1:n C.1:n2 D.n2:1
11.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A. 2m; B. 2.5m; C. 2.25m; D. 3m. AA13.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A处。另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高_________________________米。 1514.已知一直角三角形的三边长都是正整
数,其中斜边长13,并且周长为30,
求其面积。
?
?
??15.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短程( 取3)是( ) A.20cm;B.10cm;C.14cm;
D.无法确定. AB60102.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm1. 观察下列几组数据:(1) 8, 15, 17; (2) 7, 12, 15; (3)12, 15, 20; (4) 7, 24, 25. 其中能作为直角三角形三边长的有( )组
A. 1 B. 2 C. 3 D. 4DB练习3. 直角三角形的两条直角边长为a,b,斜边上的高为h,则下列各式中总能成立的是 ( )DB5、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——6、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————25247、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,
求AC的长。求:S四边形ABCD 8、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD例1:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。例2:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积ABCDADCDCAD1E
