勾股定理的逆定理(一)[下学期]
文档属性
| 名称 | 勾股定理的逆定理(一)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-27 00:00:00 | ||
图片预览





文档简介
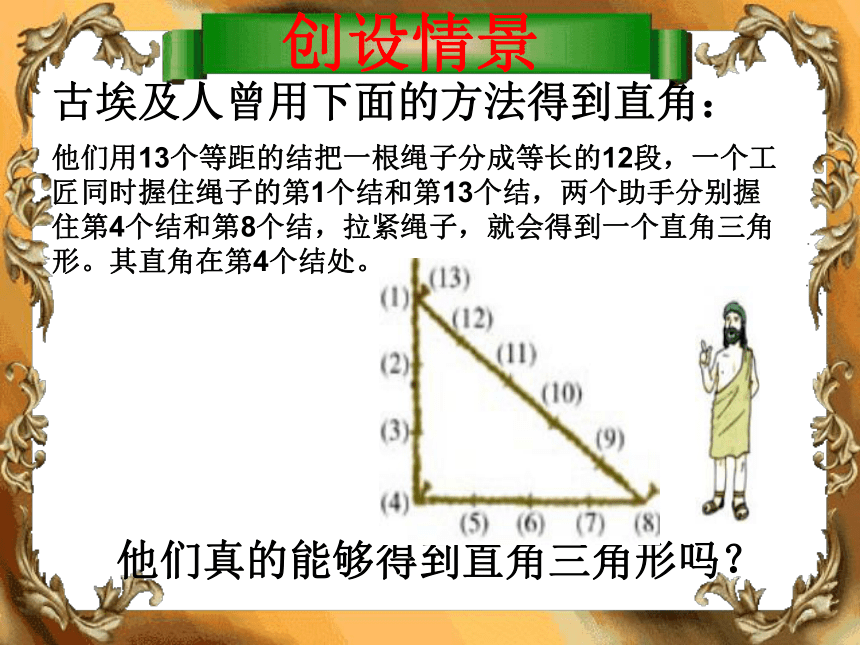
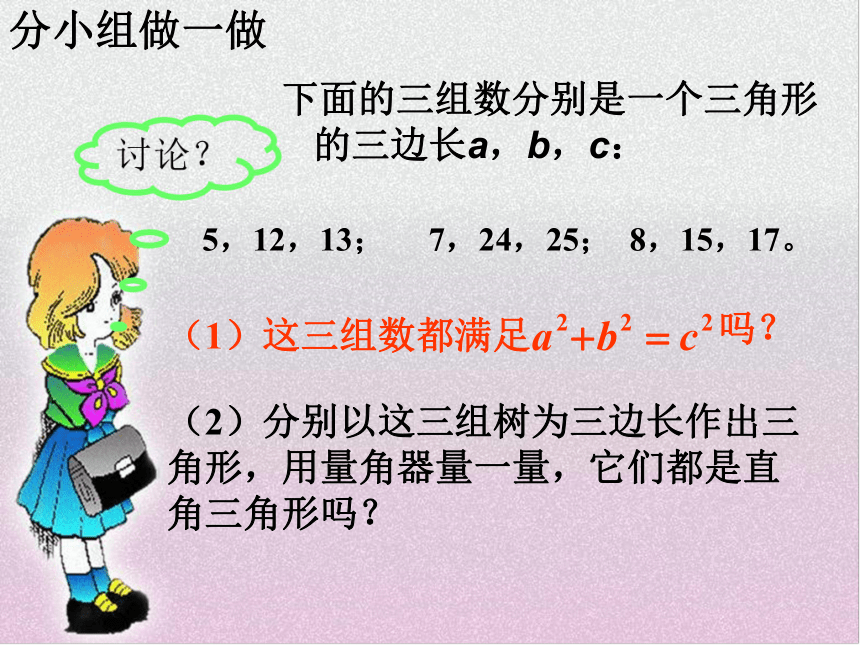
课件15张PPT。18.2勾股定理的逆定理你能用什么方法来证明一个三角形是直角三角形⑴有一个角是直角的三角形是直角三角形⑵有两条边互相垂直的三角形是直角三角形知识回顾他们真的能够得到直角三角形吗?创设情景他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。古埃及人曾用下面的方法得到直角:下面的三组数分别是一个三角形的三边长a,b,c:5,12,13; 7,24,25; 8,15,17。(2)分别以这三组树为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?分小组做一做 如果三角形的三边长a,b,c有关系(1)上述结论中,哪条边所对的角是直角?勾股定理的逆定理那么这个三角形是直角三角形.(2)如果三角形中较短两边的平方和不等于
最长的平方,那么这个三角形是直角三角形吗?证明: 则有例1 判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17
(2) a=13, b=14,c=15解:(1)能够成为直角三角形三边长的三个正整数,称为勾股数(或勾股弦数)。你能举几组勾股数吗?有什么规律?1.已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是____度;2.△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为____;90°1803.三角形的三边长为 8 ,15 ,17 ,那么最短边上的高为____;154.若△ABC中 ,AB=5 ,BC=12 ,
AC=13 ,则AC边上的高长为__5.三角形的三边长a,b,c满足 (a+b)2=c2+2ab ,则这个三角形是( )
A 等边三角形 B钝角三角形
C 直角三角形 D 锐角三角形C5.在Rt△ABC中,斜边AB=1 ,
则 AB2 + BC2 + CA2 =____;26.等腰三角形ABC中,若 AB =AC =10 ,BC =6 ,
则△ABC的面积为____;8.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个
C 3个 D 4个BA 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形3.工人师傅想要检测一扇小门两边 AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗?小结⑴勾股定理的逆定理⑵勾股定理的逆定理的应用这节课还有什么收获,说出来与大家分享
最长的平方,那么这个三角形是直角三角形吗?证明: 则有例1 判断由线段a、 b 、 c 组成的三角形是不是直角三角形:
(1)a=15, b=8, c=17
(2) a=13, b=14,c=15解:(1)能够成为直角三角形三边长的三个正整数,称为勾股数(或勾股弦数)。你能举几组勾股数吗?有什么规律?1.已知三角形的三边长为 9 ,12 ,15 ,则这个三角形的最大角是____度;2.△ABC的三边长为 9 ,40 ,41 ,则△ABC的面积为____;90°1803.三角形的三边长为 8 ,15 ,17 ,那么最短边上的高为____;154.若△ABC中 ,AB=5 ,BC=12 ,
AC=13 ,则AC边上的高长为__5.三角形的三边长a,b,c满足 (a+b)2=c2+2ab ,则这个三角形是( )
A 等边三角形 B钝角三角形
C 直角三角形 D 锐角三角形C5.在Rt△ABC中,斜边AB=1 ,
则 AB2 + BC2 + CA2 =____;26.等腰三角形ABC中,若 AB =AC =10 ,BC =6 ,
则△ABC的面积为____;8.长度分别为 3 , 4 , 5 , 12 ,13 的五根木棒能搭成(首尾连接)直角三角形的个数为( )
A 1个 B 2个
C 3个 D 4个BA 例 3.在△ABC中,a=15, b=17, c=8,求此三角形的面积。∴△ABC为直角三角形,且∠B=90°
∴ △ABC的面积为已知a.b.c为△ABC的三边,且满足 a2c2 – b2c2=a4 – b4,试判断△ABC的形状.
解 ∵ a2c2- b2c2 = a4 – b4 (1)
∴ c2(a2 – b2) = (a2+ b2) (a2- b2) (2)
∴ c2 = a2 + b2 (3)
∴ △ABC是直角三角形
问: (1) 上述解题过程,从哪一步开始出现错误?请写出该步的代号___
(2) 错误原因是_________
(3) 本题正确的结论是________3a2- b2可能是0直角三角形或等腰三角形3.工人师傅想要检测一扇小门两边 AB .CD 是否垂直于底边 BC,但他只带了一把卷尺,你能替工人师傅想办法完成任务吗?小结⑴勾股定理的逆定理⑵勾股定理的逆定理的应用这节课还有什么收获,说出来与大家分享
