勾股定理的逆定理1[下学期]
文档属性
| 名称 | 勾股定理的逆定理1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 105.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-31 12:25:00 | ||
图片预览








文档简介
课件23张PPT。命题:对一件事情判断的语句,称为命题。命题的组成:由题设和结论两部分组成。常可添加“如果……那么……”来分清。例如:“对顶角相等。”
可添加为:“如果两个角是对顶角;那么这两个角相等。”
请指出下列命题的题设和结论:1、同位角相等,两直线平行;
2、两个全等三角形的对应角、对应边相等。
3、等腰三角形的两底角相等。互逆命题:
如果一个命题的条件和结论分别是另一个命题的结论和条件。我们把这样的两个命题称为互逆命题。如果把其中的一个命题称为原命题,那么另一个命题就叫做它的逆命题。你知道原命题与它的逆命题的关系吗?你会说出原命题的逆命题吗?对顶角相等同旁内角互补,两直线平行全等三角形的对应边相等两个实数相等,这两个实数的平方也相等定理:用推理的方法判断为正确的命题。注意:任何一个命题都有逆命题,但任何一个定理不一定有逆定理。勾股定理:如果直角三角形的两条直角
边长分别为a,b,斜边为c,那么勾股定理逆定理古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。他们真的能够得到直角三角形吗?做一做下面的三组数分别是一个三角形的三边长a,b,c:5,12,13; 7,24,25; 8,15,17。勾股定理的逆命题 如果三角形的一条边的平方等于其它两条边的平方和,那么这个三角形是直角三角形。
已知:
求证:
证明:勾股定理的逆定理如果三角形的一条边的平方等于其它两条边的平方和,那么这个三角形是直角三角形。
几何语言叙述:勾股数 119 169
3367 4852
4601 6649
13500 12709 18541
360 319 481
960 799 1249
2400 1679 29292700 1771 3229
90 56 106
4961 8161
65 97
45 75
481 769
240 161 289毕发现勾股数
2n+1 2n2+2n 2n2+2n+1柏拉图发现勾股数
2m m2-1 m2+1九章算术中记载
m2-n2 2mn m2+n2练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 (3) a=41 b=9 c=40 (4) a:b: c=3:4:5 (2) a=1 b=2 c= (5) a2=b2-c2 这是剪纸后的余料,你能判定剪下的两个三角形是直角三角形吗?12159153639已知:在△ ABC中, AB=15cm,AC=20cm, BC=25cm,AD是BC边上的高线。
求:AD的长。ABCD在ΔABC中,AB=13cm,BC=10cm,BC上的中线AD=12cm,求证:ΔABC是等腰三角形ABCD
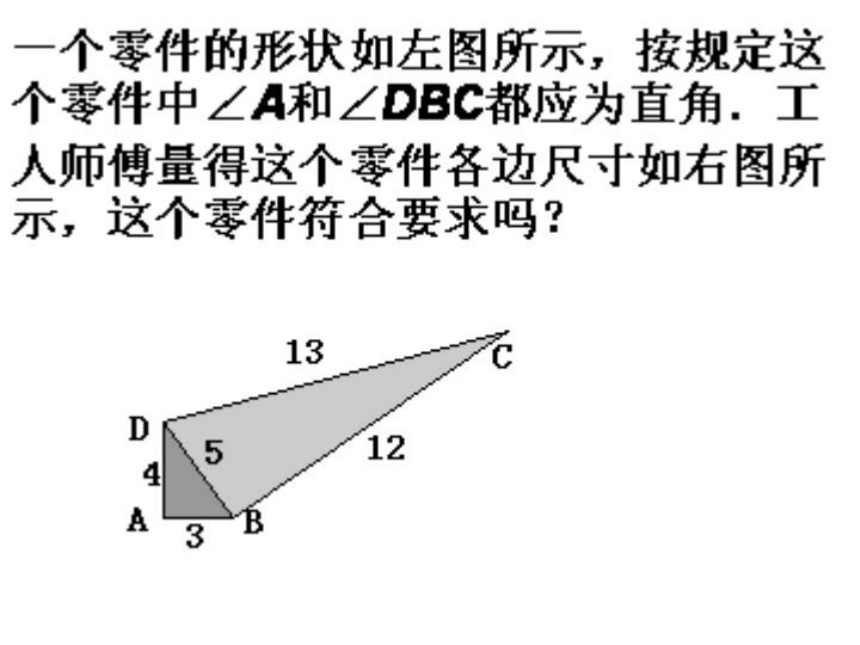
已知:如图,四边形ABCD中,
∠B= AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
ABCD
已知:如图,四边形ABCD中,
∠B= AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
ABCD求(1) S四边形ABCD。(2)∠ DCA的度数CD=cm, AD=2cm,AC⊥AB。已知:在四边形ABCD中,AB=3cm, BC=5cm,例2如果一个三角形的三边长分别为
则这三角形是直角三角形
如果是直角三角形,你能判断出a,b,c中谁是斜边吗?1.本节课我学到了什么?
2.本节课的知识与前面学过的什么知识有联系?
3.联系实际:学知识后,对你在哪些方面有帮助?
4.本节课我感到有点困惑是什么?
可添加为:“如果两个角是对顶角;那么这两个角相等。”
请指出下列命题的题设和结论:1、同位角相等,两直线平行;
2、两个全等三角形的对应角、对应边相等。
3、等腰三角形的两底角相等。互逆命题:
如果一个命题的条件和结论分别是另一个命题的结论和条件。我们把这样的两个命题称为互逆命题。如果把其中的一个命题称为原命题,那么另一个命题就叫做它的逆命题。你知道原命题与它的逆命题的关系吗?你会说出原命题的逆命题吗?对顶角相等同旁内角互补,两直线平行全等三角形的对应边相等两个实数相等,这两个实数的平方也相等定理:用推理的方法判断为正确的命题。注意:任何一个命题都有逆命题,但任何一个定理不一定有逆定理。勾股定理:如果直角三角形的两条直角
边长分别为a,b,斜边为c,那么勾股定理逆定理古埃及人曾用下面的方法得到直角:
他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。他们真的能够得到直角三角形吗?做一做下面的三组数分别是一个三角形的三边长a,b,c:5,12,13; 7,24,25; 8,15,17。勾股定理的逆命题 如果三角形的一条边的平方等于其它两条边的平方和,那么这个三角形是直角三角形。
已知:
求证:
证明:勾股定理的逆定理如果三角形的一条边的平方等于其它两条边的平方和,那么这个三角形是直角三角形。
几何语言叙述:勾股数 119 169
3367 4852
4601 6649
13500 12709 18541
360 319 481
960 799 1249
2400 1679 29292700 1771 3229
90 56 106
4961 8161
65 97
45 75
481 769
240 161 289毕发现勾股数
2n+1 2n2+2n 2n2+2n+1柏拉图发现勾股数
2m m2-1 m2+1九章算术中记载
m2-n2 2mn m2+n2练习一下面以a,b,c为边长的三角形是不是直角三角形?如果是那么哪一个角是直角?(1) a=25 b=20 c=15 (3) a=41 b=9 c=40 (4) a:b: c=3:4:5 (2) a=1 b=2 c= (5) a2=b2-c2 这是剪纸后的余料,你能判定剪下的两个三角形是直角三角形吗?12159153639已知:在△ ABC中, AB=15cm,AC=20cm, BC=25cm,AD是BC边上的高线。
求:AD的长。ABCD在ΔABC中,AB=13cm,BC=10cm,BC上的中线AD=12cm,求证:ΔABC是等腰三角形ABCD
已知:如图,四边形ABCD中,
∠B= AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
ABCD
已知:如图,四边形ABCD中,
∠B= AB=3,BC=4,CD=12,AD=13求四边形ABCD的面积
ABCD求(1) S四边形ABCD。(2)∠ DCA的度数CD=cm, AD=2cm,AC⊥AB。已知:在四边形ABCD中,AB=3cm, BC=5cm,例2如果一个三角形的三边长分别为
则这三角形是直角三角形
如果是直角三角形,你能判断出a,b,c中谁是斜边吗?1.本节课我学到了什么?
2.本节课的知识与前面学过的什么知识有联系?
3.联系实际:学知识后,对你在哪些方面有帮助?
4.本节课我感到有点困惑是什么?
