北师大版数学八年级下册 2.5一元一次不等式与一次函数 课件(共13张PPT)
文档属性
| 名称 | 北师大版数学八年级下册 2.5一元一次不等式与一次函数 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 406.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 10:55:22 | ||
图片预览

文档简介
(共13张PPT)
一元一次不等式与一次函数
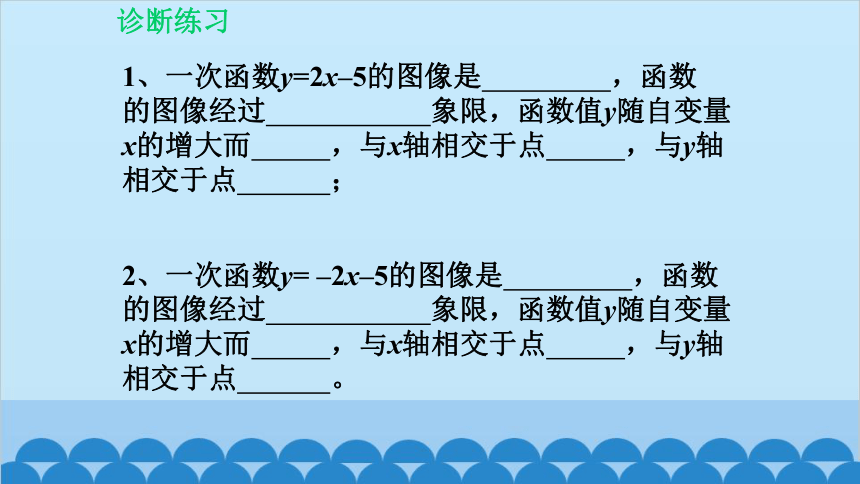
1、一次函数y=2x–5的图像是 ,函数
的图像经过 象限,函数值y随自变量
x的增大而 ,与x轴相交于点 ,与y轴
相交于点 ;
诊断练习
2、一次函数y= –2x–5的图像是 ,函数
的图像经过 象限,函数值y随自变量
x的增大而 ,与x轴相交于点 ,与y轴
相交于点 。
情景引入
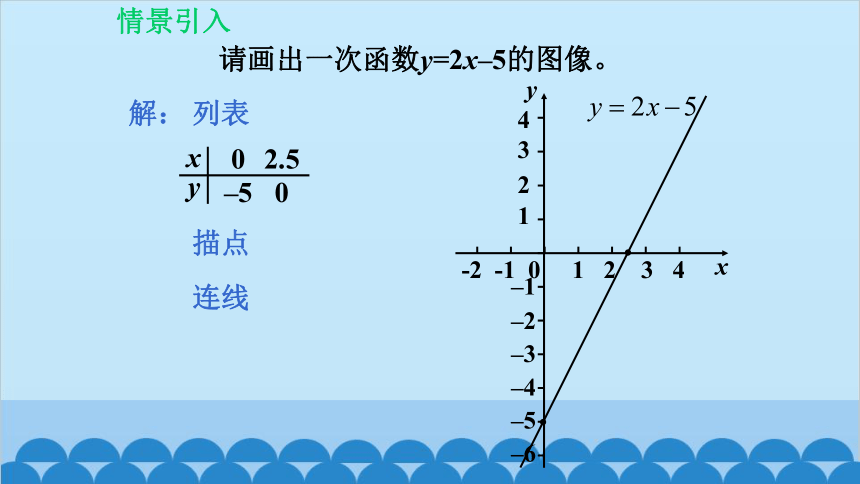
请画出一次函数y=2x–5的图像。
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
解:
列表
x
y
0
–5
2.5
0
描点
连线
新知探究
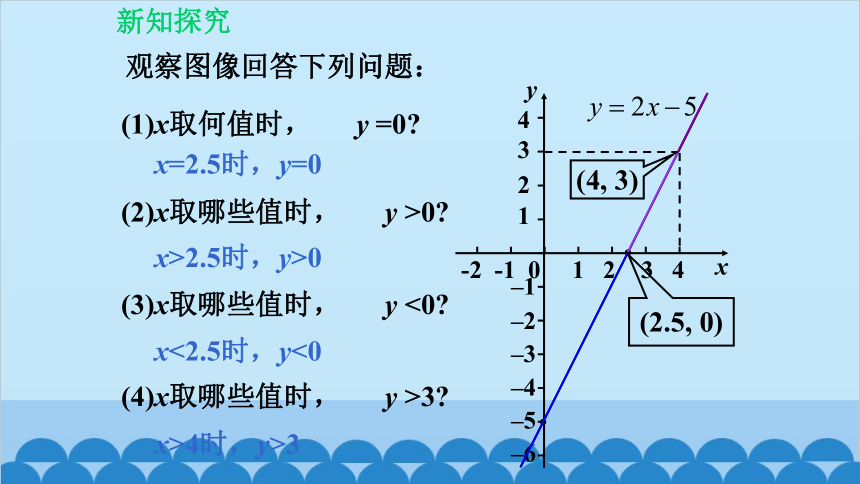
观察图像回答下列问题:
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
(1)x取何值时, y =0
(2)x取哪些值时, y >0
x=2.5时,y=0
(2.5, 0)
x>2.5时,y>0
(3)x取哪些值时, y <0
(4)x取哪些值时, y >3
x<2.5时,y<0
x>4时,y>3
(4, 3)
新知探究
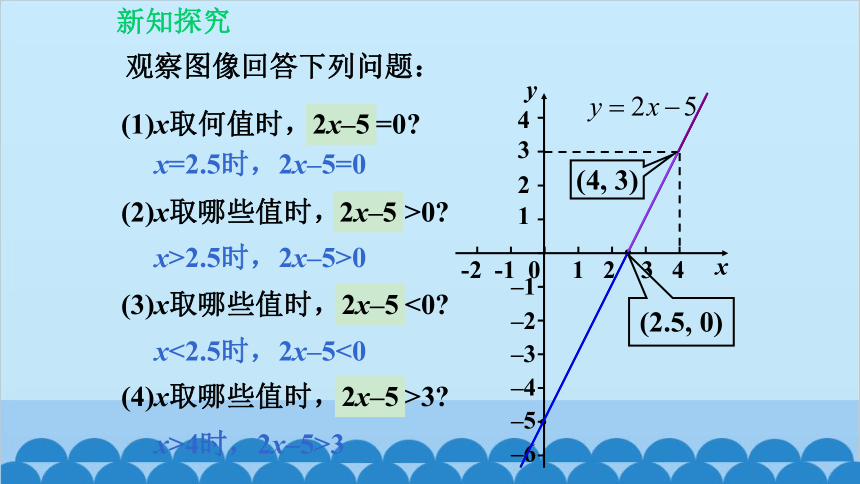
观察图像回答下列问题:
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
(1)x取何值时, y =0
(2)x取哪些值时, y >0
x=2.5时,2x–5=0
(2.5, 0)
x>2.5时,2x–5>0
(3)x取哪些值时, y <0
(4)x取哪些值时, y >3
x<2.5时,2x–5<0
x>4时,2x–5>3
(4, 3)
2x–5
2x–5
2x–5
2x–5
新知归纳
转化思想:
一次函数问题
一次不等式(方程)
问题
转化
合作交流
ⅰ、如果 y= –2x–5 , 那么当x取何值时 , y>0
y
-5 -4 -3 -2 -1 0 1
x
3
2
1
–1
–2
–3
–4
–5
–6
解法一:
由图像可知:
当x<–2.5时,y>0
解法二:
解不等式–2x–5>0,得
x<–2.5
新知归纳
求函数问题的方法:
(1)图像法:
画出函数图像解决函数问题;
(2)列式法:
列不等式(方程)求解集解决函数问题。
ⅱ、已知y1= –x+3,y2= 3x – 4,当x取何值时:
(1) y1>y2 ? (2) y1合作交流
范例讲解
例1、兄弟俩赛跑,哥哥先让弟弟跑9m,然后自
己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4
m。列出函数关系式,作出函数图像,观察图像
回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过
100m?
1、如图,l1反映了某产品的销售收入与销售量之
间的关系,l2反映了该产品的销售成本与销售量
之间的关系,当销售收入大于销售成本时,该产
品开始盈利。该产品的销售量达到多少吨时,生
产该产品才能盈利?
巩固练习
2、甲、乙两辆摩托车从相距20km的A、B两地相
向而行,图中l1、 l2分别表示甲、乙两辆摩托车离
A地的距离s(km)与行驶时间t(h)之间的函数关系。
(1)哪辆摩托车的速度快?
(2)经过多长时间,甲车
行驶到A、B两地的中点?
巩固练习
课堂小结
1、转化思想:
一次函数问题
一次不等式问题
转化
2、求函数问题的方法:
(1)图像法:
画出函数图像解决函数问题;
(2)列式法:
列不等式求解集解决函数问题。
一元一次不等式与一次函数
1、一次函数y=2x–5的图像是 ,函数
的图像经过 象限,函数值y随自变量
x的增大而 ,与x轴相交于点 ,与y轴
相交于点 ;
诊断练习
2、一次函数y= –2x–5的图像是 ,函数
的图像经过 象限,函数值y随自变量
x的增大而 ,与x轴相交于点 ,与y轴
相交于点 。
情景引入
请画出一次函数y=2x–5的图像。
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
解:
列表
x
y
0
–5
2.5
0
描点
连线
新知探究
观察图像回答下列问题:
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
(1)x取何值时, y =0
(2)x取哪些值时, y >0
x=2.5时,y=0
(2.5, 0)
x>2.5时,y>0
(3)x取哪些值时, y <0
(4)x取哪些值时, y >3
x<2.5时,y<0
x>4时,y>3
(4, 3)
新知探究
观察图像回答下列问题:
y
-2 -1 0 1 2 3 4
x
4
3
2
1
–1
–2
–3
–4
–5
–6
(1)x取何值时, y =0
(2)x取哪些值时, y >0
x=2.5时,2x–5=0
(2.5, 0)
x>2.5时,2x–5>0
(3)x取哪些值时, y <0
(4)x取哪些值时, y >3
x<2.5时,2x–5<0
x>4时,2x–5>3
(4, 3)
2x–5
2x–5
2x–5
2x–5
新知归纳
转化思想:
一次函数问题
一次不等式(方程)
问题
转化
合作交流
ⅰ、如果 y= –2x–5 , 那么当x取何值时 , y>0
y
-5 -4 -3 -2 -1 0 1
x
3
2
1
–1
–2
–3
–4
–5
–6
解法一:
由图像可知:
当x<–2.5时,y>0
解法二:
解不等式–2x–5>0,得
x<–2.5
新知归纳
求函数问题的方法:
(1)图像法:
画出函数图像解决函数问题;
(2)列式法:
列不等式(方程)求解集解决函数问题。
ⅱ、已知y1= –x+3,y2= 3x – 4,当x取何值时:
(1) y1>y2 ? (2) y1
范例讲解
例1、兄弟俩赛跑,哥哥先让弟弟跑9m,然后自
己才开始跑。已知弟弟每秒跑3m,哥哥每秒跑4
m。列出函数关系式,作出函数图像,观察图像
回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20m?谁先跑过
100m?
1、如图,l1反映了某产品的销售收入与销售量之
间的关系,l2反映了该产品的销售成本与销售量
之间的关系,当销售收入大于销售成本时,该产
品开始盈利。该产品的销售量达到多少吨时,生
产该产品才能盈利?
巩固练习
2、甲、乙两辆摩托车从相距20km的A、B两地相
向而行,图中l1、 l2分别表示甲、乙两辆摩托车离
A地的距离s(km)与行驶时间t(h)之间的函数关系。
(1)哪辆摩托车的速度快?
(2)经过多长时间,甲车
行驶到A、B两地的中点?
巩固练习
课堂小结
1、转化思想:
一次函数问题
一次不等式问题
转化
2、求函数问题的方法:
(1)图像法:
画出函数图像解决函数问题;
(2)列式法:
列不等式求解集解决函数问题。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
