勾股定理[下学期]
图片预览


文档简介
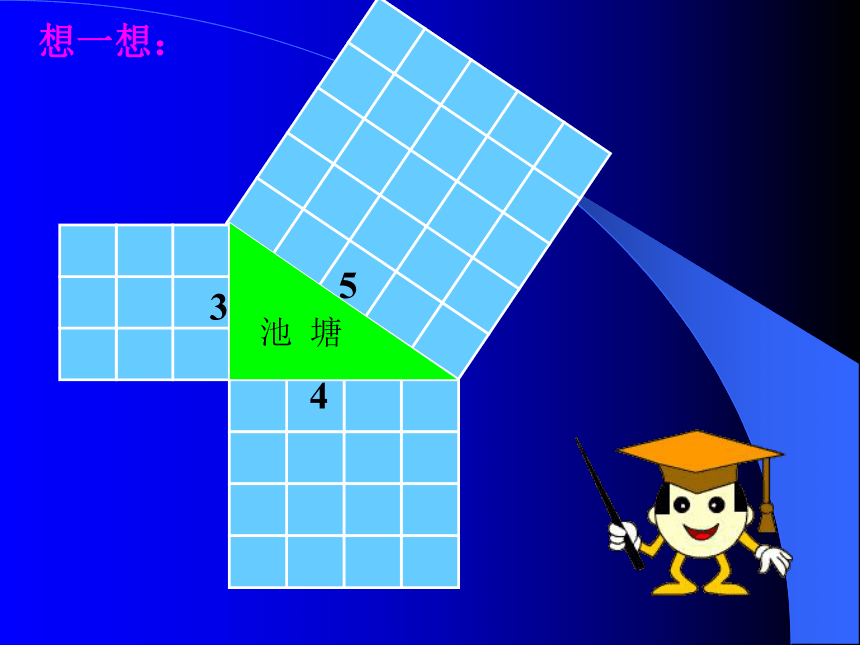
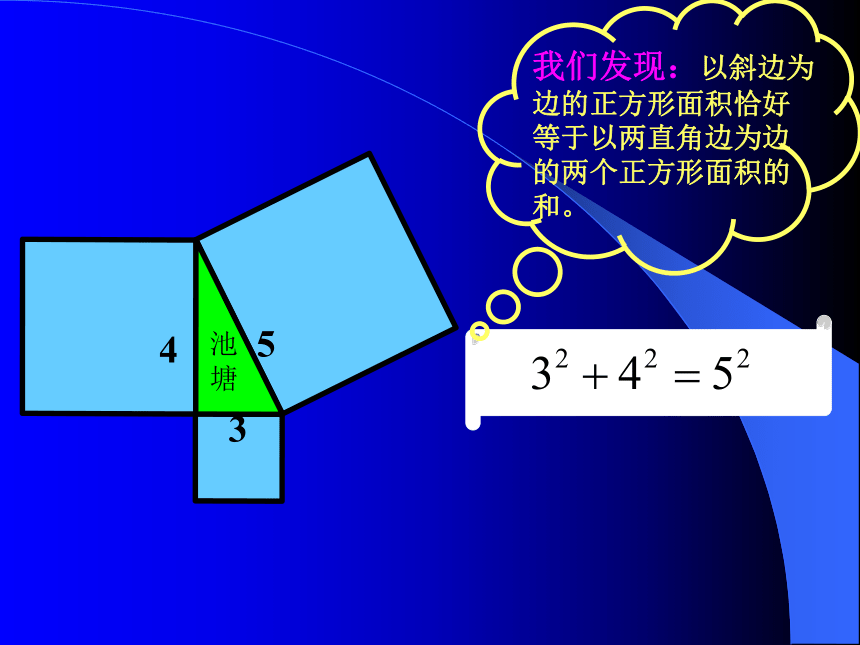
课件12张PPT。勾股定理想一想:我们发现:以斜边为边的正方形面积恰好等于以两直角边为边的两个正方形面积的和。
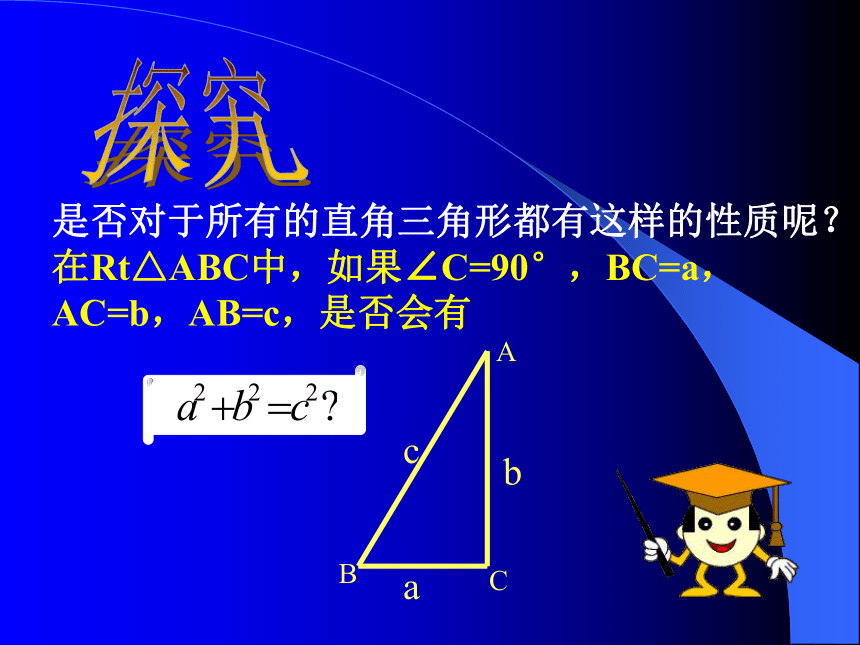
探究证明aaabbbccc
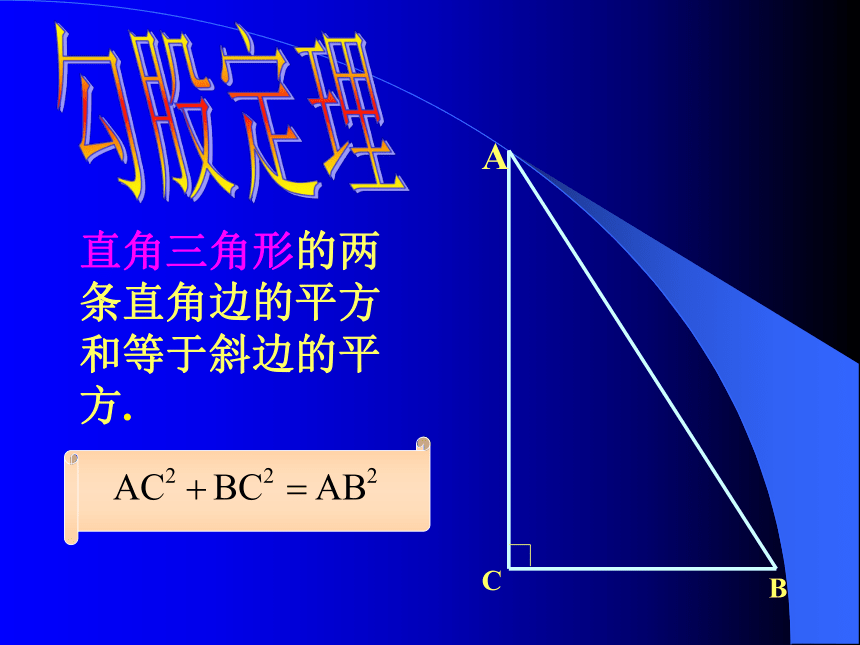
直角三角形的两条直角边的平方和等于斜边的平方.勾股定理什么是“勾、股”呢?
在中国古代,人们把弯曲成直角的
手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.有一个十分重要而著名的定理,它不仅在数学中有着广泛的应用,而且在其它自然学科中也常常用到,这就是勾股定理.商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。
这就是著名的勾股定理.勾股定理在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯现在你对勾股定理有了哪些了解呢?说一说:作业:
1、P103.B2
再见
探究证明aaabbbccc
直角三角形的两条直角边的平方和等于斜边的平方.勾股定理什么是“勾、股”呢?
在中国古代,人们把弯曲成直角的
手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.有一个十分重要而著名的定理,它不仅在数学中有着广泛的应用,而且在其它自然学科中也常常用到,这就是勾股定理.商高是公元前十一世纪的中国人。当时中国的朝代是西周,是奴隶社会时期。在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”商高那段话的意思就是说:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(就是弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。
这就是著名的勾股定理.勾股定理在国外,相传这个定理是公元前500多年时古希腊数学家毕达哥拉斯首先发现的。因此又称此定理为“毕达哥拉斯定理”。法国和比利时称它为“驴桥定理”,埃及称它为“埃及三角形”等。但他们发现的时间都比我国要迟得多。 毕达哥拉斯定理Pythagoras’ theorem毕达哥拉斯现在你对勾股定理有了哪些了解呢?说一说:作业:
1、P103.B2
再见
