勾股定理[下学期]
图片预览


文档简介
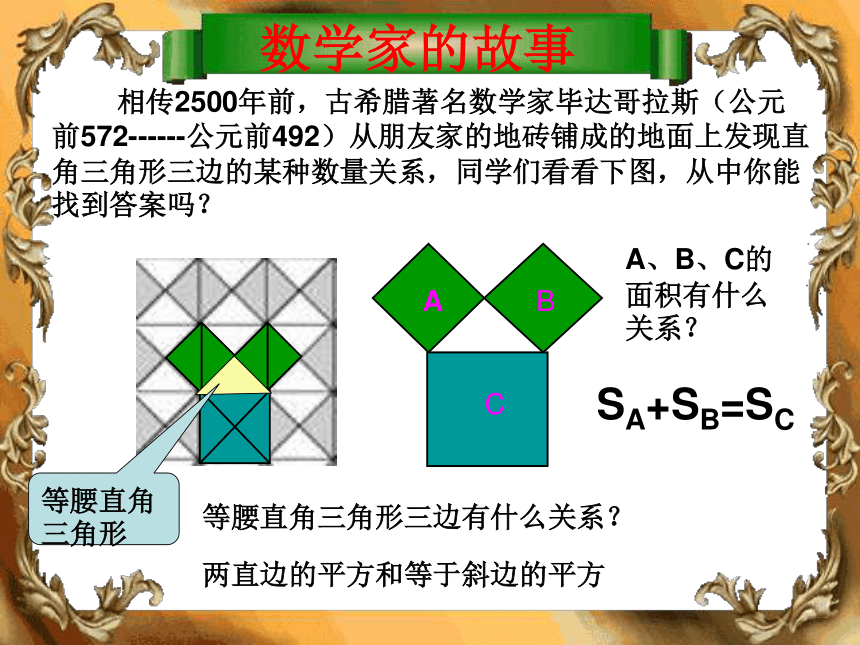
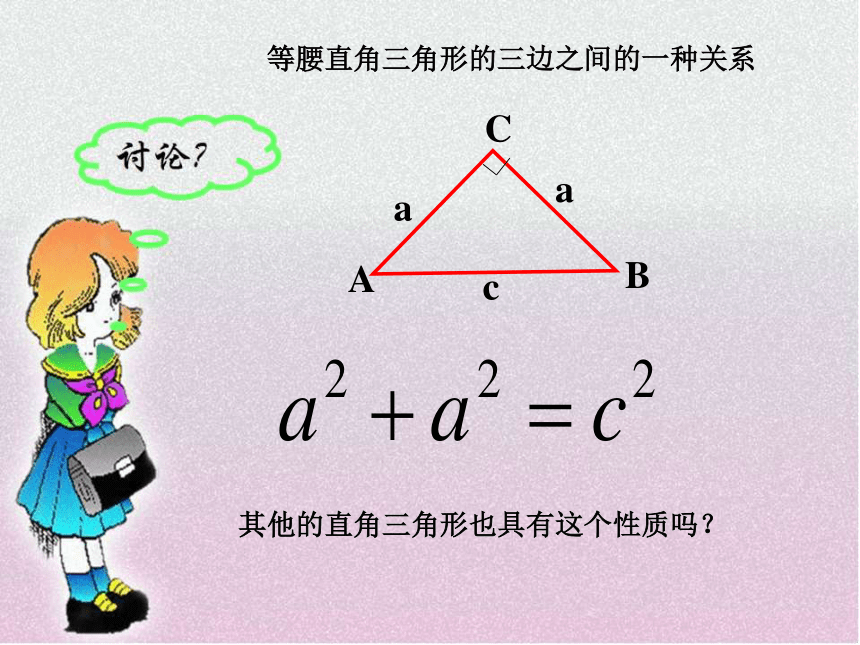
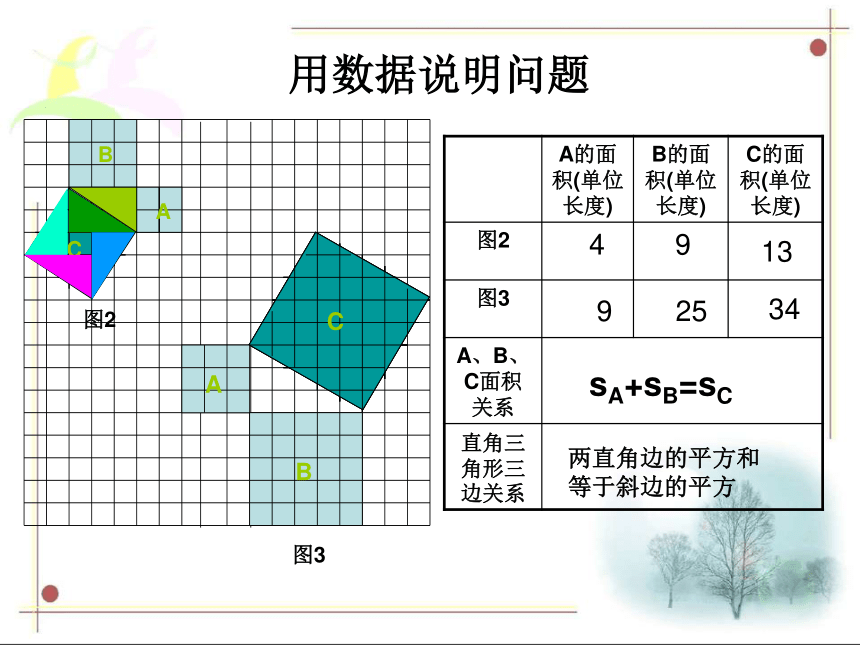
课件17张PPT。勾 股 定 理 相传2500年前,古希腊著名数学家毕达哥拉斯(公元前572------公元前492)从朋友家的地砖铺成的地面上发现直角三角形三边的某种数量关系,同学们看看下图,从中你能找到答案吗?A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方等腰直角三角形数学家的故事等腰直角三角形的三边之间的一种关系其他的直角三角形也具有这个性质吗?ABC图2图3491392534sA+sB=sC两直角边的平方和
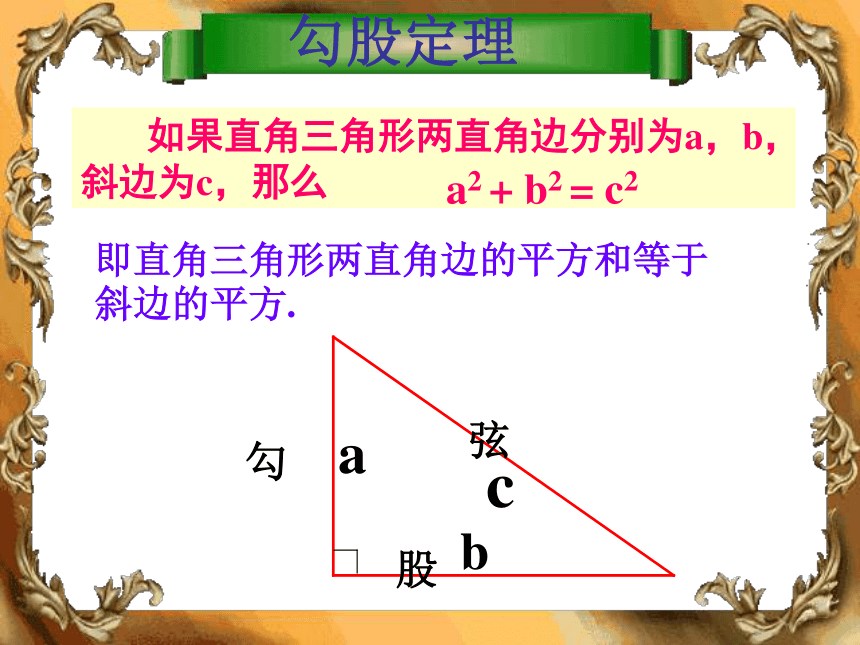
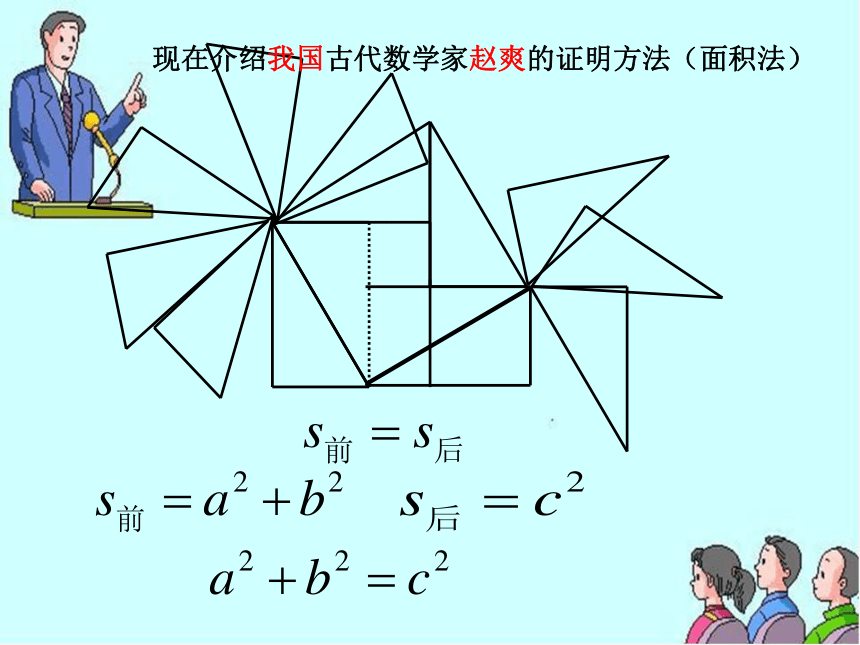
等于斜边的平方用数据说明问题 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理现在介绍我国古代数学家赵爽的证明方法(面积法)a2 + b2 = c2的几种变形和作用已知两边就可求出第三边的长度a2 + b2 = c2⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑴由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑵由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑶由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑷设由勾股定理得一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?所以木板____ 从门框内通过.大于能因为AC______木板的宽,因此,AC= >连结AC,在Rt△ABC中,根据勾股定理补充{(a>0)(a<0)一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?分析:DB=OD-OB,求BD,可以 先求OB,OD.梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中在Rt△COD中,BD=OD-OB = 2.236 -1.658 ≈0.580.58 m课堂练习课堂小结⑴勾股定理及应用。已知两边就可求出第三边的长度⑵二次根式的化简⑶对任意非负数的开平方运算
等于斜边的平方用数据说明问题 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理现在介绍我国古代数学家赵爽的证明方法(面积法)a2 + b2 = c2的几种变形和作用已知两边就可求出第三边的长度a2 + b2 = c2⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑴由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑵由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑶由勾股定理得⑴若 a=8,b=6, 求c:在Rt△ABC中, ∠C=⑵若 a=5,c=13, 求b;⑶若b=8,c=12, 求a;⑷若a:b=2:3,c=13
求a、b的长解:⑷设由勾股定理得一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?所以木板____ 从门框内通过.大于能因为AC______木板的宽,因此,AC= >连结AC,在Rt△ABC中,根据勾股定理补充{(a>0)(a<0)一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?分析:DB=OD-OB,求BD,可以 先求OB,OD.梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中在Rt△COD中,BD=OD-OB = 2.236 -1.658 ≈0.580.58 m课堂练习课堂小结⑴勾股定理及应用。已知两边就可求出第三边的长度⑵二次根式的化简⑶对任意非负数的开平方运算
