18.1 勾股定理[下学期]
文档属性
| 名称 | 18.1 勾股定理[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 869.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-24 00:00:00 | ||
图片预览





文档简介
课件40张PPT。第十八章 勾股定理的应用 毕达哥拉斯(公元前572----前492年),古希腊著名的哲学家、
数学家、天文学家。s1s2s3
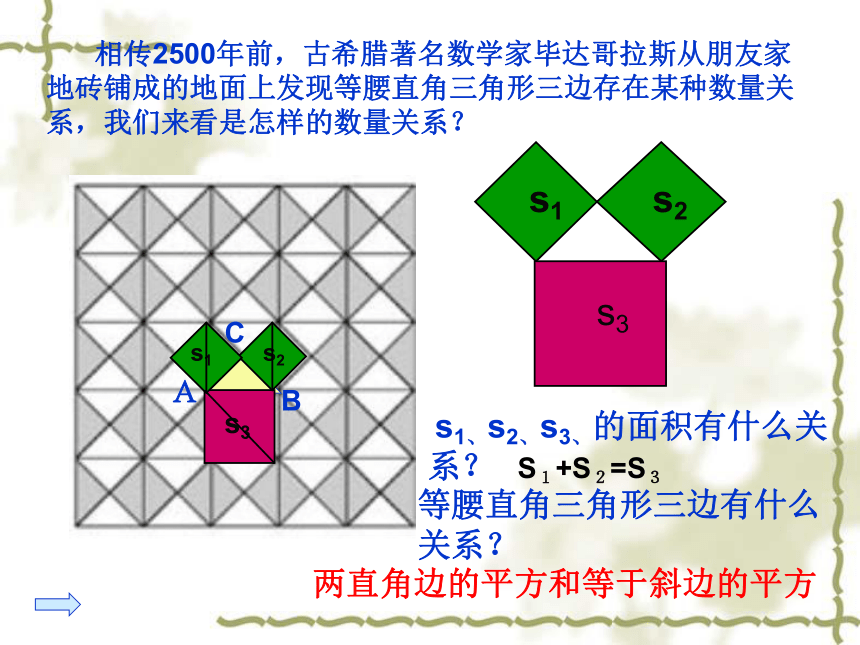
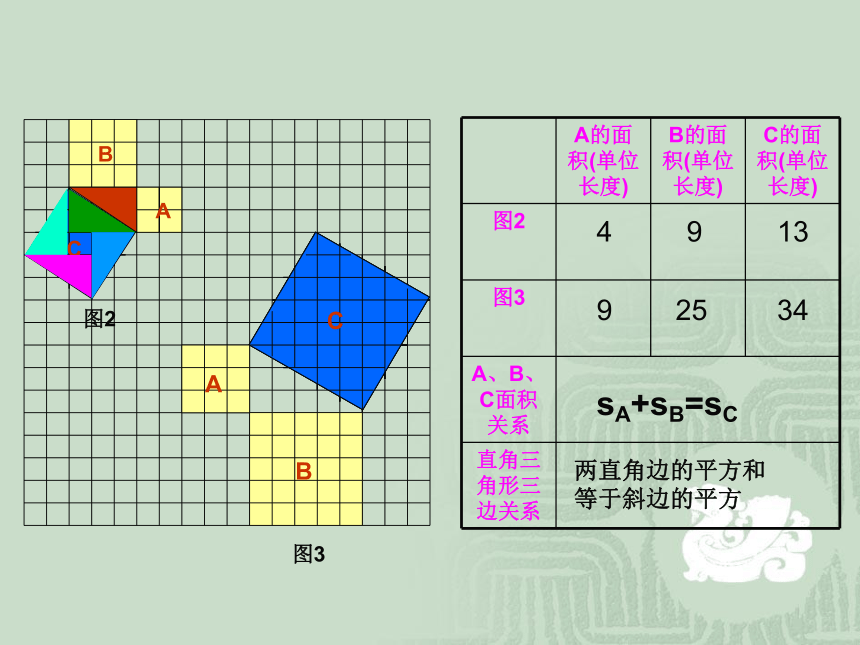
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家地砖铺成的地面上发现等腰直角三角形三边存在某种数量关系,我们来看是怎样的数量关系? s1、s2、s3、的面积有什么关系?等腰直角三角形三边有什么关系?S1+S2=S3两直角边的平方和等于斜边的平方ABC图2图3491392534sA+sB=sC两直角边的平方和
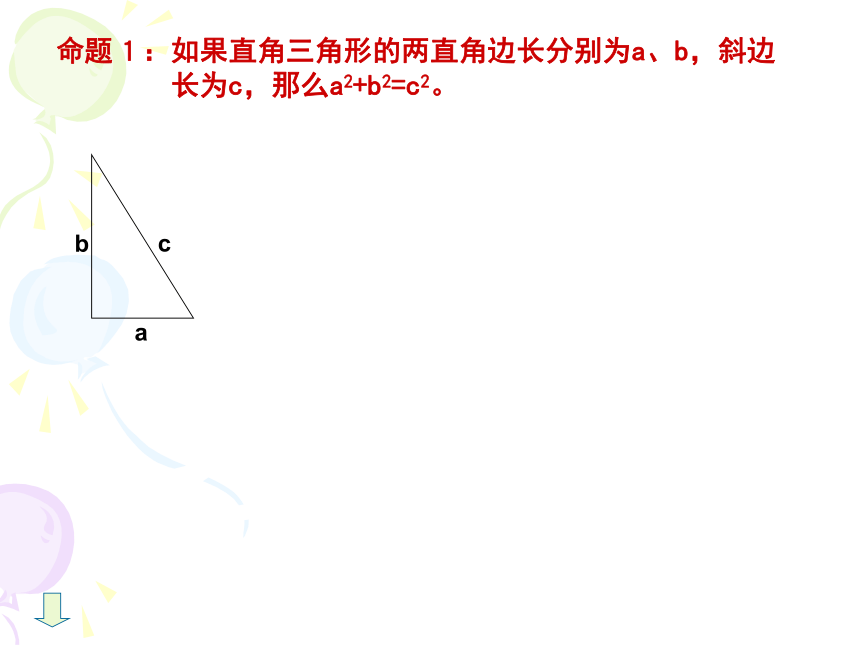
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边
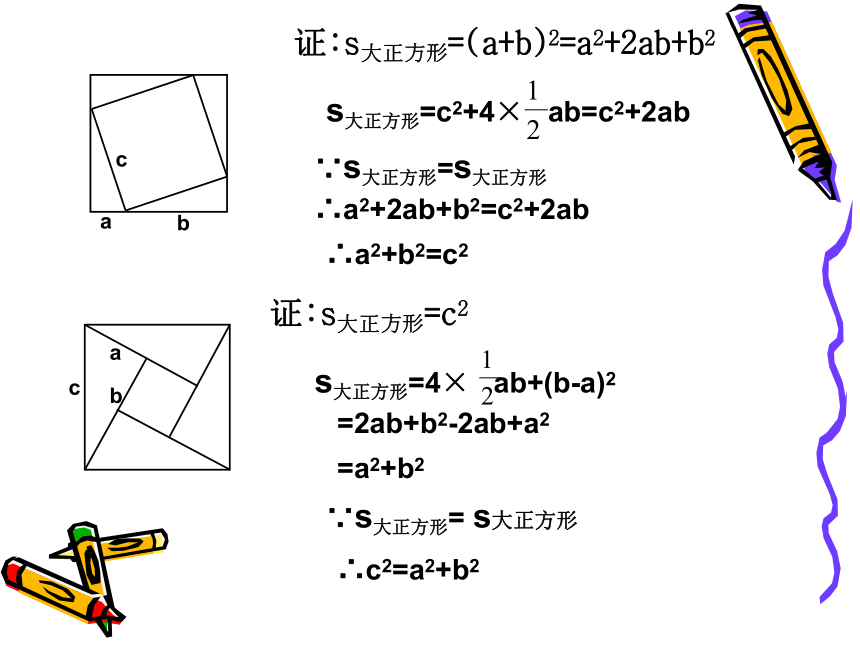
长为c,那么a2+b2=c2。abcabcabc证:s大正方形=(a+b)2=a2+2ab+b2
证:s大正方形=c2
s大正方形=c2+4× ab=c2+2ab∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∵s大正方形= s大正方形
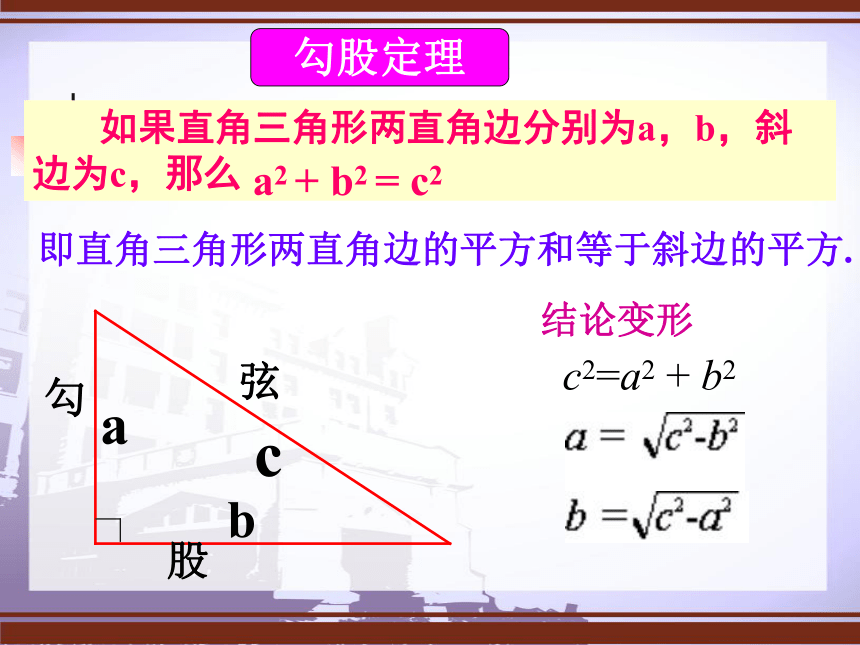
∴c2=a2+b2 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股弦结论变形
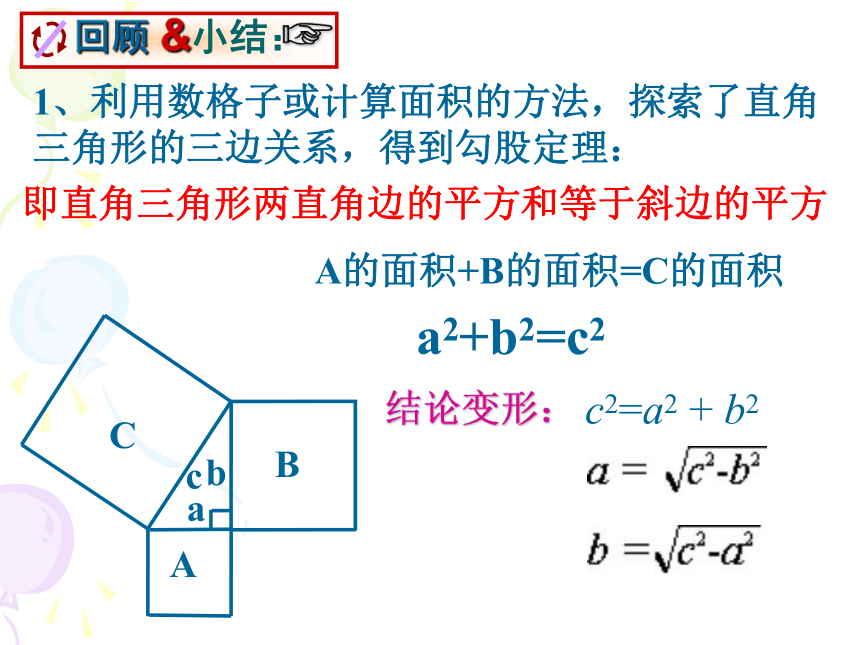
c2=a2 + b21、利用数格子或计算面积的方法,探索了直角三角形的三边关系,得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2结论变形:c2=a2 + b2常见的勾股数及特殊的三边
3、4、5;
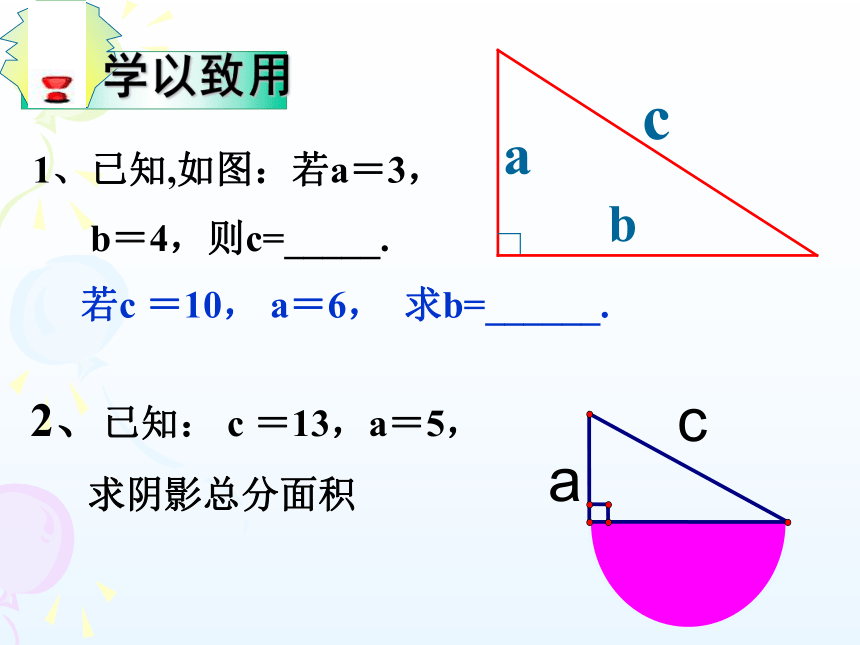
6、8、10; 1、1 根号2 9、12、15; 1、2、根号5 5、12、13; 2、3、根号13 7、24、25; 8、15、17; 1、已知,如图:若a=3,
b=4,则c=_____.
若c =10, a=6, 求b=______. 3.在? ABC中, ∠ C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 4.在? ABC中, ∠ C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.6841244.85、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
S△ABC=___.151206、已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理7、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和精选P57 8DA8、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?A4000米5000米20秒后BC 3000米探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能5、 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8----利用勾股定理求解几何体 的最短路线长 勾股定理的专题学习如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512一、台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.二、长方体中的最值问题例2、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?分析: 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短. 小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?58厘米46厘米74厘米∴售货员没搞错∵荧屏对角线大约为74厘米三、圆柱(锥)中的最值问题例3、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)4.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
AB动手试试四、正方体中的最值问题例5、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C(一)、折叠四边形例1:折叠矩形纸片,先折出折痕对角线BD,再绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE探究3数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?01234解:LAB扩展利用勾股定理作出长为
的线段.111、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
数学家、天文学家。s1s2s3
相传2500年前,古希腊著名数学家毕达哥拉斯从朋友家地砖铺成的地面上发现等腰直角三角形三边存在某种数量关系,我们来看是怎样的数量关系? s1、s2、s3、的面积有什么关系?等腰直角三角形三边有什么关系?S1+S2=S3两直角边的平方和等于斜边的平方ABC图2图3491392534sA+sB=sC两直角边的平方和
等于斜边的平方命题1:如果直角三角形的两直角边长分别为a、b,斜边
长为c,那么a2+b2=c2。abcabcabc证:s大正方形=(a+b)2=a2+2ab+b2
证:s大正方形=c2
s大正方形=c2+4× ab=c2+2ab∵s大正方形=s大正方形
∴a2+2ab+b2=c2+2ab
∴a2+b2=c2
s大正方形=4× ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2
∵s大正方形= s大正方形
∴c2=a2+b2 如果直角三角形两直角边分别为a,b,斜边为c,那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理勾股弦结论变形
c2=a2 + b21、利用数格子或计算面积的方法,探索了直角三角形的三边关系,得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2结论变形:c2=a2 + b2常见的勾股数及特殊的三边
3、4、5;
6、8、10; 1、1 根号2 9、12、15; 1、2、根号5 5、12、13; 2、3、根号13 7、24、25; 8、15、17; 1、已知,如图:若a=3,
b=4,则c=_____.
若c =10, a=6, 求b=______. 3.在? ABC中, ∠ C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 4.在? ABC中, ∠ C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.6841244.85、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
S△ABC=___.151206、已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理7、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和精选P57 8DA8、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?A4000米5000米20秒后BC 3000米探究1一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?2mDCAB连结AC,在Rt△ABC中,根据勾股定理,
因此,AC= ≈2.236
因为AC______木板的宽,
所以木板____ 从门框内通过.大于能5、 如图,盒内长,宽,高分别是30米,24米和18米,盒内可放的棍子最长是多少米?183024探究2ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?ACOBD分析:DB=OD-OB,求BD,可以 先求OB,OD.
在Rt△AOB中,梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABC 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=8----利用勾股定理求解几何体 的最短路线长 勾股定理的专题学习如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BA531512一、台阶中的最值问题∵ AB2=AC2+BC2=169,
∴ AB=13.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.二、长方体中的最值问题例2、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?分析: 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短. 小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了.你同意他的想法吗?你能解释这是为什么吗?58厘米46厘米74厘米∴售货员没搞错∵荧屏对角线大约为74厘米三、圆柱(锥)中的最值问题例3、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)4.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
AB动手试试四、正方体中的最值问题例5、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B) √5 (C)2 (D)1分析: 由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).C(一)、折叠四边形例1:折叠矩形纸片,先折出折痕对角线BD,再绕点D折叠,使点A落在BD的E处,折痕DG,若AB=2,BC=1,求AG的长。DAGBCE例2:矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。ABCDFE探究3数轴上的点有的表示有理数,有的表示
无理数,你能在数轴上画出表示 的
点吗?01234解:LAB扩展利用勾股定理作出长为
的线段.111、本节课我们经历了怎样的过程? 经历了从实际问题引入数学问题然后发现定理,再到探
索定理,最后学会验证定理及应用定理解决实际问题的过程。 2、本节课我们学到了什么? 通过本节课的学习我们不但知道了著名的勾股定理,还
知道从特殊到一般的探索方法及借助于图形的面积来探索、
验证数学结论的数形结合思想。3、学了本节课后我们有什么感想? 很多的数学结论存在于平常的生活中,需要我们用数学
的眼光去观察、思考、发现,这节课我们还受到了数学文化
辉煌历史的教育。
