18.1勾股定理(三)[下学期]
文档属性
| 名称 | 18.1勾股定理(三)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 182.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-25 00:00:00 | ||
图片预览




文档简介
课件14张PPT。2 勾股定理的应用知识回顾:1 勾股定理 的条件和结论分别是什么?2 a 、b、c分别是直角三角形的三边,则一 定有a2=c2-b2吗?
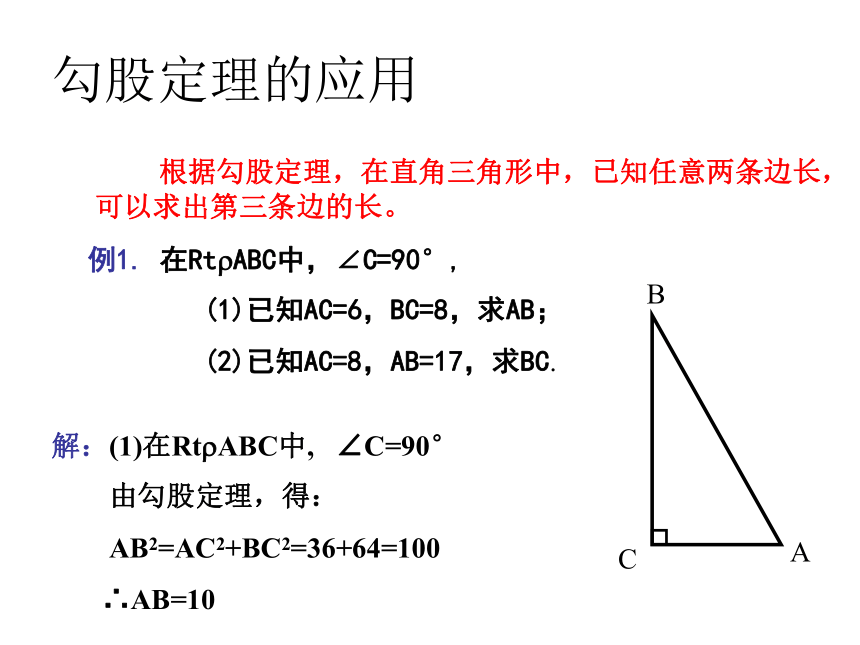
勾股定理的应用 根据勾股定理,在直角三角形中,已知任意两条边长,可以求出第三条边的长。例1. 在Rt?ABC中,∠C=90°,
(1)已知AC=6,BC=8,求AB;
(2)已知AC=8,AB=17,求BC.解:(1)在Rt?ABC中, ∠C=90°
由勾股定理,得:
AB2=AC2+BC2=36+64=100
∴AB=10 CBA在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;(3)若c=25,b=15,则 a = ;20(4)若c=10,a:b=3:4,则a=____,b=___. 68练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( )二填空??例2. 在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求
出a、b.解:设a=3x,b=4x
在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.巩固练习1.一直角三角形的一直角边长为40,斜边是41,则另一直角边为______.
2.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c, a=9,b=12,则c=______.
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕c=3﹕5,b=20.则a=______c=___.
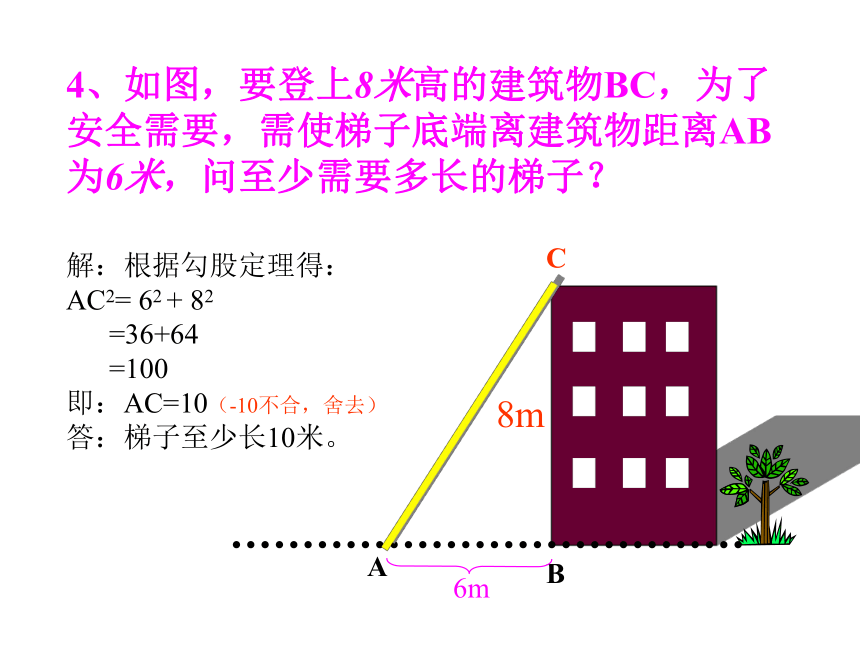
4.直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________ .9152524㎝24.8㎝154、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
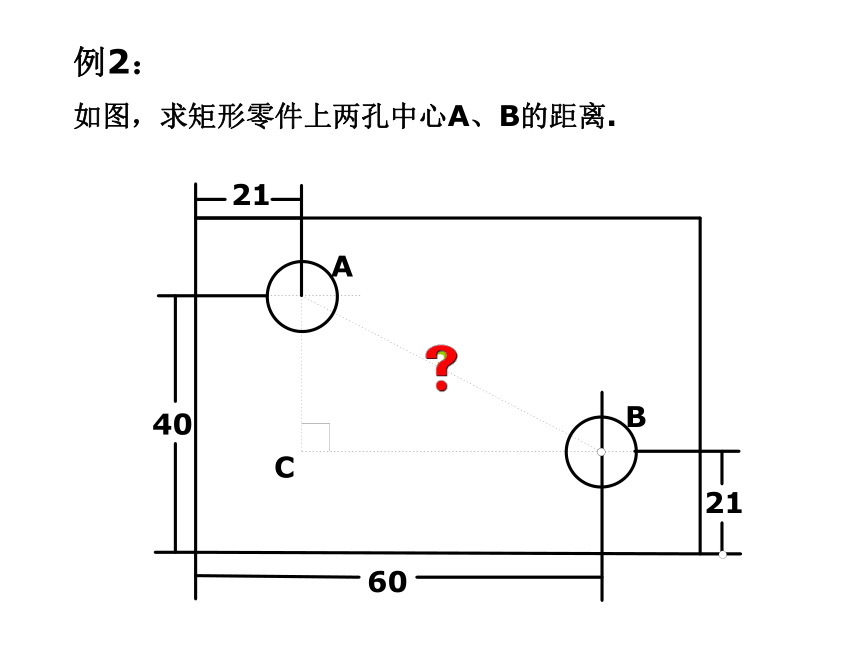
答:梯子至少长10米。例2:
如图,求矩形零件上两孔中心A、B的距离.?1、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
3、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4千米处,过了20秒,飞机距离这个男孩子头顶5千米,飞机每小时飞行多少千米?
20秒后4 km5 km如图,在Rt△ABC中,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:作如图所示上述解法正确吗?练3在一直角三角形中三边为a=3,b=4,则c= 。5或 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?练习4542.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
3.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD= .
12
勾股定理的应用 根据勾股定理,在直角三角形中,已知任意两条边长,可以求出第三条边的长。例1. 在Rt?ABC中,∠C=90°,
(1)已知AC=6,BC=8,求AB;
(2)已知AC=8,AB=17,求BC.解:(1)在Rt?ABC中, ∠C=90°
由勾股定理,得:
AB2=AC2+BC2=36+64=100
∴AB=10 CBA在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;(3)若c=25,b=15,则 a = ;20(4)若c=10,a:b=3:4,则a=____,b=___. 68练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( ) 2.? ABC的a=6,b=8,则c=10 ( )二填空??例2. 在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕b=3﹕4,c=15.求a、b.分析:通过设未知数,根据勾股定理列出方程求
出a、b.解:设a=3x,b=4x
在Rt△ABC中,∠C=90°,
由勾股定理,得:a2+b2=c2
即:9x2+16x2=225
解得:x2=9 ∴x=3(负值舍去)
∴a=9, b=12.巩固练习1.一直角三角形的一直角边长为40,斜边是41,则另一直角边为______.
2.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c, a=9,b=12,则c=______.
3.在Rt△ABC中,∠C=90°, ∠A、∠B、∠C的对边分别为a、b、c,若a﹕c=3﹕5,b=20.则a=______c=___.
4.直角三角形一直角边长为6㎝,斜边为10㎝,则这个三角形的面积为_______,斜边上的高为_________ .9152524㎝24.8㎝154、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?
8mBCA6m解:根据勾股定理得:
AC2= 62 + 82
=36+64
=100
即:AC=10(-10不合,舍去)
答:梯子至少长10米。例2:
如图,求矩形零件上两孔中心A、B的距离.?1、小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米2、如图,一根旗杆在离地面9米处断裂,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高。
3、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4千米处,过了20秒,飞机距离这个男孩子头顶5千米,飞机每小时飞行多少千米?
20秒后4 km5 km如图,在Rt△ABC中,BC=24,AC=7,求AB的长.在Rt△ABC中,根据勾股定理解:作如图所示上述解法正确吗?练3在一直角三角形中三边为a=3,b=4,则c= 。5或 思维拓展: 有没有一种直角三角形,已知一边可以求另外两边长呢?练习4542.在Rt△ABC中,∠C=90 ,∠A=30 .则BC:AC:AB=
.
3.在Rt△ABC中,∠C=90 , AC=BC.则AC :BC :AB=
. 若AB=8则AC= .
又若CD⊥AB于D,则CD= .
12
