鲁教版(五四制)数学八年级上册 5.3 三角形的中位线-第二课时 课件(共17张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 5.3 三角形的中位线-第二课时 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 18:48:01 | ||
图片预览



文档简介
(共17张PPT)
第二课时
三角形的中位线
Contents
目录
01
02
03
04
学习目标
课堂小结
合作探究
拓展练习
知识回顾
05
1.掌握定理“过三角形一边中点且平行另一边的直线平分第三边”。
2.能够应用三角形中位线概念及定理恰当添加辅助线进行有关的论证和计算,进一步提高逻辑推理能力。
D
E
A
B
C
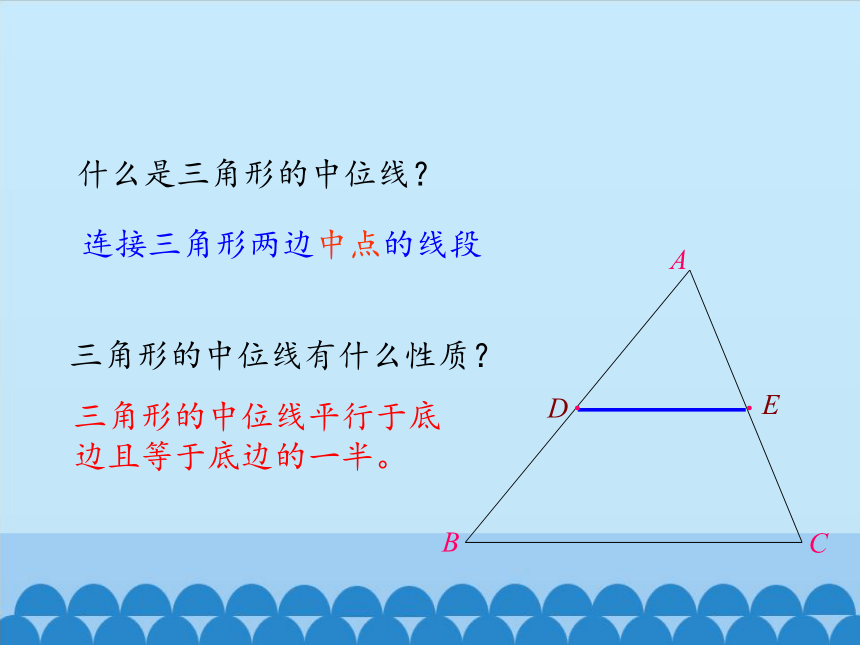
什么是三角形的中位线?
三角形的中位线平行于底边且等于底边的一半。
连接三角形两边中点的线段
三角形的中位线有什么性质?
议一议:
B
A
D
E
C
D
E
C
B
A
(1)
(2)
F
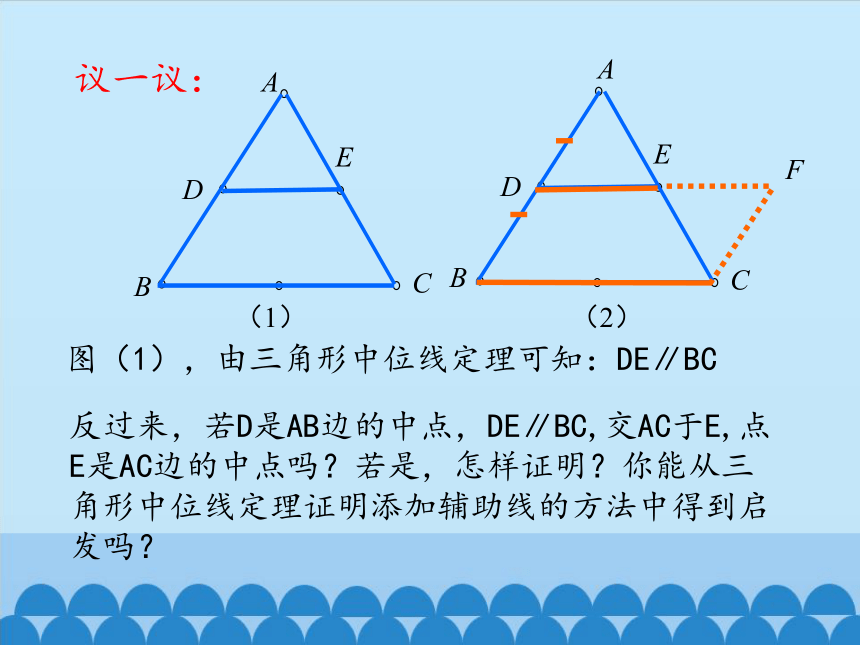
图(1),由三角形中位线定理可知:DE∥BC
反过来,若D是AB边的中点,DE∥BC,交AC于E,点E是AC边的中点吗?若是,怎样证明?你能从三角形中位线定理证明添加辅助线的方法中得到启发吗?
B
A
D
E
C
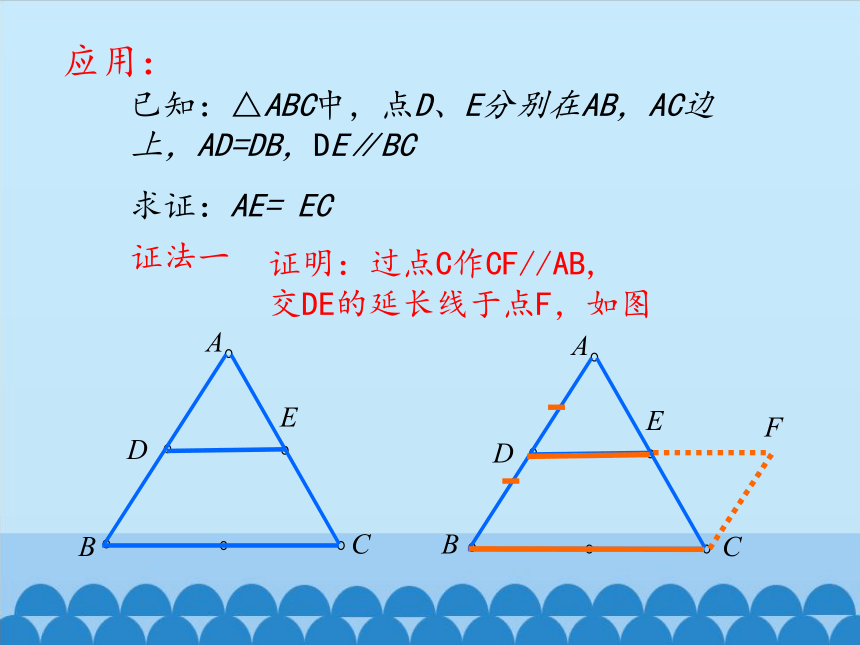
已知:△ABC中,点D、E分别在AB,AC边上,AD=DB,DE∥BC
求证:AE= EC
A
D
F
E
C
B
证法一
证明:过点C作CF//AB,
交DE的延长线于点F,如图
应用:
B
A
D
E
C
A
D
F
E
C
B
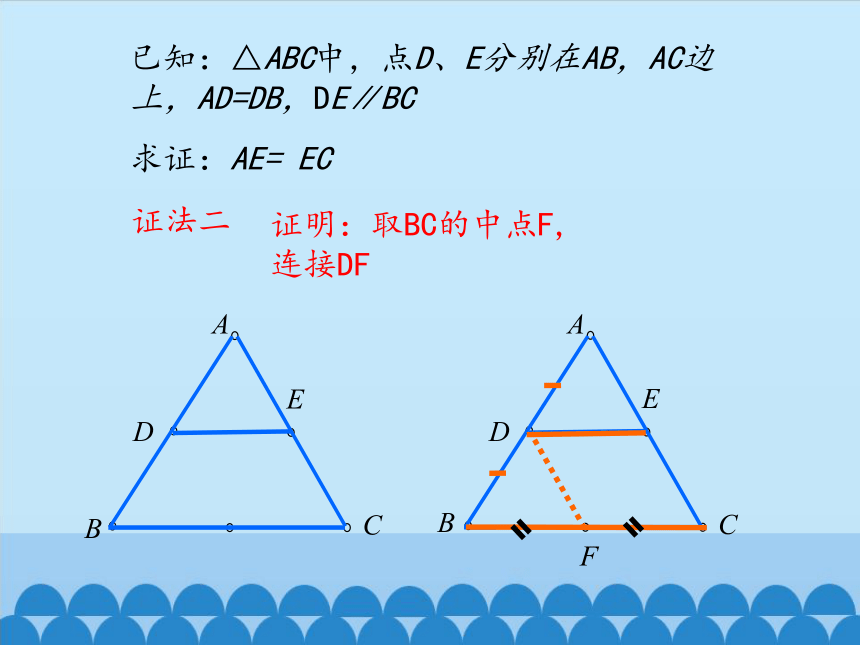
证法二
证明:取BC的中点F,
连接DF
已知:△ABC中,点D、E分别在AB,AC边上,AD=DB,DE∥BC
求证:AE= EC
B
A
D
E
C
A
D
F
E
C
B
F
作EF//AB交BC于点F
延长ED至F,使DF=DE,连接BF
A
D
F
E
C
B
随堂练习
证明:延长DE到F,使DF=BC
连接CF
A
D
F
E
C
B
证法二
证明:过点D作DF//AC,
拓展思考:由上述证明得出:经过三角形一边的中点且平行于另一边的直线,必平分三角形的第三边。你认为对吗?
F
若D是AB的中点,DE∥BC,你会
得出什么结论?
结论:
E是AC的中点
即AE=EC.
A
D
C
B
F
E
M
1.如图,在四边形ABCD中,E、M、F是中点,AD=BC。求证:∠EFM=∠FEM。
2.在三角形ABC中,AD是BC边的中线,E是AD的中点,连接BE并延长交AC与点F,用图中添加辅助线的方法。
求证:AF= FC
D
B
A
M
C
F
E
取BF的中点M,连接DM
3.如图,BE、CF是中线,并交于点G,用图中添加辅助线的方法。
求证:BG=2GE,CG=2GF。
D
B
A
F
C
E
G
延长BE使GD=BG,连接AD
4.BE、CF是中线,并交于点G,P、Q是中点,求证:(1)EFPQ是平行四边形
(2)BG=2GE,CG=2GF
P
B
A
F
C
E
G
Q
这节课我们学习了:
1.定理“过三角形一边中点且平行另一边的直线平分第三边”。
2.能够应用三角形中位线概念及定理恰当添加辅助线进行有关的论证和计算。
谢 谢
第二课时
三角形的中位线
Contents
目录
01
02
03
04
学习目标
课堂小结
合作探究
拓展练习
知识回顾
05
1.掌握定理“过三角形一边中点且平行另一边的直线平分第三边”。
2.能够应用三角形中位线概念及定理恰当添加辅助线进行有关的论证和计算,进一步提高逻辑推理能力。
D
E
A
B
C
什么是三角形的中位线?
三角形的中位线平行于底边且等于底边的一半。
连接三角形两边中点的线段
三角形的中位线有什么性质?
议一议:
B
A
D
E
C
D
E
C
B
A
(1)
(2)
F
图(1),由三角形中位线定理可知:DE∥BC
反过来,若D是AB边的中点,DE∥BC,交AC于E,点E是AC边的中点吗?若是,怎样证明?你能从三角形中位线定理证明添加辅助线的方法中得到启发吗?
B
A
D
E
C
已知:△ABC中,点D、E分别在AB,AC边上,AD=DB,DE∥BC
求证:AE= EC
A
D
F
E
C
B
证法一
证明:过点C作CF//AB,
交DE的延长线于点F,如图
应用:
B
A
D
E
C
A
D
F
E
C
B
证法二
证明:取BC的中点F,
连接DF
已知:△ABC中,点D、E分别在AB,AC边上,AD=DB,DE∥BC
求证:AE= EC
B
A
D
E
C
A
D
F
E
C
B
F
作EF//AB交BC于点F
延长ED至F,使DF=DE,连接BF
A
D
F
E
C
B
随堂练习
证明:延长DE到F,使DF=BC
连接CF
A
D
F
E
C
B
证法二
证明:过点D作DF//AC,
拓展思考:由上述证明得出:经过三角形一边的中点且平行于另一边的直线,必平分三角形的第三边。你认为对吗?
F
若D是AB的中点,DE∥BC,你会
得出什么结论?
结论:
E是AC的中点
即AE=EC.
A
D
C
B
F
E
M
1.如图,在四边形ABCD中,E、M、F是中点,AD=BC。求证:∠EFM=∠FEM。
2.在三角形ABC中,AD是BC边的中线,E是AD的中点,连接BE并延长交AC与点F,用图中添加辅助线的方法。
求证:AF= FC
D
B
A
M
C
F
E
取BF的中点M,连接DM
3.如图,BE、CF是中线,并交于点G,用图中添加辅助线的方法。
求证:BG=2GE,CG=2GF。
D
B
A
F
C
E
G
延长BE使GD=BG,连接AD
4.BE、CF是中线,并交于点G,P、Q是中点,求证:(1)EFPQ是平行四边形
(2)BG=2GE,CG=2GF
P
B
A
F
C
E
G
Q
这节课我们学习了:
1.定理“过三角形一边中点且平行另一边的直线平分第三边”。
2.能够应用三角形中位线概念及定理恰当添加辅助线进行有关的论证和计算。
谢 谢
