18.1勾股定理的逆定理(2)[下学期]
文档属性
| 名称 | 18.1勾股定理的逆定理(2)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 712.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-25 00:00:00 | ||
图片预览






文档简介
课件17张PPT。勾股定理的逆定理(2)1判定一个三角形是否直角三角形有几种方法回顾方法一:可以根据角度方法二:如果三角形的三边长a,b,c满足那么这个三角形是直角三角形满足 的三个 ,称为勾股数。正整数你能写出常用的勾股数3,4,5 ; 5,12,13; 8,15,17 ; 7,24,25約公元前 1700 年,巴比倫人經已發現了此定理!请你与你的同伴合作,看看可以找出多少组勾股数。勾股数满足勾股定理的数组称为勾股数(或商高数)
毕达哥拉斯学派明确地给出了勾股数的一组公式:一组勾股数的正整数解:a=2n+1,b=2n2+2n,c=2n2+2n+1,其特点是斜边与其中一股的差为1。
古希腊学者柏拉图(Plato,约前427-前347)也给了另一组公式:a=2n,b=n2-1,c=n2+1,此时斜边与其中一股之差为2。 我国古代数学巨著《九章算术》
中,也提出了一组求勾股数的式子,
这组式子相当于:任意给定两个
正整数m,n(m>n),那么这三个
正整数就是一个整勾股数组。公元3世纪,我国著名数学家刘徽从
几何上也证明了这一结论。 被誉为“代数学鼻祖”的数学家丢番图(Diophantus,约330-246)全部解的公式是a=2mn,y=m2-n2,z=m2+n2 ,其中m,n(m>n)是互质且一奇一偶的任意正整数。
1945年,人们在对古巴比伦人遗留下的一块数学泥板的研究中,惊讶地发现上面竟然刻有15组勾股数,其年代远在商高和毕达哥拉斯之前,大约在公元前1900年到公元前l600年之间。
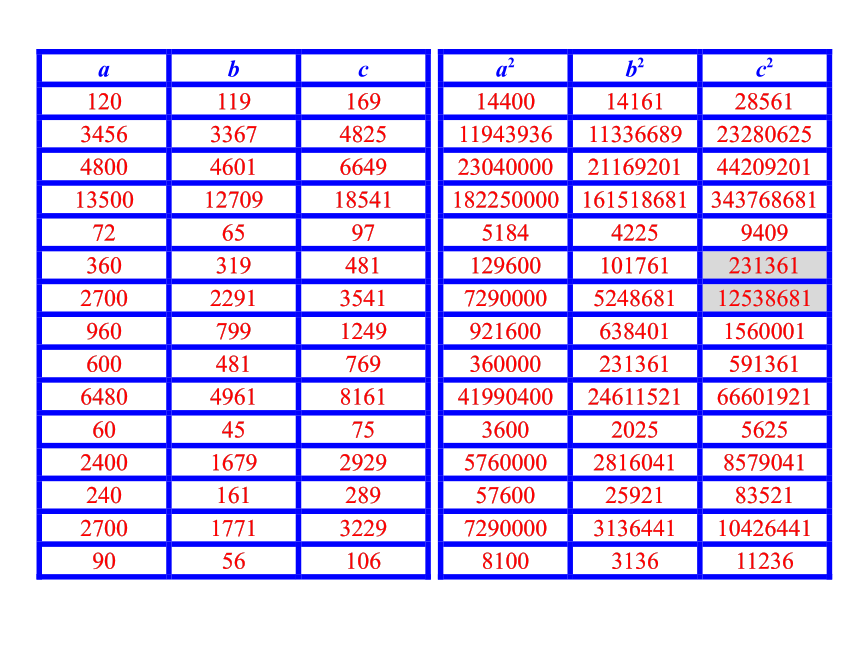
观察下列表格:请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1则a,b,c,为
基本勾数如:3、4、5;5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、若a,b,c是一组基本的勾股数,则a,b,c
不能同时为奇数或同时为偶数
4、一组勾股数中必有一个数是5倍数
5、2mn,m2-n2,m2+n2为勾股数组,m>n﹥0
,m,n一奇一偶
请找出1到50(包括50)的自然数中的数.共有几组?说说你的方法?勾股定理的推广:费尔马大定理(费尔马是17世纪法国数学家 )
广勾股定理除了三元二次方程x2 + y2 =z2(其中x、y、z都是未知数)
有正整数解以外,其他的三元n次方程xn + yn =zn
(n为已知正整数,且n>2)都不可能有正整数解。 (1)锐角对边的平方,等于其他两边之平方和,减去这两边
中的一边和另一边在这边上的射影乘积的两倍.
(2)钝角对边的平方等于其他两边的平方和,加上这两边中
的一边与另一边在这边上的射影乘积的两倍. 7.如图,有一块地,已知,AD=4m,
CD=3m,∠ADE=90°,AB=13m,
BC=12m。求这块地的面积。1.如图,两个正方形的面积分别为64,49,则AC=( )2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是( )? 说一说 ? 1.如图,∠A=∠D=90O,AB=CD=12cm,AD=BC=25cm,E是AD上一点,且AE:ED=16:9。试判断∠BEC是直角,并说明理由。? 直角三角形三边上的等边三角形的面积之间有什么关系?? 想一想 ? 图1图2△如图1,分析:由结论中的平方能联想到什么?勾股定理适用于直角三角形,构造直角三角形是关键。如何构造呢?
毕达哥拉斯学派明确地给出了勾股数的一组公式:一组勾股数的正整数解:a=2n+1,b=2n2+2n,c=2n2+2n+1,其特点是斜边与其中一股的差为1。
古希腊学者柏拉图(Plato,约前427-前347)也给了另一组公式:a=2n,b=n2-1,c=n2+1,此时斜边与其中一股之差为2。 我国古代数学巨著《九章算术》
中,也提出了一组求勾股数的式子,
这组式子相当于:任意给定两个
正整数m,n(m>n),那么这三个
正整数就是一个整勾股数组。公元3世纪,我国著名数学家刘徽从
几何上也证明了这一结论。 被誉为“代数学鼻祖”的数学家丢番图(Diophantus,约330-246)全部解的公式是a=2mn,y=m2-n2,z=m2+n2 ,其中m,n(m>n)是互质且一奇一偶的任意正整数。
1945年,人们在对古巴比伦人遗留下的一块数学泥板的研究中,惊讶地发现上面竟然刻有15组勾股数,其年代远在商高和毕达哥拉斯之前,大约在公元前1900年到公元前l600年之间。
观察下列表格:请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
勾股小常识:勾股数
1、 a2+b2 =c2,满足(a,b,c)=1则a,b,c,为
基本勾数如:3、4、5;5、12、 13;
7、24、25……
2、如果a,b,c是一组勾股数,则ka、kb、
kc(k为正整数)也是一组勾股数,如:
6、8、10;9、12、15……
3、若a,b,c是一组基本的勾股数,则a,b,c
不能同时为奇数或同时为偶数
4、一组勾股数中必有一个数是5倍数
5、2mn,m2-n2,m2+n2为勾股数组,m>n﹥0
,m,n一奇一偶
请找出1到50(包括50)的自然数中的数.共有几组?说说你的方法?勾股定理的推广:费尔马大定理(费尔马是17世纪法国数学家 )
广勾股定理除了三元二次方程x2 + y2 =z2(其中x、y、z都是未知数)
有正整数解以外,其他的三元n次方程xn + yn =zn
(n为已知正整数,且n>2)都不可能有正整数解。 (1)锐角对边的平方,等于其他两边之平方和,减去这两边
中的一边和另一边在这边上的射影乘积的两倍.
(2)钝角对边的平方等于其他两边的平方和,加上这两边中
的一边与另一边在这边上的射影乘积的两倍. 7.如图,有一块地,已知,AD=4m,
CD=3m,∠ADE=90°,AB=13m,
BC=12m。求这块地的面积。1.如图,两个正方形的面积分别为64,49,则AC=( )2.由四根木棒,长度分别为3,4,5,6
若去其中三根木棒组呈三角形,有( )
中取法,其中,能构成直角三角形的是( )? 说一说 ? 1.如图,∠A=∠D=90O,AB=CD=12cm,AD=BC=25cm,E是AD上一点,且AE:ED=16:9。试判断∠BEC是直角,并说明理由。? 直角三角形三边上的等边三角形的面积之间有什么关系?? 想一想 ? 图1图2△如图1,分析:由结论中的平方能联想到什么?勾股定理适用于直角三角形,构造直角三角形是关键。如何构造呢?
