沪科版八年级上册全等三角形的判定第2讲手拉手模型 课件(16张PPT)
文档属性
| 名称 | 沪科版八年级上册全等三角形的判定第2讲手拉手模型 课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 28.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 08:23:21 | ||
图片预览


文档简介
(共16张PPT)
八年级全等模型汇总
第2讲 手拉手模型
八年级全等模型汇总
2、手拉手模型-定义
【知识梳理】
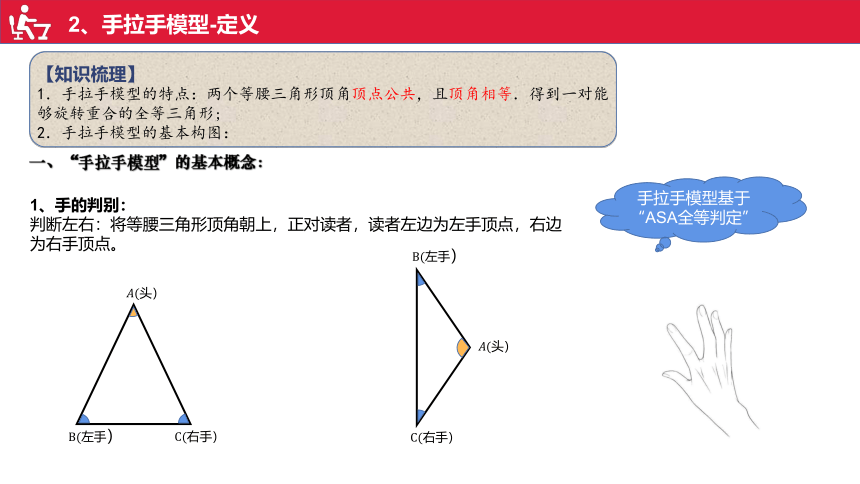
1.手拉手模型的特点:两个等腰三角形顶角顶点公共,且顶角相等.得到一对能够旋转重合的全等三角形;
2.手拉手模型的基本构图:
一、“手拉手模型”的基本概念:
1、手的判别:
判断左右:将等腰三角形顶角朝上,正对读者,读者左边为左手顶点,右边为右手顶点。
)
)
)
)
)
)
手拉手模型基于“ASA全等判定”
2、手拉手模型-模型分析
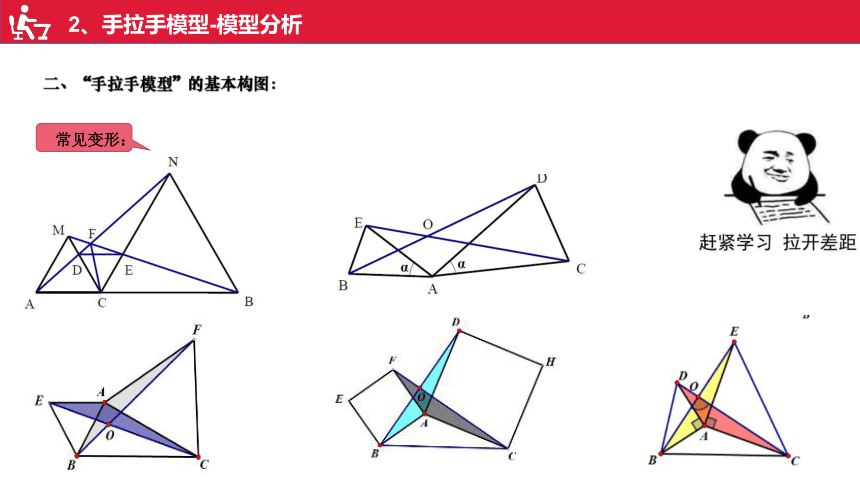
二、“手拉手模型”的基本构图:
常见变形:
手拉手模型-等边三角形
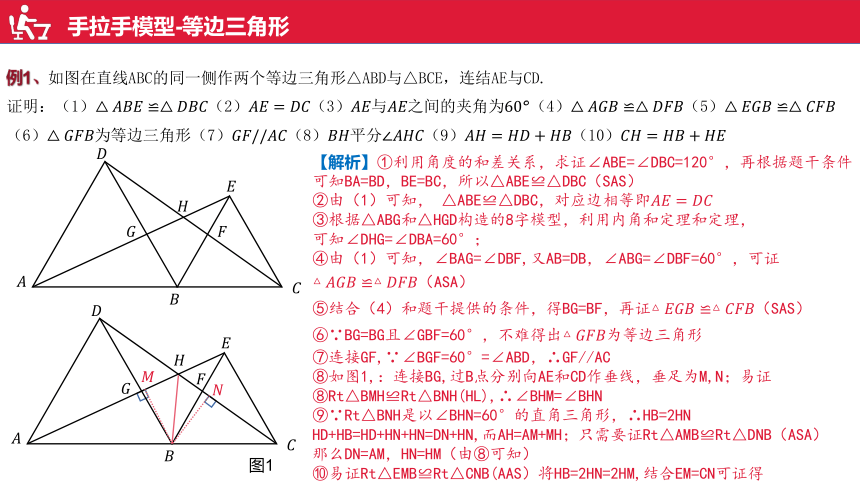
例1、如图在直线ABC的同一侧作两个等边三角形△ABD与△BCE,连结AE与CD.
证明:(1)(2)(3)与之间的夹角为(4)(5)(6)为等边三角形(7)(8)平分(9)(10)
【解析】①利用角度的和差关系,求证∠ABE=∠DBC=120°,再根据题干条件
可知BA=BD,BE=BC,所以△ABE≌△DBC(SAS)
②由(1)可知, △ABE≌△DBC,对应边相等即
③根据△ABG和△HGD构造的8字模型,利用内角和定理和定理,
可知∠DHG=∠DBA=60°;
④由(1)可知,∠BAG=∠DBF,又AB=DB,∠ABG=∠DBF=60°,可证
(ASA)
⑤结合(4)和题干提供的条件,得BG=BF,再证(SAS)
⑥∵BG=BG且∠GBF=60°,不难得出为等边三角形
⑦连接GF,∵∠BGF=60°=∠ABD,∴GF//AC
⑧如图1,:连接BG,过B点分别向AE和CD作垂线,垂足为M,N;易证
⑧Rt△BMH≌Rt△BNH(HL),∴∠BHM=∠BHN
⑨∵Rt△BNH是以∠BHN=60°的直角三角形,∴HB=2HN
HD+HB=HD+HN+HN=DN+HN,而AH=AM+MH;只需要证Rt△AMB≌Rt△DNB(ASA)
那么DN=AM,HN=HM(由⑧可知)
⑩易证Rt△EMB≌Rt△CNB(AAS)将HB=2HN=2HM,结合EM=CN可证得
1
手拉手模型-等边三角形
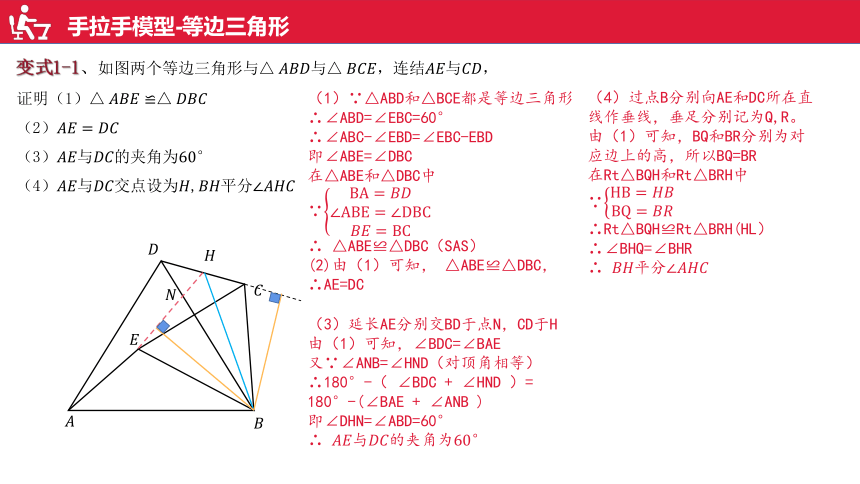
变式1-1、如图两个等边三角形与与,连结与,
证明(1)
(2)
(3)与的夹角为
(4)与交点设为,平分
(1)∵△ABD和△BCE都是等边三角形
∴∠ABD=∠EBC=60°
∴∠ABC-∠EBD=∠EBC-EBD
即∠ABE=∠DBC
在△ABE和△DBC中
∵
∴ △ABE≌△DBC(SAS)
(2)由(1)可知, △ABE≌△DBC,
∴AE=DC
(3)延长AE分别交BD于点N,CD于H
由(1)可知,∠BDC=∠BAE
又∵∠ANB=∠HND(对顶角相等)
∴180°-( ∠BDC + ∠HND )=
180°-(∠BAE + ∠ANB )
即∠DHN=∠ABD=60°
∴ 与的夹角为°
(4)过点B分别向AE和DC所在直线作垂线,垂足分别记为Q,R。
由(1)可知,BQ和BR分别为对应边上的高,所以BQ=BR
在Rt△BQH和Rt△BRH中
∵
∴Rt△BQH≌Rt△BRH(HL)
∴∠BHQ=∠BHR
∴ 平分
手拉手模型-等边三角形
变式1-2.如图,三角形ABC和三角形CDE都是等边三角形,点A,E,D,同在一条直线上,且∠EBD=62°,求∠AEB的度数
解:
∵∠AEB=62°
∴∠BDE+∠BED=180°-∠AEB=180°-62°=112°
又∵∠DCB=60°-∠BCE,∠ACE=60°-∠BCE
∴∠DCB=∠ACE
在△BDC和△ACE中
∵
∴△BDC≌△ACE(SAS)
∴∠AEC=∠BDC=∠EDC+∠BDE=60°+∠BDE
∴∠AED=360°-(∠BED+∠DEC+∠AEC)
=360°-(∠BED+∠EDC+∠60°+∠BDE)
=360°-(112°+60°+60°)=122°
手拉手模型-等边三角形
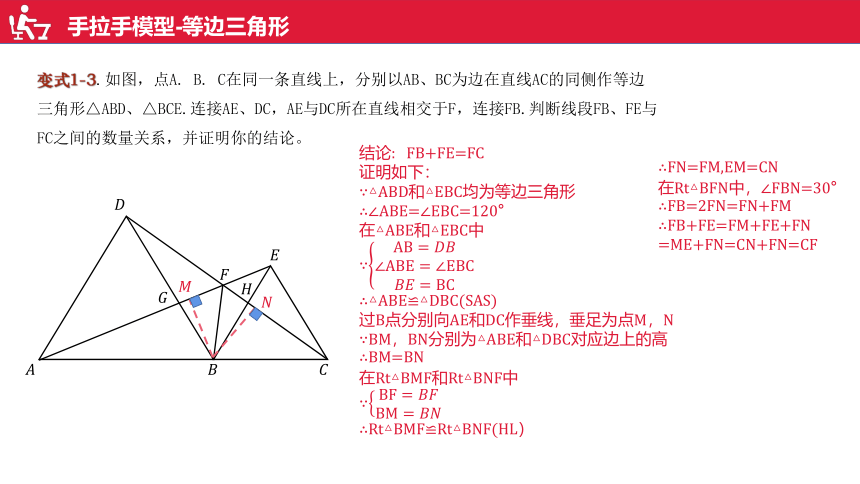
变式1-3. 如图,点A. B. C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论。
结论: FB+FE=FC
证明如下:
∵△ABD和△EBC均为等边三角形
∴∠ABE=∠EBC=120°
在△ABE和△EBC中
∵
∴△ABE≌△DBC(SAS)
过B点分别向AE和DC作垂线,垂足为点M,N
∵BM,BN分别为△ABE和△DBC对应边上的高
∴BM=BN
在Rt△BMF和Rt△BNF中
∵
∴Rt△BMF≌Rt△BNF(HL)
∴FN=FM,EM=CN
在Rt△BFN中,∠FBN=30°
∴FB=2FN=FN+FM
∴FB+FE=FM+FE+FN
=ME+FN=CN+FN=CF
手拉手模型-等边三角形
变式1-4.
如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
1. △ABE≌△DBC
2. AE=DC
3. AE与DC的夹角为60°
4. AE与DC的交点设为H,BH平分∠AHC
【解析】①利用角度的和差关系证明∠ABE=∠DBC,且AB=DB,BC=BE
证明△ABE≌△DBC(SAS)
②由①可知,对应边相等
③∵∠BAE=∠BDC,∴∠HAD+∠ADH=60°-∠BAE+60°+∠BDC=120°
∴∠AHD=60°(利用△AHD的内角和等于180°)
④连接BH,只需要过点H分别在AE和CD上作高,构造以BH公共斜边的全等直角三角形,再利用对应角相等
例2、如图,两个正方形与,连结,二者相交于点
证明:(1)(2)(3)(4)平分
手拉手模型-共轭正方形
【解析】(1)∵∠ADG=90°+∠CDG,∠CDE=90°+∠CDG
∴∠ADG=∠CDE
在△ADG和△CDE中
∵
∴ △ADG≌△CDE(SAS)
(2)由(1)可知△ADG≌△CDE,∴AG=CE
(3)令AG与CD交点为Q,
∵∠CQH=∠DQA,∠DAG=∠DCE
∴180°-( ∠CQH + ∠DCE )=180°-(∠DQA+ ∠DAG)
即∠GHC=∠ADC=90°,∴AG⊥CE
(4)连接HD,过D点分别作AG和CE上的高,垂足为R,S
易证Rt△DRH≌Rt△DSH(HL)
∴∠DHR=∠DHS
∴ 平分
手拉手模型-共轭正方形
变式2-1.
如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H.
问 (1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
【解析】
(1)利用角度的和差关系,手拉手全等(SAS)
(2)由(1)中的全等关系可证
(3)利用八字模型,三角形内角和定理得到夹角等于90°
(4)连接HD,过D点分别作AG和CE上的高,构造以HD为
公共斜边的直角三角形,进而求证∠DHA=∠DHE
HD平分∠AHE
手拉手模型-共轭正方形
变式2-2.如图,以△ABC的边AC,AB为一边,分别向三角形的外侧作正方形ACFG和正方形ABDE,连接EC交AB于点H,连接BG交CE于点M.
(1)求证:BG⊥CE
(2)连接EG,求证:△ABC与△AGE面积相等
【解析】
(1)①先利用手拉手模型,求证△EAC≌△BAG(SAS)
再根据以M,C,A,G形成的八字模型,求得∠GMC=∠CAG=90°
(2)不难发现,∠GAE与∠BAC互补,且AG=AC,AE=AB
利用表示,具体可参考下图
手拉手模型-共轭正方形
变式2-3.如图,在△ABC的外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连接DC、BE交于F点.
(1)求证:△DAC≌△BAE
(2)直线DC、BE是否互相垂直,请说明理由
(3)求证:AF平分∠DFE
【解析】①先利用角度和差关系,求证∠DAC=∠BAE
再根据题干条件AD=AB,AC=AE
∴△DAC≌△BAE(SAS)
②利用点D,A,B,F构造的八字模型,求得∠DFB=∠DAB=90°
③过点A分别作DC和BE上的高,利用HL的判定,证全等;再根据对应角相等
∴AF平分∠DFE
手拉手模型-锐角等腰三角形
例3、如图,在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于点O.
(1)求证:BE=CF(2)当∠BAC=70°时,求∠BAC=70°时,求∠BOC的度数
(1)证明:∵∠CAB=∠EAF
∴ ∠CAB+∠CAE=∠EAF+∠CAE
即∠BAE=∠CAF
在△BAE和△CAF中
∵
∴ △BAE≌△CAF(SAS)
∴BE=CF
(2)当∠BAC=70°
由(1)可知△BAE≌△CAF
∴∠EBA=∠ACF
又∵∠CDO=∠ADB
∴180°-(∠EBA+ ∠ADB )=180°-( ∠ACF +∠CDO)
即∠BOC=∠BAC=70°
手拉手模型-解答题压轴
例4如图(1),已知△ABC和△AED均为等腰三角形,AB=AC,AD=AE,且∠BAC=∠EAD.
1
2
(1)求证:CD=BE;
(2)将△ABC绕点A旋转到如图(2)的位置,(1)中的结论仍然成立吗?证明你的结论
(3)如图(2),连接EC,若点P是EC的中点,连接PB并延长至点F,使CF=CD,求证:∠EBP=∠BFC
【解析】①连接CD,易证△EAB≌△DCA(SAS),∴CD=BE
②方法如例1,利用角度的和差关系,先证一条件:∠EAB=∠DAC
③题干中P是EC中点,是解题的题眼;我们可以倍长中线,构造△EPH≌△CPF(SAS)
∴CF=HE 由(1)可知CF=CD=EB
∴△HEB是等腰三角形 ,最后证得∠EBP=∠BFC
倍长中线
手拉手模型-解答题压轴
1
2
3
例5如图1,在△ABC中,AE⊥BC于点E,AE=BE,连接BD,CD
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,请直接写出结论;
②你能求出BD与AC的夹角度数吗 如果能,请直接写出夹角度数;如果不能,请说明理由.
(1) BD⊥AC
(2) BD与AC互相垂直,且长度相等
(3) 手拉手模型的基础应用
开动脑筋,试试吧
手拉手模型-解答题压轴
例6 (1)【问题背景】如图(1),∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE. 求证:BD=CE;
(2)【问题探究】将图(1)中△DAE绕着点A旋转,使点D落在△ABC内部,如图(2),其余条件不变,请
探究BD与CE的关系(数量关系和位置关系),并证明你的结论;
(3)【拓展应用】连接图(1)中CD,BE,如图(3),若BD=8,请直接写出四边形BCDE的面积。
(1)
(2)
(3)
①②前两问:先根据角度的和差关系,证得△BAD≌△CAE(SAS)BD=CE,再根据八字模型,BD⊥CE
③ 由①②可知,BD=EC=8,且BD⊥CE ,∴32.
八年级全等模型汇总
第2讲 手拉手模型
八年级全等模型汇总
2、手拉手模型-定义
【知识梳理】
1.手拉手模型的特点:两个等腰三角形顶角顶点公共,且顶角相等.得到一对能够旋转重合的全等三角形;
2.手拉手模型的基本构图:
一、“手拉手模型”的基本概念:
1、手的判别:
判断左右:将等腰三角形顶角朝上,正对读者,读者左边为左手顶点,右边为右手顶点。
)
)
)
)
)
)
手拉手模型基于“ASA全等判定”
2、手拉手模型-模型分析
二、“手拉手模型”的基本构图:
常见变形:
手拉手模型-等边三角形
例1、如图在直线ABC的同一侧作两个等边三角形△ABD与△BCE,连结AE与CD.
证明:(1)(2)(3)与之间的夹角为(4)(5)(6)为等边三角形(7)(8)平分(9)(10)
【解析】①利用角度的和差关系,求证∠ABE=∠DBC=120°,再根据题干条件
可知BA=BD,BE=BC,所以△ABE≌△DBC(SAS)
②由(1)可知, △ABE≌△DBC,对应边相等即
③根据△ABG和△HGD构造的8字模型,利用内角和定理和定理,
可知∠DHG=∠DBA=60°;
④由(1)可知,∠BAG=∠DBF,又AB=DB,∠ABG=∠DBF=60°,可证
(ASA)
⑤结合(4)和题干提供的条件,得BG=BF,再证(SAS)
⑥∵BG=BG且∠GBF=60°,不难得出为等边三角形
⑦连接GF,∵∠BGF=60°=∠ABD,∴GF//AC
⑧如图1,:连接BG,过B点分别向AE和CD作垂线,垂足为M,N;易证
⑧Rt△BMH≌Rt△BNH(HL),∴∠BHM=∠BHN
⑨∵Rt△BNH是以∠BHN=60°的直角三角形,∴HB=2HN
HD+HB=HD+HN+HN=DN+HN,而AH=AM+MH;只需要证Rt△AMB≌Rt△DNB(ASA)
那么DN=AM,HN=HM(由⑧可知)
⑩易证Rt△EMB≌Rt△CNB(AAS)将HB=2HN=2HM,结合EM=CN可证得
1
手拉手模型-等边三角形
变式1-1、如图两个等边三角形与与,连结与,
证明(1)
(2)
(3)与的夹角为
(4)与交点设为,平分
(1)∵△ABD和△BCE都是等边三角形
∴∠ABD=∠EBC=60°
∴∠ABC-∠EBD=∠EBC-EBD
即∠ABE=∠DBC
在△ABE和△DBC中
∵
∴ △ABE≌△DBC(SAS)
(2)由(1)可知, △ABE≌△DBC,
∴AE=DC
(3)延长AE分别交BD于点N,CD于H
由(1)可知,∠BDC=∠BAE
又∵∠ANB=∠HND(对顶角相等)
∴180°-( ∠BDC + ∠HND )=
180°-(∠BAE + ∠ANB )
即∠DHN=∠ABD=60°
∴ 与的夹角为°
(4)过点B分别向AE和DC所在直线作垂线,垂足分别记为Q,R。
由(1)可知,BQ和BR分别为对应边上的高,所以BQ=BR
在Rt△BQH和Rt△BRH中
∵
∴Rt△BQH≌Rt△BRH(HL)
∴∠BHQ=∠BHR
∴ 平分
手拉手模型-等边三角形
变式1-2.如图,三角形ABC和三角形CDE都是等边三角形,点A,E,D,同在一条直线上,且∠EBD=62°,求∠AEB的度数
解:
∵∠AEB=62°
∴∠BDE+∠BED=180°-∠AEB=180°-62°=112°
又∵∠DCB=60°-∠BCE,∠ACE=60°-∠BCE
∴∠DCB=∠ACE
在△BDC和△ACE中
∵
∴△BDC≌△ACE(SAS)
∴∠AEC=∠BDC=∠EDC+∠BDE=60°+∠BDE
∴∠AED=360°-(∠BED+∠DEC+∠AEC)
=360°-(∠BED+∠EDC+∠60°+∠BDE)
=360°-(112°+60°+60°)=122°
手拉手模型-等边三角形
变式1-3. 如图,点A. B. C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论。
结论: FB+FE=FC
证明如下:
∵△ABD和△EBC均为等边三角形
∴∠ABE=∠EBC=120°
在△ABE和△EBC中
∵
∴△ABE≌△DBC(SAS)
过B点分别向AE和DC作垂线,垂足为点M,N
∵BM,BN分别为△ABE和△DBC对应边上的高
∴BM=BN
在Rt△BMF和Rt△BNF中
∵
∴Rt△BMF≌Rt△BNF(HL)
∴FN=FM,EM=CN
在Rt△BFN中,∠FBN=30°
∴FB=2FN=FN+FM
∴FB+FE=FM+FE+FN
=ME+FN=CN+FN=CF
手拉手模型-等边三角形
变式1-4.
如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
1. △ABE≌△DBC
2. AE=DC
3. AE与DC的夹角为60°
4. AE与DC的交点设为H,BH平分∠AHC
【解析】①利用角度的和差关系证明∠ABE=∠DBC,且AB=DB,BC=BE
证明△ABE≌△DBC(SAS)
②由①可知,对应边相等
③∵∠BAE=∠BDC,∴∠HAD+∠ADH=60°-∠BAE+60°+∠BDC=120°
∴∠AHD=60°(利用△AHD的内角和等于180°)
④连接BH,只需要过点H分别在AE和CD上作高,构造以BH公共斜边的全等直角三角形,再利用对应角相等
例2、如图,两个正方形与,连结,二者相交于点
证明:(1)(2)(3)(4)平分
手拉手模型-共轭正方形
【解析】(1)∵∠ADG=90°+∠CDG,∠CDE=90°+∠CDG
∴∠ADG=∠CDE
在△ADG和△CDE中
∵
∴ △ADG≌△CDE(SAS)
(2)由(1)可知△ADG≌△CDE,∴AG=CE
(3)令AG与CD交点为Q,
∵∠CQH=∠DQA,∠DAG=∠DCE
∴180°-( ∠CQH + ∠DCE )=180°-(∠DQA+ ∠DAG)
即∠GHC=∠ADC=90°,∴AG⊥CE
(4)连接HD,过D点分别作AG和CE上的高,垂足为R,S
易证Rt△DRH≌Rt△DSH(HL)
∴∠DHR=∠DHS
∴ 平分
手拉手模型-共轭正方形
变式2-1.
如图两个等腰直角三角形ADC与EDG,连接AG,CE,二者相交于H.
问 (1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
【解析】
(1)利用角度的和差关系,手拉手全等(SAS)
(2)由(1)中的全等关系可证
(3)利用八字模型,三角形内角和定理得到夹角等于90°
(4)连接HD,过D点分别作AG和CE上的高,构造以HD为
公共斜边的直角三角形,进而求证∠DHA=∠DHE
HD平分∠AHE
手拉手模型-共轭正方形
变式2-2.如图,以△ABC的边AC,AB为一边,分别向三角形的外侧作正方形ACFG和正方形ABDE,连接EC交AB于点H,连接BG交CE于点M.
(1)求证:BG⊥CE
(2)连接EG,求证:△ABC与△AGE面积相等
【解析】
(1)①先利用手拉手模型,求证△EAC≌△BAG(SAS)
再根据以M,C,A,G形成的八字模型,求得∠GMC=∠CAG=90°
(2)不难发现,∠GAE与∠BAC互补,且AG=AC,AE=AB
利用表示,具体可参考下图
手拉手模型-共轭正方形
变式2-3.如图,在△ABC的外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连接DC、BE交于F点.
(1)求证:△DAC≌△BAE
(2)直线DC、BE是否互相垂直,请说明理由
(3)求证:AF平分∠DFE
【解析】①先利用角度和差关系,求证∠DAC=∠BAE
再根据题干条件AD=AB,AC=AE
∴△DAC≌△BAE(SAS)
②利用点D,A,B,F构造的八字模型,求得∠DFB=∠DAB=90°
③过点A分别作DC和BE上的高,利用HL的判定,证全等;再根据对应角相等
∴AF平分∠DFE
手拉手模型-锐角等腰三角形
例3、如图,在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于点O.
(1)求证:BE=CF(2)当∠BAC=70°时,求∠BAC=70°时,求∠BOC的度数
(1)证明:∵∠CAB=∠EAF
∴ ∠CAB+∠CAE=∠EAF+∠CAE
即∠BAE=∠CAF
在△BAE和△CAF中
∵
∴ △BAE≌△CAF(SAS)
∴BE=CF
(2)当∠BAC=70°
由(1)可知△BAE≌△CAF
∴∠EBA=∠ACF
又∵∠CDO=∠ADB
∴180°-(∠EBA+ ∠ADB )=180°-( ∠ACF +∠CDO)
即∠BOC=∠BAC=70°
手拉手模型-解答题压轴
例4如图(1),已知△ABC和△AED均为等腰三角形,AB=AC,AD=AE,且∠BAC=∠EAD.
1
2
(1)求证:CD=BE;
(2)将△ABC绕点A旋转到如图(2)的位置,(1)中的结论仍然成立吗?证明你的结论
(3)如图(2),连接EC,若点P是EC的中点,连接PB并延长至点F,使CF=CD,求证:∠EBP=∠BFC
【解析】①连接CD,易证△EAB≌△DCA(SAS),∴CD=BE
②方法如例1,利用角度的和差关系,先证一条件:∠EAB=∠DAC
③题干中P是EC中点,是解题的题眼;我们可以倍长中线,构造△EPH≌△CPF(SAS)
∴CF=HE 由(1)可知CF=CD=EB
∴△HEB是等腰三角形 ,最后证得∠EBP=∠BFC
倍长中线
手拉手模型-解答题压轴
1
2
3
例5如图1,在△ABC中,AE⊥BC于点E,AE=BE,连接BD,CD
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,请直接写出结论;
②你能求出BD与AC的夹角度数吗 如果能,请直接写出夹角度数;如果不能,请说明理由.
(1) BD⊥AC
(2) BD与AC互相垂直,且长度相等
(3) 手拉手模型的基础应用
开动脑筋,试试吧
手拉手模型-解答题压轴
例6 (1)【问题背景】如图(1),∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE. 求证:BD=CE;
(2)【问题探究】将图(1)中△DAE绕着点A旋转,使点D落在△ABC内部,如图(2),其余条件不变,请
探究BD与CE的关系(数量关系和位置关系),并证明你的结论;
(3)【拓展应用】连接图(1)中CD,BE,如图(3),若BD=8,请直接写出四边形BCDE的面积。
(1)
(2)
(3)
①②前两问:先根据角度的和差关系,证得△BAD≌△CAE(SAS)BD=CE,再根据八字模型,BD⊥CE
③ 由①②可知,BD=EC=8,且BD⊥CE ,∴32.
