鲁教版(五四制)数学八年级上册 4.2 图形旋转性质的应用教案
文档属性
| 名称 | 鲁教版(五四制)数学八年级上册 4.2 图形旋转性质的应用教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 20:30:32 | ||
图片预览


文档简介
《旋转的应用—半角模型》教学设计
【教学目标】
结合数学课程标准和学科德育一体化要求,围绕“目标—--评价—--教学”一致性原则,确定本课教学目标如下:
1.明确半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
2.在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
3. 通过讨论交流、合作探究等活动,积累数学活动经验,培养数学学科的严谨思维和理性精神。
【教学重点】
明确半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
【教学难点】
在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
【教学过程】
情境引入
之前,我们学习过图形的变换主要有哪些形式 平移、旋转和轴对称。其中旋转式我们解决几何问题的一大利器。今天我们就来探究如何利用旋转来解决半角模型问题(板书课题)。
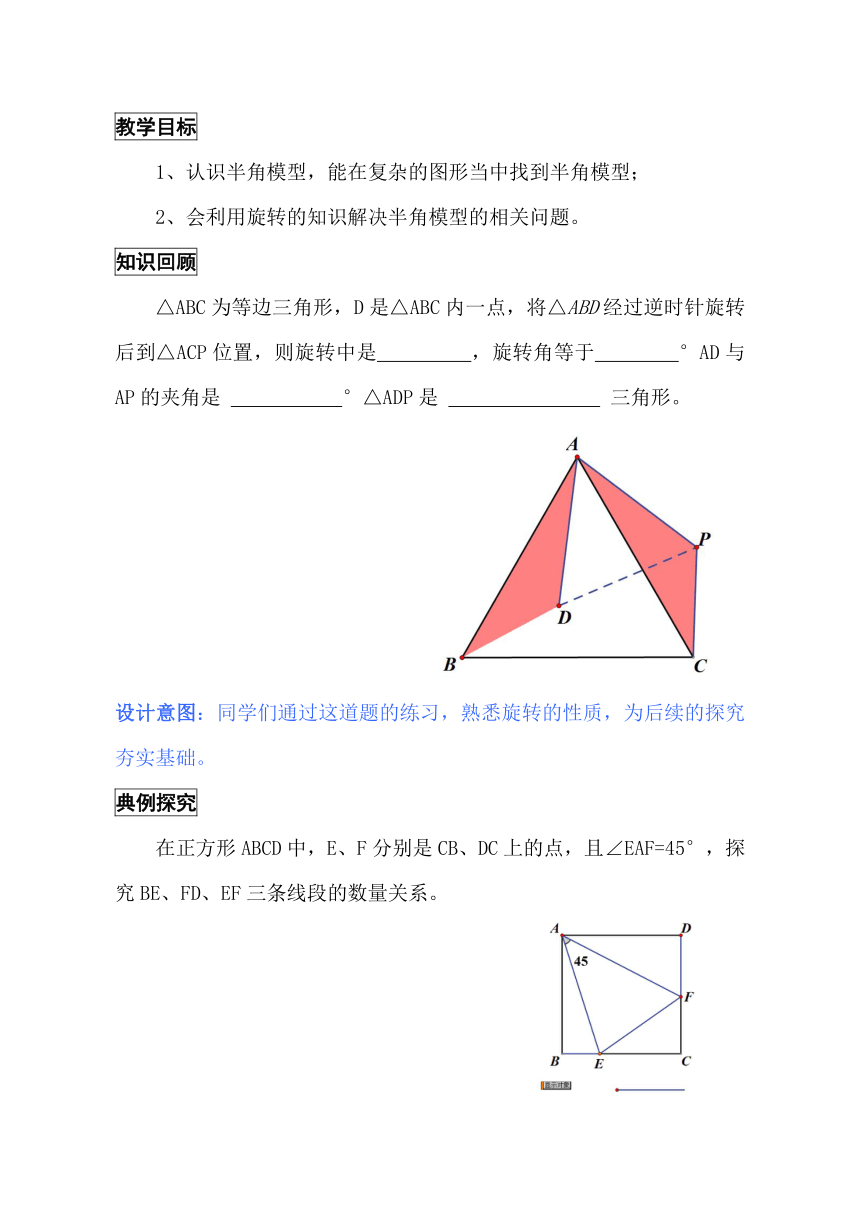
教学目标
1、认识半角模型,能在复杂的图形当中找到半角模型;
2、会利用旋转的知识解决半角模型的相关问题。
知识回顾
△ABC为等边三角形,D是△ABC内一点,将△ABD经过逆时针旋转后到△ACP位置,则旋转中是 ,旋转角等于 °AD与AP的夹角是 °△ADP是 三角形。
设计意图:同学们通过这道题的练习,熟悉旋转的性质,为后续的探究夯实基础。
典例探究
在正方形ABCD中,E、F分别是CB、DC上的点,且∠EAF=45°,探究BE、FD、EF三条线段的数量关系。
(1) 大胆猜测,独立思考,找出解决问题的方法。
(2) 小组讨论,各抒己见,让思维撞击出火花。
(3) 集体讨论,质疑问难,探讨解决问题的方案。
(4) 几何画板演示旋转的意义所在,教师语言要注意引导半角模型的特点。
设计意图:教育本质是一棵树摇动另一棵树,一朵云推动另一朵云,一个灵魂唤醒另一个灵魂。通过个人探究、小组讨论和集体讨论,激发学生对问题的深入思考。几何画板的动态演示直观的展示了旋转的过程中,变与不变的量,变与不变的关系,加深学生对利用旋转解半角模型题目的认知。
变式探究
1、在四边形ABCD中,BA=AD,∠CBA=∠ADC=90°,E、F分别是CB、DC上的点,且∠EAF=∠BAD,BE、FE、DF三条线段之间的数量关系是否仍然成立?
2、在四变形ABCD中,AB=AD,∠EBA+∠ADC=180°,E、F分别是BC、DC上的点,∠EAF=∠BAD,BE、DF、FE三条线段的数量关系是否仍然成立?
(1) 读题的时候,老师就要提醒同学,注意总结和上一道题相比较这道题的已知条件发生了什么样的变化,又有什么不变之处。
(2) 基于上一道题的经验,会有很多同学通过旋转找到答案,可以请一位同学到黑板上展示思路与做法。老师借此了解同学们的思考深度与广度。
(3) 老师适度点拨,启发同学抓住问题的本质。
设计意图:《数学课程标准》指出:“数学教学应从学生已有的知识经验出发,让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型,并对此进行解释和应用。” 通过这三个问题引领学生经历“基本图形——变化的图形——总结归纳解题思路和方法”这样的探究过程,引领学生回顾反思前面的解题经验,找到新的问题的思路和方法,从而达成目标1。
总结提炼
“半角模型”的特征:
1、共端点的 2、共顶点的 。
利用旋转变换解决问题:
1、旋转的目的: ;
2、旋转的条件: ;
3、旋转的方法: 。
先独立思考,然后交流总结出半角模型的标志性特点:共端点的等线段,共顶点的倍半角。旋转的目的是:将分散的条件集中,隐藏的关系显现;旋转的条件是 :相等的线段;旋转的方法是:以公共的端点为旋转中心,以两条相等的线段的夹角为旋转角。
设计意图:让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型的过程。由特殊到一般,建立模型,让学生通过小组合作,自主探索,交流展示等活动,在具体问题的解决过程中体会图形改变,分析解决问题的思路和方法不变,从而达成目标2、3。
拓展延伸
等腰Rt△ABC中,∠DAE=45°,问BD、DE、EC三条线段之间的关系。
要求:在导学案上完成,先独立思考,然后在小组内交流。
设计意图:用这道题题作为前面探究题目的一个提升,目的一是让学生巩固前面所学到的知识,二是激发学生积极主动挑战的热情,为后面的学习积聚动力。
学以致用
在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏西70°的B处,两舰艇到指挥中心距离相等,接到指令后,舰艇甲向正东方向以60节的速度前进,舰艇乙沿北偏东50°方向以80节的速度前进,1.5小时后分别到达E、F处,两舰艇的夹角为70°,求E、F间的距离。
要求:独立完成,统计对错,下课之后收齐,老师批阅
设计意图:这道小测题紧密联系实际,容易引发学生的思考。通过这道题,让学生自我检测,便于查漏补缺。同时,把这节课的掌握情况反馈给老师,让教师心中有数,下节课有的放矢。
总结提升
通过本节课的学习,你有哪些收获?
大家各抒己见。提醒同学从知识和探究方法两方面去谈。
老师送给同学一段话:先有直觉感知,后有逻辑推理。
直觉指明方向,逻辑完善过程。
设计意图:给学生一个反思的机会,教师引导学生对本节课从内容上和学习方法上去进行归纳总结,使学生对本节课的知识进行及时的巩固,条理化,清晰化。通过总结与反思教会学生整理知识的能力,形成系统的知识体系,养成良好的学习习惯和思考和表达的能力。
课后拓展
正方形ABCD中,E、F分别是CB、CD延长线上的点,且∠EAF=45°,探索线段BE、DF与EF的数量关系。
设计意图:这道题与前面的探究题貌似相同实则迥异,通过这节课的学习,学生应该能够感知答案,但是必须深入思考,灵活运用本节课的知识方能破解。数学是思维的体操,希望学生思维更高更强更快!
【教学目标】
结合数学课程标准和学科德育一体化要求,围绕“目标—--评价—--教学”一致性原则,确定本课教学目标如下:
1.明确半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
2.在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
3. 通过讨论交流、合作探究等活动,积累数学活动经验,培养数学学科的严谨思维和理性精神。
【教学重点】
明确半角模型的特点,掌握用旋转的方法解决半角问题的一般思路和方法。
【教学难点】
在解决问题的过程中体会旋转的作用,归纳总结解决半角模型问题的基本方法。
【教学过程】
情境引入
之前,我们学习过图形的变换主要有哪些形式 平移、旋转和轴对称。其中旋转式我们解决几何问题的一大利器。今天我们就来探究如何利用旋转来解决半角模型问题(板书课题)。
教学目标
1、认识半角模型,能在复杂的图形当中找到半角模型;
2、会利用旋转的知识解决半角模型的相关问题。
知识回顾
△ABC为等边三角形,D是△ABC内一点,将△ABD经过逆时针旋转后到△ACP位置,则旋转中是 ,旋转角等于 °AD与AP的夹角是 °△ADP是 三角形。
设计意图:同学们通过这道题的练习,熟悉旋转的性质,为后续的探究夯实基础。
典例探究
在正方形ABCD中,E、F分别是CB、DC上的点,且∠EAF=45°,探究BE、FD、EF三条线段的数量关系。
(1) 大胆猜测,独立思考,找出解决问题的方法。
(2) 小组讨论,各抒己见,让思维撞击出火花。
(3) 集体讨论,质疑问难,探讨解决问题的方案。
(4) 几何画板演示旋转的意义所在,教师语言要注意引导半角模型的特点。
设计意图:教育本质是一棵树摇动另一棵树,一朵云推动另一朵云,一个灵魂唤醒另一个灵魂。通过个人探究、小组讨论和集体讨论,激发学生对问题的深入思考。几何画板的动态演示直观的展示了旋转的过程中,变与不变的量,变与不变的关系,加深学生对利用旋转解半角模型题目的认知。
变式探究
1、在四边形ABCD中,BA=AD,∠CBA=∠ADC=90°,E、F分别是CB、DC上的点,且∠EAF=∠BAD,BE、FE、DF三条线段之间的数量关系是否仍然成立?
2、在四变形ABCD中,AB=AD,∠EBA+∠ADC=180°,E、F分别是BC、DC上的点,∠EAF=∠BAD,BE、DF、FE三条线段的数量关系是否仍然成立?
(1) 读题的时候,老师就要提醒同学,注意总结和上一道题相比较这道题的已知条件发生了什么样的变化,又有什么不变之处。
(2) 基于上一道题的经验,会有很多同学通过旋转找到答案,可以请一位同学到黑板上展示思路与做法。老师借此了解同学们的思考深度与广度。
(3) 老师适度点拨,启发同学抓住问题的本质。
设计意图:《数学课程标准》指出:“数学教学应从学生已有的知识经验出发,让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型,并对此进行解释和应用。” 通过这三个问题引领学生经历“基本图形——变化的图形——总结归纳解题思路和方法”这样的探究过程,引领学生回顾反思前面的解题经验,找到新的问题的思路和方法,从而达成目标1。
总结提炼
“半角模型”的特征:
1、共端点的 2、共顶点的 。
利用旋转变换解决问题:
1、旋转的目的: ;
2、旋转的条件: ;
3、旋转的方法: 。
先独立思考,然后交流总结出半角模型的标志性特点:共端点的等线段,共顶点的倍半角。旋转的目的是:将分散的条件集中,隐藏的关系显现;旋转的条件是 :相等的线段;旋转的方法是:以公共的端点为旋转中心,以两条相等的线段的夹角为旋转角。
设计意图:让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型的过程。由特殊到一般,建立模型,让学生通过小组合作,自主探索,交流展示等活动,在具体问题的解决过程中体会图形改变,分析解决问题的思路和方法不变,从而达成目标2、3。
拓展延伸
等腰Rt△ABC中,∠DAE=45°,问BD、DE、EC三条线段之间的关系。
要求:在导学案上完成,先独立思考,然后在小组内交流。
设计意图:用这道题题作为前面探究题目的一个提升,目的一是让学生巩固前面所学到的知识,二是激发学生积极主动挑战的热情,为后面的学习积聚动力。
学以致用
在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏西70°的B处,两舰艇到指挥中心距离相等,接到指令后,舰艇甲向正东方向以60节的速度前进,舰艇乙沿北偏东50°方向以80节的速度前进,1.5小时后分别到达E、F处,两舰艇的夹角为70°,求E、F间的距离。
要求:独立完成,统计对错,下课之后收齐,老师批阅
设计意图:这道小测题紧密联系实际,容易引发学生的思考。通过这道题,让学生自我检测,便于查漏补缺。同时,把这节课的掌握情况反馈给老师,让教师心中有数,下节课有的放矢。
总结提升
通过本节课的学习,你有哪些收获?
大家各抒己见。提醒同学从知识和探究方法两方面去谈。
老师送给同学一段话:先有直觉感知,后有逻辑推理。
直觉指明方向,逻辑完善过程。
设计意图:给学生一个反思的机会,教师引导学生对本节课从内容上和学习方法上去进行归纳总结,使学生对本节课的知识进行及时的巩固,条理化,清晰化。通过总结与反思教会学生整理知识的能力,形成系统的知识体系,养成良好的学习习惯和思考和表达的能力。
课后拓展
正方形ABCD中,E、F分别是CB、CD延长线上的点,且∠EAF=45°,探索线段BE、DF与EF的数量关系。
设计意图:这道题与前面的探究题貌似相同实则迥异,通过这节课的学习,学生应该能够感知答案,但是必须深入思考,灵活运用本节课的知识方能破解。数学是思维的体操,希望学生思维更高更强更快!
