利用勾股定理求解几何体的最值问题[上学期]
文档属性
| 名称 | 利用勾股定理求解几何体的最值问题[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 75.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-01-06 15:54:00 | ||
图片预览




文档简介
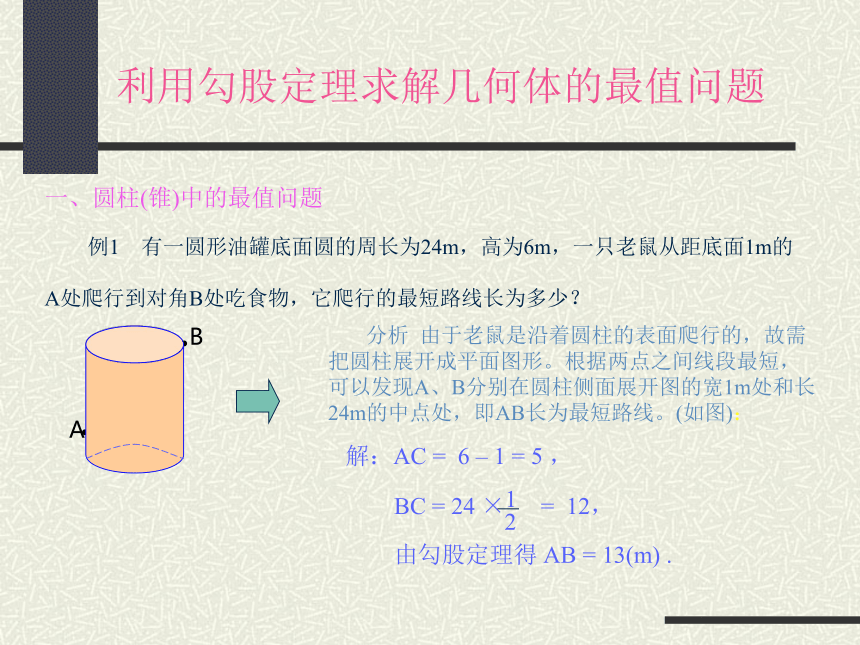
课件13张PPT。利用勾股定理求解几何体的最值问题利用勾股定理求解几何体的最值问题利用勾股定理求解几何体的最值问题 探求最值是初中数学中的一种常见题型,而用勾股定理求立体图形中的最值, 是近年来中考的热点问题之一,对这类问题,我们应该学会分析、观察图形,从中找出解题途径。今天我们来学习用勾股定理解决几何体的最值问题。利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例1 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的
A处爬行到对角B处吃食物,它爬行的最短路线长为多少?利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例1 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的
A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 分析 由于老鼠是沿着圆柱的表面爬行的,故需
把圆柱展开成平面图形。根据两点之间线段最短,
可以发现A、B分别在圆柱侧面展开图的宽1m处和长
24m的中点处,即AB长为最短路线。(如图):利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例1 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的
A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB 分析 由于老鼠是沿着圆柱的表面爬行的,故需
把圆柱展开成平面图形。根据两点之间线段最短,
可以发现A、B分别在圆柱侧面展开图的宽1m处和长
24m的中点处,即AB长为最短路线。(如图):利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例2 壁虎在一座底面半径为2m,高为4m的油罐下底边沿A处发现它的正上方油罐边沿的B处有一只害虫,便决定捕捉它,为了不引起害虫的注意,它故意不走直线,而是绕关油罐,沿一条螺旋路线,从背后对害虫进行突袭,结果偷袭成功,壁虎获得了一顿美餐,请问壁虎至少要爬行多少路线才能捕到害虫? 分析 由于壁虎是沿着油罐表面爬行,并是沿一
条螺旋路线,从背后突袭,我们可以发现壁虎所走
路线是以圆柱侧面展开图为矩形的对角线长。
利用勾股定理求解几何体的最值问题 分析 由于蚂蚁是沿正方体的外表面爬行的,故需
把正方体展开成平面图形(如图所示)。:利用勾股定理求解几何体的最值问题二、长方体、正方体中的最值问题 例4 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=4,CC1=5,一只小虫同A处出发沿长方体表面爬行到C1,这时小虫爬行的最短路长的长度是( ) 解:根据长方体的对称性,小虫爬行的较短路
径有下面三种情况:利用勾股定理求解几何体的最值问题巩 固 练 习 1. 如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点
C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少? 分析 根据题意分析蚂蚁爬行的路线有三种情况(如
图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.:利用勾股定理求解几何体的最值问题巩 固 练 习 2. 如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少? 分析 根据题意分析蚂蚁爬行的路线有两种情况(如
图①② ),由勾股定理可求得图1中AB最短.:利用勾股定理求解几何体的最值问题巩 固 练 习 分析 根据题意和图形,显然蚂蚁先爬长方形A1B1BA; 再爬长 方形ABCD触到琴弦,把长方形ABCD竖起来; 于是就得到A1B1CD. 根据点到直线“垂线段最短”,过点M作MN┷ BE,垂足为N.连结MB、ME,则:N? ? 所以蚂蚁至少需爬行68cm才能触到琴弦。利用勾股定理求解几何体的最值问题小 结:
把几何体适当展开成平面图形,再利用“两点之间线
段最短”,或点到直线“垂线段最短”等性质来解决问题。
A处爬行到对角B处吃食物,它爬行的最短路线长为多少?利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例1 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的
A处爬行到对角B处吃食物,它爬行的最短路线长为多少? 分析 由于老鼠是沿着圆柱的表面爬行的,故需
把圆柱展开成平面图形。根据两点之间线段最短,
可以发现A、B分别在圆柱侧面展开图的宽1m处和长
24m的中点处,即AB长为最短路线。(如图):利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例1 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的
A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB 分析 由于老鼠是沿着圆柱的表面爬行的,故需
把圆柱展开成平面图形。根据两点之间线段最短,
可以发现A、B分别在圆柱侧面展开图的宽1m处和长
24m的中点处,即AB长为最短路线。(如图):利用勾股定理求解几何体的最值问题一、圆柱(锥)中的最值问题 例2 壁虎在一座底面半径为2m,高为4m的油罐下底边沿A处发现它的正上方油罐边沿的B处有一只害虫,便决定捕捉它,为了不引起害虫的注意,它故意不走直线,而是绕关油罐,沿一条螺旋路线,从背后对害虫进行突袭,结果偷袭成功,壁虎获得了一顿美餐,请问壁虎至少要爬行多少路线才能捕到害虫? 分析 由于壁虎是沿着油罐表面爬行,并是沿一
条螺旋路线,从背后突袭,我们可以发现壁虎所走
路线是以圆柱侧面展开图为矩形的对角线长。
利用勾股定理求解几何体的最值问题 分析 由于蚂蚁是沿正方体的外表面爬行的,故需
把正方体展开成平面图形(如图所示)。:利用勾股定理求解几何体的最值问题二、长方体、正方体中的最值问题 例4 如图,长方体ABCD-A1B1C1D1中,AB=3,BC=4,CC1=5,一只小虫同A处出发沿长方体表面爬行到C1,这时小虫爬行的最短路长的长度是( ) 解:根据长方体的对称性,小虫爬行的较短路
径有下面三种情况:利用勾股定理求解几何体的最值问题巩 固 练 习 1. 如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点
C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少? 分析 根据题意分析蚂蚁爬行的路线有三种情况(如
图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.:利用勾股定理求解几何体的最值问题巩 固 练 习 2. 如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少? 分析 根据题意分析蚂蚁爬行的路线有两种情况(如
图①② ),由勾股定理可求得图1中AB最短.:利用勾股定理求解几何体的最值问题巩 固 练 习 分析 根据题意和图形,显然蚂蚁先爬长方形A1B1BA; 再爬长 方形ABCD触到琴弦,把长方形ABCD竖起来; 于是就得到A1B1CD. 根据点到直线“垂线段最短”,过点M作MN┷ BE,垂足为N.连结MB、ME,则:N? ? 所以蚂蚁至少需爬行68cm才能触到琴弦。利用勾股定理求解几何体的最值问题小 结:
把几何体适当展开成平面图形,再利用“两点之间线
段最短”,或点到直线“垂线段最短”等性质来解决问题。
