人教版数学七年级上册3.1.1 一元一次方程公开课课件(共14张PPT)
文档属性
| 名称 | 人教版数学七年级上册3.1.1 一元一次方程公开课课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 35.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-30 22:18:27 | ||
图片预览






文档简介
(共14张PPT)
3.1 从算式到方程
第1课时 一元一次方程
第三章 一元一次方程
1、了解一元一次方程及相关概念,会识
别一元一次方程。
学 习 目 标
2、能找出实际问题中的相等关系,并能列出一元一次方程,体会方程思想.
一、情境导入
问题:一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h,卡车的速度是60km/h,客车比卡车早1h经过B地。A,B两地间的路程是多少?
你能用算术方法解决这个问题吗?
还有其他方法吗?
探究点(一):一元一次方程的概念
二、探究新知
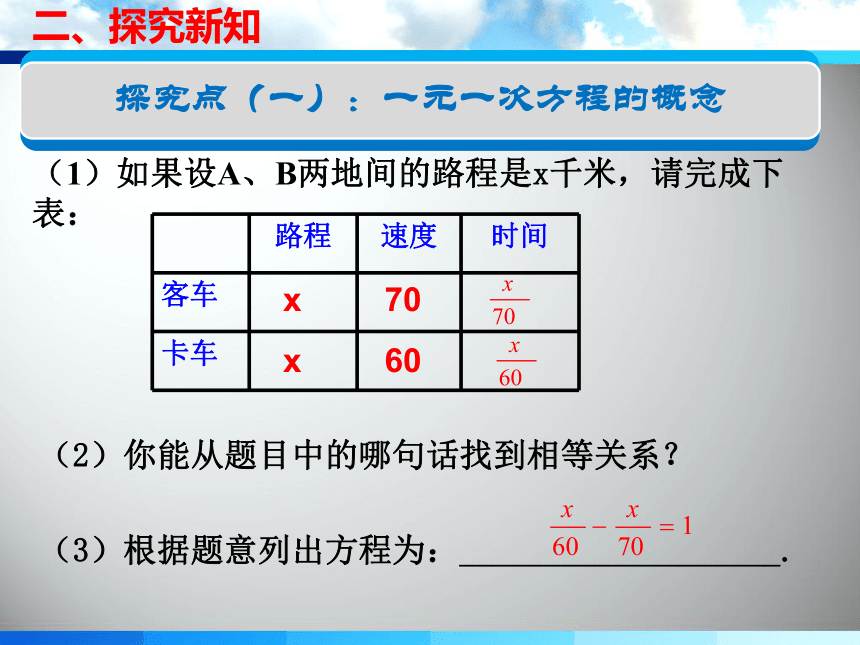
(1)如果设A、B两地间的路程是x千米,请完成下表:
路程 速度 时间
客车
卡车
(2)你能从题目中的哪句话找到相等关系?
(3)根据题意列出方程为:___________________.
x
70
x
60
对于上面的问题,你还能列出其他方程吗?如果能,你依据的是哪个相等关系?
想一想列方程的过程?
设字母表示未知数
找出问题中的等量关系
写出含有未知数的等式
方程
思考
二、探究新知
探究点(二):实际问题中的列方程
例1:根据下列问题,设未知数并列方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x cm,列方程得:
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机使用时间达到规定的检修时间2450小时?
解:设x月后这台计算机的使用时间达到2450小时,那么在x月里这台计算机使用了150x小时.
列方程
4x=24
(3)某校女学生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x,那么女生数为0.52x,男生数为(1-0.52)x.
列方程
探究点(二):实际问题中的列方程
只含有一个未知数(元)x,未知数x的次数是1(次),这样的方程叫做一元一次方程
观察上述所得方程:
二、探究新知
一元一次方程的本质特征:
①含一个未知数(一元);
②未知数次数是1,系数不为0(一次);
③是整式方程(分母中不含未知数)。
实际问题
一元一次方程
设未知数
列方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,使用数学解决实际问题的一种方法.
数学的转化思想
探究点(三):方程的解,解方程
你能猜想出1700+150x=2450的解吗?
怎样验证你的结论?
X=5
x=5时,方程的左边=2450,右边=2450.
此时,左边=右边
所以,x=5是原方程的解。
思考:X=1000和X=2000中哪一个是方程0.52x-(1-0.52)x=80的解?
能使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
名词
动词
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
方程
一元一次方程方程的解
解方程
四个概念
一元一次方程
三、课堂小结
一种方法
一个数学思想
列方程解决实际问题的方法
转化
四、巩固练习
1.下列条件中,能列出一元一次方程的是:( )
A.x与-2的差的一半; B.一个数的2倍是3
C.x与y的和是27的50%; D.甲数的3倍与乙数的和
2.x=3是下列哪个方程的解 ( )
A. 2x+6=0 B.4x=10-x C.5(x-3)=0 D.2x-7=12
3.若2x+1与x-4互为相反数,则可得方程:
________________________.
4.某数χ的相反数比它的2倍大1,求某数。 列方程
为:____________.
5. 有一棵树,刚移栽时,树高为2m,假设以后平均每
年长0.3m,几年后树高为5m?
解:设x年后树高为5m,可列出方程 ___
B
C
2x+1+(x-4)=0
-x-2x=1
2+0.3x=5
3.1 从算式到方程
第1课时 一元一次方程
第三章 一元一次方程
1、了解一元一次方程及相关概念,会识
别一元一次方程。
学 习 目 标
2、能找出实际问题中的相等关系,并能列出一元一次方程,体会方程思想.
一、情境导入
问题:一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h,卡车的速度是60km/h,客车比卡车早1h经过B地。A,B两地间的路程是多少?
你能用算术方法解决这个问题吗?
还有其他方法吗?
探究点(一):一元一次方程的概念
二、探究新知
(1)如果设A、B两地间的路程是x千米,请完成下表:
路程 速度 时间
客车
卡车
(2)你能从题目中的哪句话找到相等关系?
(3)根据题意列出方程为:___________________.
x
70
x
60
对于上面的问题,你还能列出其他方程吗?如果能,你依据的是哪个相等关系?
想一想列方程的过程?
设字母表示未知数
找出问题中的等量关系
写出含有未知数的等式
方程
思考
二、探究新知
探究点(二):实际问题中的列方程
例1:根据下列问题,设未知数并列方程:
(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少?
解:设正方形的边长为x cm,列方程得:
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机使用时间达到规定的检修时间2450小时?
解:设x月后这台计算机的使用时间达到2450小时,那么在x月里这台计算机使用了150x小时.
列方程
4x=24
(3)某校女学生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校的学生数为x,那么女生数为0.52x,男生数为(1-0.52)x.
列方程
探究点(二):实际问题中的列方程
只含有一个未知数(元)x,未知数x的次数是1(次),这样的方程叫做一元一次方程
观察上述所得方程:
二、探究新知
一元一次方程的本质特征:
①含一个未知数(一元);
②未知数次数是1,系数不为0(一次);
③是整式方程(分母中不含未知数)。
实际问题
一元一次方程
设未知数
列方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,使用数学解决实际问题的一种方法.
数学的转化思想
探究点(三):方程的解,解方程
你能猜想出1700+150x=2450的解吗?
怎样验证你的结论?
X=5
x=5时,方程的左边=2450,右边=2450.
此时,左边=右边
所以,x=5是原方程的解。
思考:X=1000和X=2000中哪一个是方程0.52x-(1-0.52)x=80的解?
能使方程左右两边相等的未知数的值叫做方程的解。
求方程的解的过程叫做解方程。
名词
动词
检验一个数是不是方程的解的步骤:
1.将数值代入方程左边进行计算,
2.将数值代入方程右边进行计算,
3.比较左右两边的值,若左边=右边,则是方程的解,反之,则不是.
方程
一元一次方程方程的解
解方程
四个概念
一元一次方程
三、课堂小结
一种方法
一个数学思想
列方程解决实际问题的方法
转化
四、巩固练习
1.下列条件中,能列出一元一次方程的是:( )
A.x与-2的差的一半; B.一个数的2倍是3
C.x与y的和是27的50%; D.甲数的3倍与乙数的和
2.x=3是下列哪个方程的解 ( )
A. 2x+6=0 B.4x=10-x C.5(x-3)=0 D.2x-7=12
3.若2x+1与x-4互为相反数,则可得方程:
________________________.
4.某数χ的相反数比它的2倍大1,求某数。 列方程
为:____________.
5. 有一棵树,刚移栽时,树高为2m,假设以后平均每
年长0.3m,几年后树高为5m?
解:设x年后树高为5m,可列出方程 ___
B
C
2x+1+(x-4)=0
-x-2x=1
2+0.3x=5
