人教版 七年级上册一元一次方程 优质课件(共18张PPT)
文档属性
| 名称 | 人教版 七年级上册一元一次方程 优质课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 669.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
3.1 从算式到方程(第1课时) 3.1.1 一元一次方程
义务教育教科书 数学 七年级 上册
名人语录
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡尔Descartes
一、温故知新--了解方程的概念
微课自学:课前已通过微课自学方式下发到班级微信群中,
微课内容:自学第三章章节引言了解3个问题
1.方程的定义 2.列方程研究问题的步骤
3.本章主要研究内容
学案检测:
1.下列各式是方程的是 。
②③④⑤⑧
问题1:一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地. A,B两地间的路程是多少?
二、学习新知—体会算式到方程是数学的一大进步
(1)算术方法解温馨提示:
对于 1km 的路程,客车行驶的时间是 h,
卡车行驶的时间是 h ,
客车比卡车少用的时间是 h ,
路程是多少千米时,客车比卡车少用的时间是1 h ?
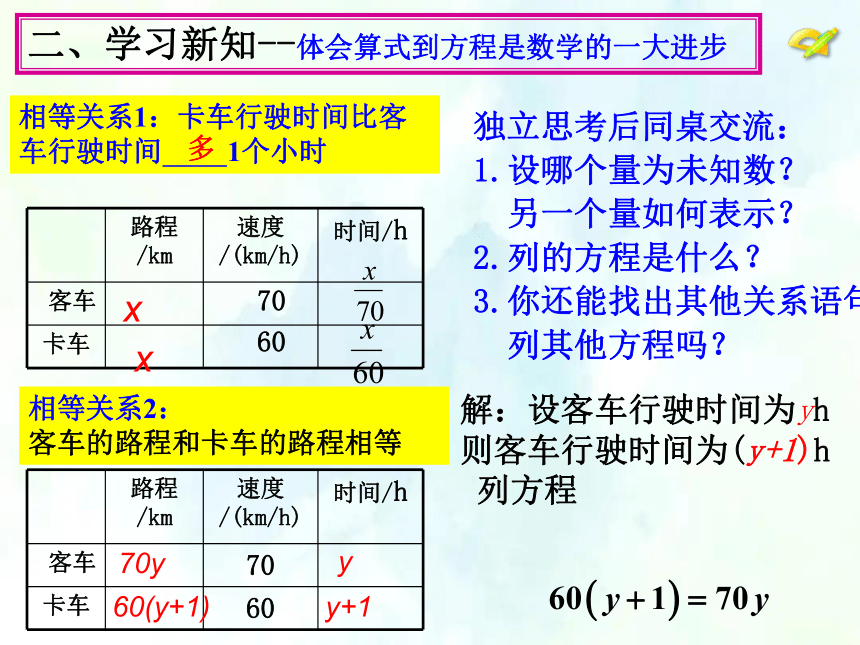
二、学习新知--体会算式到方程是数学的一大进步
路程/km 速度/(km/h) 时间/h
客车
卡车
路程/km 速度/(km/h) 时间/h
客车 70
卡车 60
x
y
x
y+1
70y
60(y+1)
独立思考后同桌交流:
1.设哪个量为未知数?
另一个量如何表示?
2.列的方程是什么?
3.你还能找出其他关系语句
列其他方程吗?
相等关系1:卡车行驶时间比客车行驶时间 1个小时
相等关系2:
客车的路程和卡车的路程相等
多
解:设客车行驶时间为yh
则客车行驶时间为(y+1)h
列方程
70
60
(1)用一根长24 cm的铁丝围成一个正方形,正 方形的边长是多少?
解:设正方形的边长为x cm.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
问题2: 根据下面问题,设未知数列出方程,
并思考:列方程依据的相等关系是什么?
相等关系:4×边长=正方形的周长
(2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定
的检修时间2450 h?
解: 设x月后这台计算机的使用时间达到2450 h,
那么在x月里这台计算机使用了150x h.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
问题2:
相等关系1:已使用时间+预计使用时间=规定检修时间
相等关系2:预计使用时间=规定检修时间-已使用时间
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校有x名同学,那么有0.52x名女生,
(1-0.52)x名男生.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
相等关系1:女生人数-男生人数=80
相等关系2:女生人数=男生人数+80
相等关系3:女生人数+男生人数=全校人数
问题2:
三、巩固训练--了解一元一次方程的概念
题组二
1.下列各式是方程的是 。
②③④⑤⑧
2.1题中是一元一次方程的是 。
②③
题组二
2.根据下列问题,设未知数,列出方程:
(1)环形跑道一周长400m ,沿跑道跑多少周可以跑3000m
(2)甲种铅笔每支0.3元,乙种铅笔每支0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?
(3)用买10个大水杯的钱,可以买15个小水杯,大水杯比小水杯的单价多5元,两种水杯的单价各是多少元?
400x=3000
0.3x+0.6(20-x)=9
15x=10(x+5)
三、巩固训练--体会方程的思想
解:沿跑道跑x周可以跑3000m,
解:设买了甲种铅笔x只,那么买了乙种铅笔(20-x)只,
解:设小水杯的单价x元,那么设大水杯的单价(x+5)元,
实际问题
设未知数
找相等关系
列方程
列出方程后,还要求出符合方程的未知数的值.
二、学习新知--感受方程刻画现实世界的数学模型的意义
2.思考:x=1 000和x=2 000中哪一个是方程
的解?
当x=1 000时,左边= ,
当x=2 000时,
所以,x=1 000不是方程的解.
所以,x=2 000是方程的解.
二、学习新知--了解解方程及方程的解的概念
问题3:阅读课本P80完成下列问题(自主学习)
左边40≠ 右边80
左边=
左边80=右边80
三、巩固训练--了解解方程及方程的解的概念
题组三:
4.判断题.(对的打“∨”,错的“×”)
(1)x=2是方程x-10=-4x解. ( )
(2)x=1或x=-1都是方程x2-1=0的解.( )
∨”
∨”
左边=-8,
右边=-8,
左边-8=右边-8
当x=1时,左边=1-1=0,
右边=0,
左边=右边
当x=-1时,左边=1-1=0,
右边=0,
左边=右边
四、拓展延伸--升华一元一次方程的概念
1. +21=0是一元一次方程,则k=__;
2. +21=0是一元一次方程,则k=____;
2
-1
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
五、课堂小结--归纳总结思想升华
作业:
(1)基础作业:教科书习题3.1第2、3、7、8题.
(2)提高作业:教科书习题3.1第11题.
五、作业—巩固提升
(1)本节课学习了哪些主要内容?
(2)一元一次方程的三个特征各指什么?
(3)从实际问题中列出方程的关键是什么?
五、课堂小结--归纳总结思想升华
作业:
(1)基础作业:教科书习题3.1第2、3、7、8题.
(2)提高作业:教科书习题3.1第11题.
全品71页
A组:6题——13题
B组:1题——11题
C组:1题——7题
六:布置作业
3.1 从算式到方程(第1课时) 3.1.1 一元一次方程
义务教育教科书 数学 七年级 上册
名人语录
“一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程问题,因此,一旦解决了方程问题,一切问题将迎刃而解!”
——法国数学家 笛卡尔Descartes
一、温故知新--了解方程的概念
微课自学:课前已通过微课自学方式下发到班级微信群中,
微课内容:自学第三章章节引言了解3个问题
1.方程的定义 2.列方程研究问题的步骤
3.本章主要研究内容
学案检测:
1.下列各式是方程的是 。
②③④⑤⑧
问题1:一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70 km/h,卡车的行驶速度是60 km/h,客车比卡车早1 h经过B地. A,B两地间的路程是多少?
二、学习新知—体会算式到方程是数学的一大进步
(1)算术方法解温馨提示:
对于 1km 的路程,客车行驶的时间是 h,
卡车行驶的时间是 h ,
客车比卡车少用的时间是 h ,
路程是多少千米时,客车比卡车少用的时间是1 h ?
二、学习新知--体会算式到方程是数学的一大进步
路程/km 速度/(km/h) 时间/h
客车
卡车
路程/km 速度/(km/h) 时间/h
客车 70
卡车 60
x
y
x
y+1
70y
60(y+1)
独立思考后同桌交流:
1.设哪个量为未知数?
另一个量如何表示?
2.列的方程是什么?
3.你还能找出其他关系语句
列其他方程吗?
相等关系1:卡车行驶时间比客车行驶时间 1个小时
相等关系2:
客车的路程和卡车的路程相等
多
解:设客车行驶时间为yh
则客车行驶时间为(y+1)h
列方程
70
60
(1)用一根长24 cm的铁丝围成一个正方形,正 方形的边长是多少?
解:设正方形的边长为x cm.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
问题2: 根据下面问题,设未知数列出方程,
并思考:列方程依据的相等关系是什么?
相等关系:4×边长=正方形的周长
(2)一台计算机已使用1700 h,预计每月再使用150 h,经过多少月这台计算机的使用时间达到规定
的检修时间2450 h?
解: 设x月后这台计算机的使用时间达到2450 h,
那么在x月里这台计算机使用了150x h.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
问题2:
相等关系1:已使用时间+预计使用时间=规定检修时间
相等关系2:预计使用时间=规定检修时间-已使用时间
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
解:设这个学校有x名同学,那么有0.52x名女生,
(1-0.52)x名男生.
列方程 .
二、学习新知--感受方程刻画现实世界的数学模型的意义
相等关系1:女生人数-男生人数=80
相等关系2:女生人数=男生人数+80
相等关系3:女生人数+男生人数=全校人数
问题2:
三、巩固训练--了解一元一次方程的概念
题组二
1.下列各式是方程的是 。
②③④⑤⑧
2.1题中是一元一次方程的是 。
②③
题组二
2.根据下列问题,设未知数,列出方程:
(1)环形跑道一周长400m ,沿跑道跑多少周可以跑3000m
(2)甲种铅笔每支0.3元,乙种铅笔每支0.6元,用9元钱买了两种铅笔共20支,两种铅笔各买了多少支?
(3)用买10个大水杯的钱,可以买15个小水杯,大水杯比小水杯的单价多5元,两种水杯的单价各是多少元?
400x=3000
0.3x+0.6(20-x)=9
15x=10(x+5)
三、巩固训练--体会方程的思想
解:沿跑道跑x周可以跑3000m,
解:设买了甲种铅笔x只,那么买了乙种铅笔(20-x)只,
解:设小水杯的单价x元,那么设大水杯的单价(x+5)元,
实际问题
设未知数
找相等关系
列方程
列出方程后,还要求出符合方程的未知数的值.
二、学习新知--感受方程刻画现实世界的数学模型的意义
2.思考:x=1 000和x=2 000中哪一个是方程
的解?
当x=1 000时,左边= ,
当x=2 000时,
所以,x=1 000不是方程的解.
所以,x=2 000是方程的解.
二、学习新知--了解解方程及方程的解的概念
问题3:阅读课本P80完成下列问题(自主学习)
左边40≠ 右边80
左边=
左边80=右边80
三、巩固训练--了解解方程及方程的解的概念
题组三:
4.判断题.(对的打“∨”,错的“×”)
(1)x=2是方程x-10=-4x解. ( )
(2)x=1或x=-1都是方程x2-1=0的解.( )
∨”
∨”
左边=-8,
右边=-8,
左边-8=右边-8
当x=1时,左边=1-1=0,
右边=0,
左边=右边
当x=-1时,左边=1-1=0,
右边=0,
左边=右边
四、拓展延伸--升华一元一次方程的概念
1. +21=0是一元一次方程,则k=__;
2. +21=0是一元一次方程,则k=____;
2
-1
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
畅所欲言
五、课堂小结--归纳总结思想升华
作业:
(1)基础作业:教科书习题3.1第2、3、7、8题.
(2)提高作业:教科书习题3.1第11题.
五、作业—巩固提升
(1)本节课学习了哪些主要内容?
(2)一元一次方程的三个特征各指什么?
(3)从实际问题中列出方程的关键是什么?
五、课堂小结--归纳总结思想升华
作业:
(1)基础作业:教科书习题3.1第2、3、7、8题.
(2)提高作业:教科书习题3.1第11题.
全品71页
A组:6题——13题
B组:1题——11题
C组:1题——7题
六:布置作业
