人教版 七年级上册 用等式的性质解方程 公开课课件(共21张PPT)
文档属性
| 名称 | 人教版 七年级上册 用等式的性质解方程 公开课课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 28.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 08:50:28 | ||
图片预览


文档简介
(共21张PPT)
人教版七年级数学(上册)
第三章一元一次方程
3.1.2用等式的性质解方程
(第2课时)
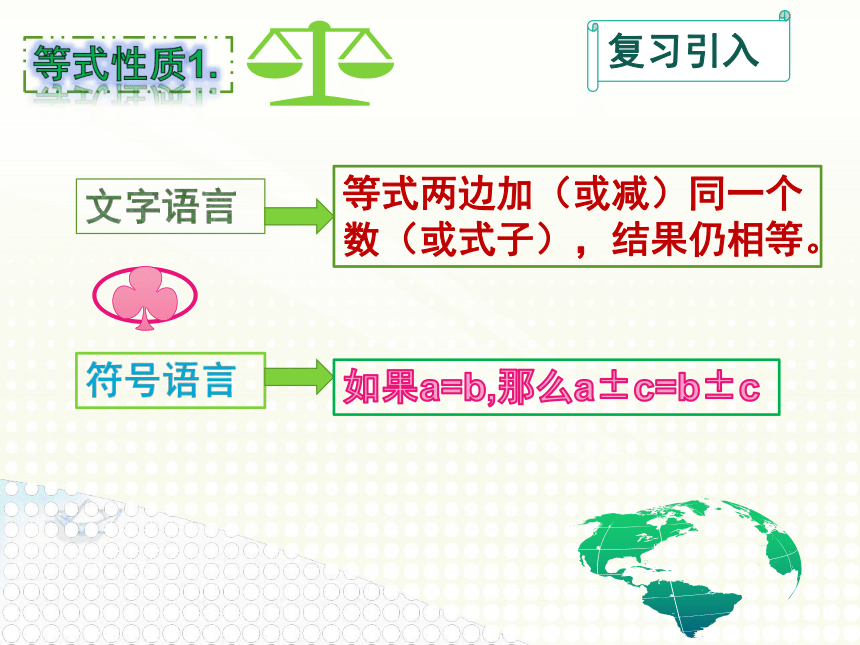
等式两边加(或减)同一个数(或式子),结果仍相等。
等式性质1.
文字语言
符号语言
如果a=b,那么a±c=b±c
复习引入
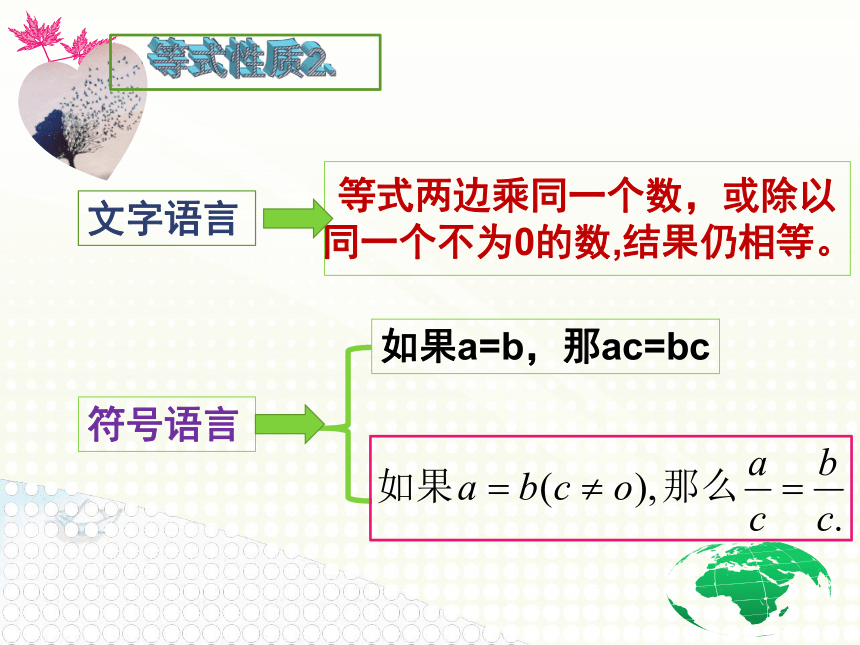
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式性质2.
文字语言
符号语言
如果a=b,那ac=bc
一个等式如果含有未知数就成了方程,如果不含有未知数就不是方程。
方程与等式的关系:
探究
含有未知数的等式叫方程
方程一定是等式
而等式不一定是方程
方程定义
恒等式
条件等式
矛盾等式
研究解的情况?
方程中的等式的3种形式
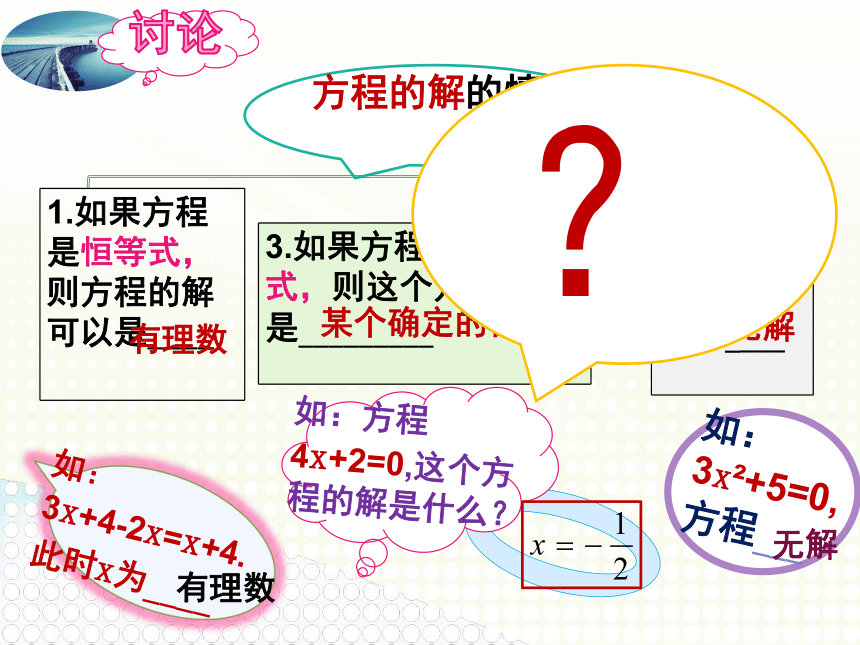
如:
3x+4-2x=x+4.此时x为____
1.如果方程是恒等式,则方程的解可以是____
有理数
3.如果方程是条件等式,则这个方程的解是_________
某个确定的值
2.如果方程是矛盾等式,则方程____
无解
有理数
如:方程4x+2=0,这个方程的解是什么?
讨论
方程的解的情况
如:3x +5=0,方程___
无解
?
这是本节课我们要研究的内容——利用等式的性质解方程——今天我们来学习利用等式的性质
解一元一次方程。
引入新课
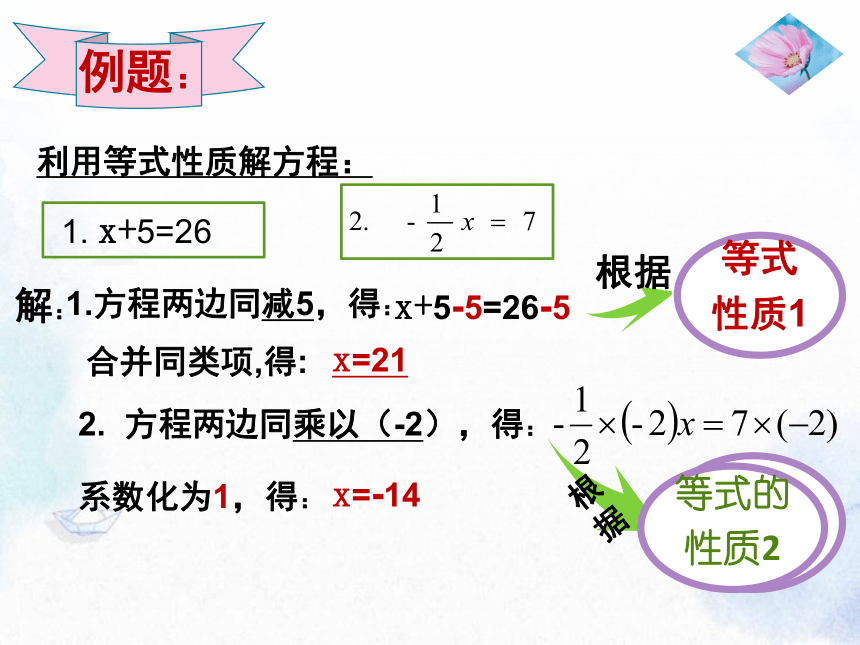
例题:
利用等式性质解方程:
1. x+5=26
1.方程两边同减5,得:
合并同类项,得:
x+5-5=26-5
解:
x=21
2. 方程两边同乘以(-2),得:
系数化为1,得:
x=-14
根据
等式
性质1
等式的性质2
根据
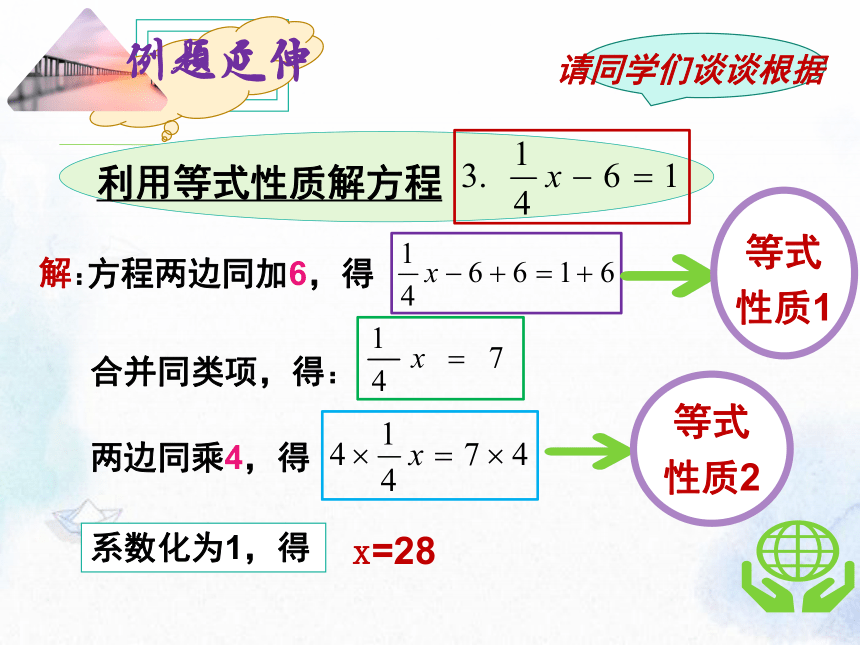
利用等式性质解方程
解:
方程两边同加6,得
合并同类项,得:
两边同乘4,得
系数化为1,得
x=28
请同学们谈谈根据
等式性质1
等式性质2
例题延伸
利用等式性质解方程,并检验:
-3x-1=3
2x+4=5x
请同学演练
孩子们掌握了吗?
变式练习
2.
1.
一元一次方程的几种常见形式及求解方法:
(1)x+a=b,
反思归纳
两边都同减去a,得:
x=b-a;
(2)ax=b(a≠0),
两边同除以a,得:
(3)ax+b=c(a≠o),
两边都同减去b,得:
两边再同除以a,得:
ax=c-b
利用等式的性质解方程的一般
2.利用等式的性质2,方程两边同乘(或除以)同一个数(除数不为0),得到 的形式。
1.利用等式的性质1,方程两边同加(或减)同一个数,把方程变形为ax=b(a≠0)的形式.
步骤
基础训练
1.下列变形中正确的是
①. 由x-6=5得,x=11.
( )
②. 由-5x=10得,x=2.
④.
( )
( )
③.
( )
1.用适当的数或式子填空:
-6
(1). 若3x+6=2x,则 3x=2x______ .
根据 ____________,在方程两边同____.
等式性质1,
-6
18.
根据____________ ,在方程两边同_____.
x9
等式性质2
___
填空训练
训练—选择题
1.下列利用等式的性质解方程中,正确的是( )
A.由x-5=3得,x=-2
D.由4x=-8得,x=-2。
D
2.下列解方程的方法正确的是( )A.f'n'g'fB.LOREM IPSUM DOLOR拓展训练C.D.C.此题展开讲解3.如果代数式5x-7与4x+9的值互为相反数,则x的值为( )D拓展延伸
用等式的性质解方程
等式的性质
1.等式两边加(或减)同一个数(或式子),结果仍相等。
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
形式x=m
1.方程两边同加(或减)同一个数(或式子),得到ax=b(a≠0)的形式
2.方程两边同乘(或除以)同一个数(除数不为0),得到x=m的形式
知识小结
随堂小测试
1.如果0.6x=2-0.4x,那么x=___.
2.
___
(一):填空题
(二)选择题
4.利用等式性质把方程2x+7=22转化为x=a的形式?
(三)解答题
x=2
分数的基本性质
C
a=0时无解
阶梯式课后作业
1.若代数式4x-2的值为6,则x的值为( )
A.2 B.-2 C.1 D.-1
2.若方程3x+k=x-1的解为x=2,求k的值
3.方程2x+1=3和方程2x-a=0的解相同,求a的值
4.依据等式性质,求y的值:
5.教课书第83页,第4题。
谢谢 再见
谢谢 再见
人教版七年级数学(上册)
第三章一元一次方程
3.1.2用等式的性质解方程
(第2课时)
等式两边加(或减)同一个数(或式子),结果仍相等。
等式性质1.
文字语言
符号语言
如果a=b,那么a±c=b±c
复习引入
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式性质2.
文字语言
符号语言
如果a=b,那ac=bc
一个等式如果含有未知数就成了方程,如果不含有未知数就不是方程。
方程与等式的关系:
探究
含有未知数的等式叫方程
方程一定是等式
而等式不一定是方程
方程定义
恒等式
条件等式
矛盾等式
研究解的情况?
方程中的等式的3种形式
如:
3x+4-2x=x+4.此时x为____
1.如果方程是恒等式,则方程的解可以是____
有理数
3.如果方程是条件等式,则这个方程的解是_________
某个确定的值
2.如果方程是矛盾等式,则方程____
无解
有理数
如:方程4x+2=0,这个方程的解是什么?
讨论
方程的解的情况
如:3x +5=0,方程___
无解
?
这是本节课我们要研究的内容——利用等式的性质解方程——今天我们来学习利用等式的性质
解一元一次方程。
引入新课
例题:
利用等式性质解方程:
1. x+5=26
1.方程两边同减5,得:
合并同类项,得:
x+5-5=26-5
解:
x=21
2. 方程两边同乘以(-2),得:
系数化为1,得:
x=-14
根据
等式
性质1
等式的性质2
根据
利用等式性质解方程
解:
方程两边同加6,得
合并同类项,得:
两边同乘4,得
系数化为1,得
x=28
请同学们谈谈根据
等式性质1
等式性质2
例题延伸
利用等式性质解方程,并检验:
-3x-1=3
2x+4=5x
请同学演练
孩子们掌握了吗?
变式练习
2.
1.
一元一次方程的几种常见形式及求解方法:
(1)x+a=b,
反思归纳
两边都同减去a,得:
x=b-a;
(2)ax=b(a≠0),
两边同除以a,得:
(3)ax+b=c(a≠o),
两边都同减去b,得:
两边再同除以a,得:
ax=c-b
利用等式的性质解方程的一般
2.利用等式的性质2,方程两边同乘(或除以)同一个数(除数不为0),得到 的形式。
1.利用等式的性质1,方程两边同加(或减)同一个数,把方程变形为ax=b(a≠0)的形式.
步骤
基础训练
1.下列变形中正确的是
①. 由x-6=5得,x=11.
( )
②. 由-5x=10得,x=2.
④.
( )
( )
③.
( )
1.用适当的数或式子填空:
-6
(1). 若3x+6=2x,则 3x=2x______ .
根据 ____________,在方程两边同____.
等式性质1,
-6
18.
根据____________ ,在方程两边同_____.
x9
等式性质2
___
填空训练
训练—选择题
1.下列利用等式的性质解方程中,正确的是( )
A.由x-5=3得,x=-2
D.由4x=-8得,x=-2。
D
2.下列解方程的方法正确的是( )A.f'n'g'fB.LOREM IPSUM DOLOR拓展训练C.D.C.此题展开讲解3.如果代数式5x-7与4x+9的值互为相反数,则x的值为( )D拓展延伸
用等式的性质解方程
等式的性质
1.等式两边加(或减)同一个数(或式子),结果仍相等。
2.等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
形式x=m
1.方程两边同加(或减)同一个数(或式子),得到ax=b(a≠0)的形式
2.方程两边同乘(或除以)同一个数(除数不为0),得到x=m的形式
知识小结
随堂小测试
1.如果0.6x=2-0.4x,那么x=___.
2.
___
(一):填空题
(二)选择题
4.利用等式性质把方程2x+7=22转化为x=a的形式?
(三)解答题
x=2
分数的基本性质
C
a=0时无解
阶梯式课后作业
1.若代数式4x-2的值为6,则x的值为( )
A.2 B.-2 C.1 D.-1
2.若方程3x+k=x-1的解为x=2,求k的值
3.方程2x+1=3和方程2x-a=0的解相同,求a的值
4.依据等式性质,求y的值:
5.教课书第83页,第4题。
谢谢 再见
谢谢 再见
