人教版七年级上册 3.1.2等式的性质 精品课件(共37张PPT)
文档属性
| 名称 | 人教版七年级上册 3.1.2等式的性质 精品课件(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 08:54:12 | ||
图片预览






文档简介
(共37张PPT)
3.1 从算式到方程
等式的性质
回顾: 什么叫方程?
什么叫方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
上述这组式子中,( )是等式, ( ) 是一元一次方程
① ② 2x ③ 3x+1,
④
ab S= ah,
2x-3y>0
2
3
1
2
①④⑤⑦
①④⑤
判 断
⑦
⑤
⑥
⑧
法国数学家笛卡尔说:“一切问题都可以转化为数学问题;一切数学问题都可以转化为代数问题;一切代数问题都可以转化为方程问题,因此,解决了方程问题,一切问题都将迎刃而解.
3.1 从算式到方程
等式的性质学习目标
1、通过观察、分析得出等式的两条性质
2、会利用等式的两条性质解方程
如果在平衡后的跷跷板的一侧加物品,要想保持跷跷板的平衡,需要怎么做
等式的性质
天平与等式
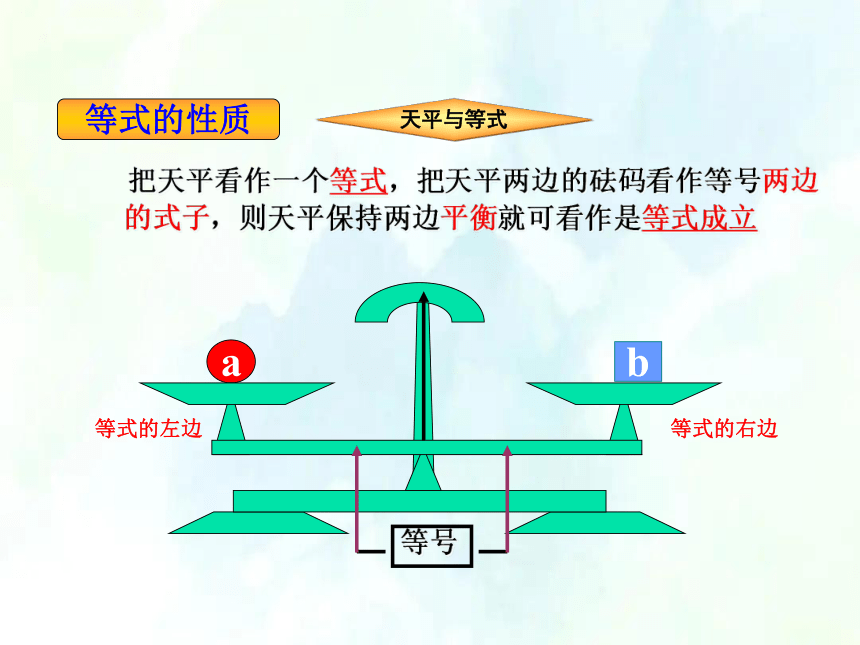
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立
b
a
等式的左边
等式的右边
等号
a
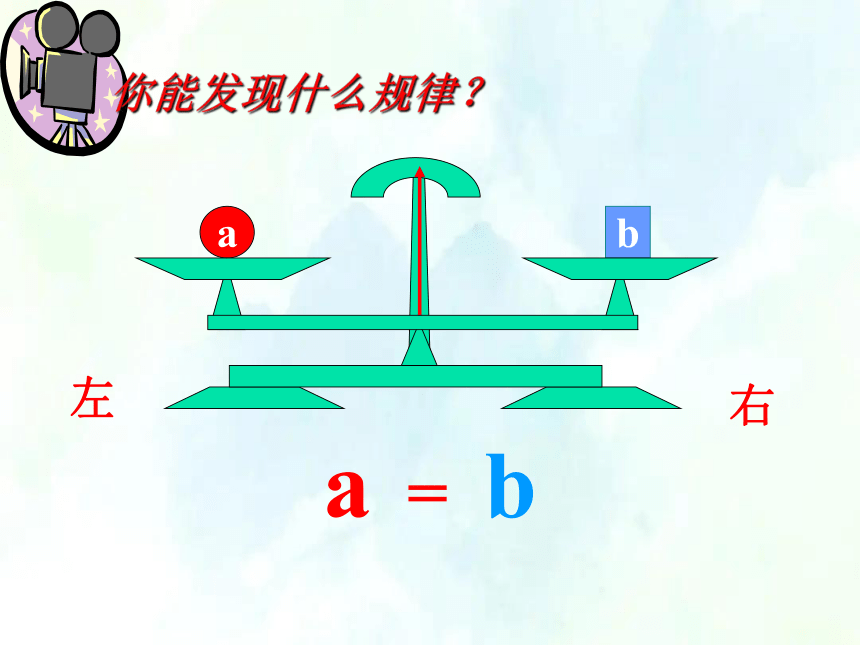
你能发现什么规律?
右
左
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
a = b
右
左
b
a
你能发现什么规律?
a = b
c
右
左
a
c
b
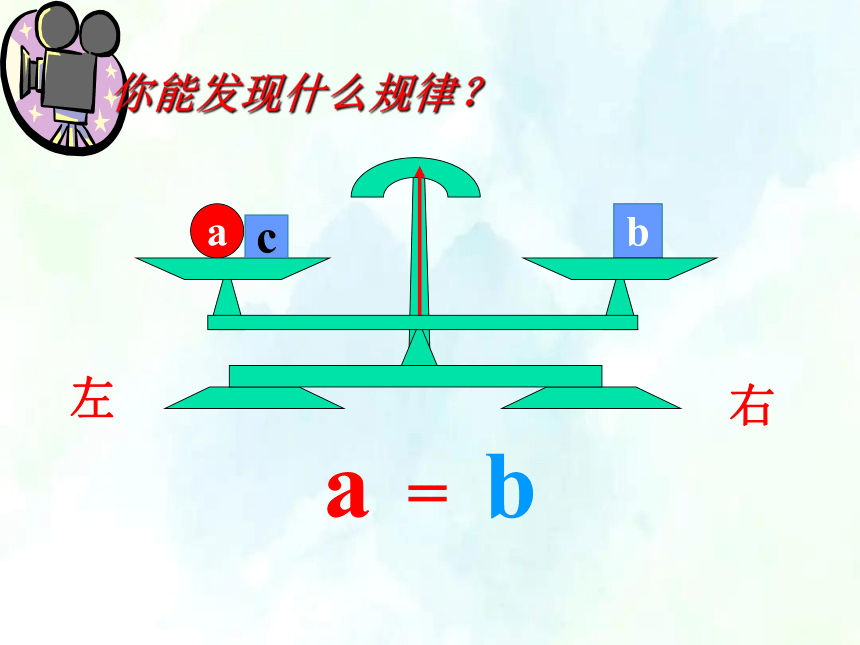
你能发现什么规律?
a = b
右
左
c
b
c
a
你能发现什么规律?
a = b
a+c b+c
=
右
左
c
c
你能发现什么规律?
a = b
b
a
左
c
你能发现什么规律?
a = b
b
a
右
左
你能发现什么规律?
a = b
a
b
右
左
你能发现什么规律?
a = b
a-c b-c
=
a
b
右
左
等式的性质
等式两边加(或减)同一个数(或式子),结果仍相等.
【等式性质 1】
如果a=b,那么a±c=______
b±c
b
a
你能发现什么规律?
a = b
右
左
b
a
你能发现什么规律?
a = b
右
左
a
b
2a = 2b
b
a
你能发现什么规律?
a = b
右
左
b
b
a
a
3a = 3b
b
a
你能发现什么规律?
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
a
b
a
你能发现什么规律?
a = b
右
左
(c≠0)
【等式性质 2】
等式的性质
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
即:如果a=b,那么ac=______
如果a=b(c≠0),那么a/c=______
bc
b/c
等式的性质1:
等式两边加(或减)
同一个数(或式子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0的数,结果
仍相等。
——
等式的两个性质
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
快乐练习
√
+2 +2
① 若 x-2 = 3,根据__________,得到 x-2 = 3 ,转化为 x = 5 。
② 若 -4 x = 3,根据___________,
得到 ,转化为x =____ 。
等式的性质1
等式的性质2
解一元一次方程就是利用等式的性质求出
方程解的过程。化为x=a(常数)的形式
快乐练习
问题:解方程的依据和方程结果的形式是?
解:(1)两边减7,得
(2)两边同时除以-5,得
(3)两边加5,得
化简得:
两边同乘-3,得
用等式的性质解方程
化成X=a的形式
于是
于是
方程的解的检验
3x + 7 = 1 的解是x = -2。对吗
检验: 把 x= -2 代入原方程的两边
左边= 3×(- 2)+7
= 1
右边= 1
左边=右边
所以x= -2是原方程的解
注意:要带入原方程。
(1) 0.3x=15 (2) 5x+4=0
(3) x-4=7 (4) 2x-1=7
(5)2x=6 (6)1-3x=7
快乐练习
下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
x = 0
x = 9
a =
牛刀小试
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。 聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
补偿提高
谈谈收获
这节课我们学到了什么?
小结:
1、等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
2、等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
3、解一元一次方程的实质就是利用等式的
性质求出未知数的值
书面作业:P83习题 3.1的第4题。
家庭作业:习题 3.1其他题。
再见
3.1 从算式到方程
等式的性质
回顾: 什么叫方程?
什么叫方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
上述这组式子中,( )是等式, ( ) 是一元一次方程
① ② 2x ③ 3x+1,
④
ab S= ah,
2x-3y>0
2
3
1
2
①④⑤⑦
①④⑤
判 断
⑦
⑤
⑥
⑧
法国数学家笛卡尔说:“一切问题都可以转化为数学问题;一切数学问题都可以转化为代数问题;一切代数问题都可以转化为方程问题,因此,解决了方程问题,一切问题都将迎刃而解.
3.1 从算式到方程
等式的性质学习目标
1、通过观察、分析得出等式的两条性质
2、会利用等式的两条性质解方程
如果在平衡后的跷跷板的一侧加物品,要想保持跷跷板的平衡,需要怎么做
等式的性质
天平与等式
把天平看作一个等式,把天平两边的砝码看作等号两边的式子,则天平保持两边平衡就可看作是等式成立
b
a
等式的左边
等式的右边
等号
a
你能发现什么规律?
右
左
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
右
左
b
a
你能发现什么规律?
a = b
右
左
b
a
你能发现什么规律?
a = b
c
右
左
a
c
b
你能发现什么规律?
a = b
右
左
c
b
c
a
你能发现什么规律?
a = b
a+c b+c
=
右
左
c
c
你能发现什么规律?
a = b
b
a
左
c
你能发现什么规律?
a = b
b
a
右
左
你能发现什么规律?
a = b
a
b
右
左
你能发现什么规律?
a = b
a-c b-c
=
a
b
右
左
等式的性质
等式两边加(或减)同一个数(或式子),结果仍相等.
【等式性质 1】
如果a=b,那么a±c=______
b±c
b
a
你能发现什么规律?
a = b
右
左
b
a
你能发现什么规律?
a = b
右
左
a
b
2a = 2b
b
a
你能发现什么规律?
a = b
右
左
b
b
a
a
3a = 3b
b
a
你能发现什么规律?
a = b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac = bc
a
b
a
你能发现什么规律?
a = b
右
左
(c≠0)
【等式性质 2】
等式的性质
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
即:如果a=b,那么ac=______
如果a=b(c≠0),那么a/c=______
bc
b/c
等式的性质1:
等式两边加(或减)
同一个数(或式子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0的数,结果
仍相等。
——
等式的两个性质
(1)如果x=y,那么 ( )
(2)如果x=y,那么 ( )
(3)如果x=y,那么 ( )
(4)如果x=y,那么 ( )
(5)如果x=y,那么 ( )
判断对错,对的说明根据等式的哪一条性质;错的说出为什么。
×
√
×
×
快乐练习
√
+2 +2
① 若 x-2 = 3,根据__________,得到 x-2 = 3 ,转化为 x = 5 。
② 若 -4 x = 3,根据___________,
得到 ,转化为x =____ 。
等式的性质1
等式的性质2
解一元一次方程就是利用等式的性质求出
方程解的过程。化为x=a(常数)的形式
快乐练习
问题:解方程的依据和方程结果的形式是?
解:(1)两边减7,得
(2)两边同时除以-5,得
(3)两边加5,得
化简得:
两边同乘-3,得
用等式的性质解方程
化成X=a的形式
于是
于是
方程的解的检验
3x + 7 = 1 的解是x = -2。对吗
检验: 把 x= -2 代入原方程的两边
左边= 3×(- 2)+7
= 1
右边= 1
左边=右边
所以x= -2是原方程的解
注意:要带入原方程。
(1) 0.3x=15 (2) 5x+4=0
(3) x-4=7 (4) 2x-1=7
(5)2x=6 (6)1-3x=7
快乐练习
下列各式的变形正确的是( )
A.由 ,得到 x = 2
B.由 ,得到 x = 1
C.由-2 a = -3,得到 a =
D.由 x-1 = 4,得到 x = 5
D
x = 0
x = 9
a =
牛刀小试
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。 聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
补偿提高
谈谈收获
这节课我们学到了什么?
小结:
1、等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等。
2、等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
如果 a = b,那么 a ± c = b ± c
如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
3、解一元一次方程的实质就是利用等式的
性质求出未知数的值
书面作业:P83习题 3.1的第4题。
家庭作业:习题 3.1其他题。
再见
