人教版七年级上册 3.1.2 等式的性质 优质课件 (共28张PPT)
文档属性
| 名称 | 人教版七年级上册 3.1.2 等式的性质 优质课件 (共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 735.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 08:54:58 | ||
图片预览






文档简介
(共28张PPT)
§3.1.2等式的性质
中国人智商不一般!!
IQ就是智商
140以上 天才或近于天才
120-140 智力优异
110-120 智力较高
90-110 普通智力
中国人拥有全世界最高的平均智商,平均值为110。
难!!!
【猜猜猜!】
估计一下方程的解
等式性质
解方程
方程的解
(化成“x=a”)
体会“化归”的思想
重点
难点
学习目标
1、什么是方程?
2、什么是方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
【温故知新】
m+n = n+m
x+2x = 3x
3×3+1= 5×2
3x+1 = 5y
这4个式子的共同点是什么?
用等号“=”来表示相等关系的式子,叫做等式。a=b
有“=”
是等式
【独具慧眼】
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
2
3
1
2
①④⑥⑦⑨
②③⑤⑧⑩
【明察秋毫】
+
-
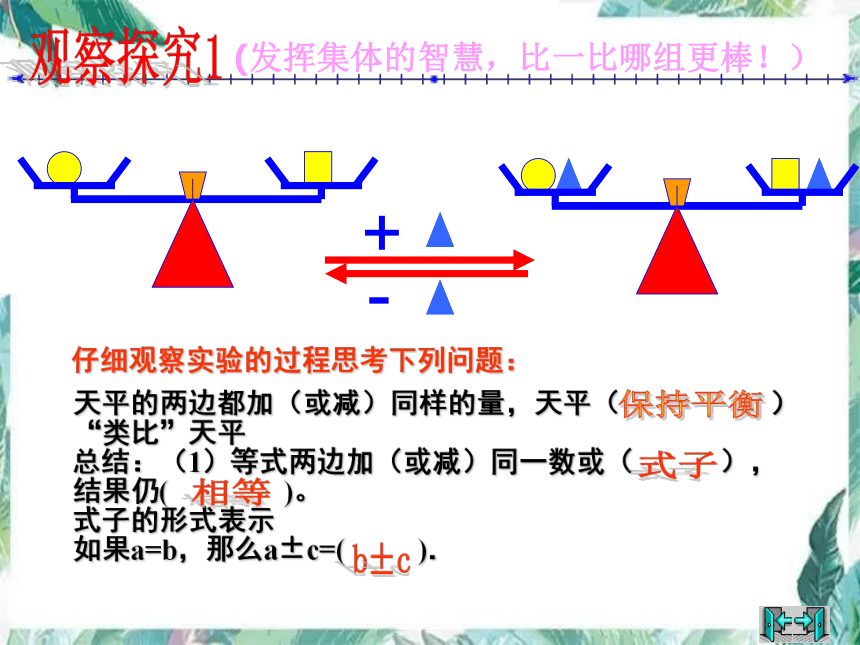
观察探究1
天平的两边都加(或减)同样的量,天平( ) “类比”天平
总结:(1)等式两边加(或减)同一数或( ),
结果仍( )。
式子的形式表示
如果a=b,那么a±c=( ).
仔细观察实验的过程思考下列问题:
保持平衡
式子
b±c
相等
(发挥集体的智慧,比一比哪组更棒!)
×3
÷3
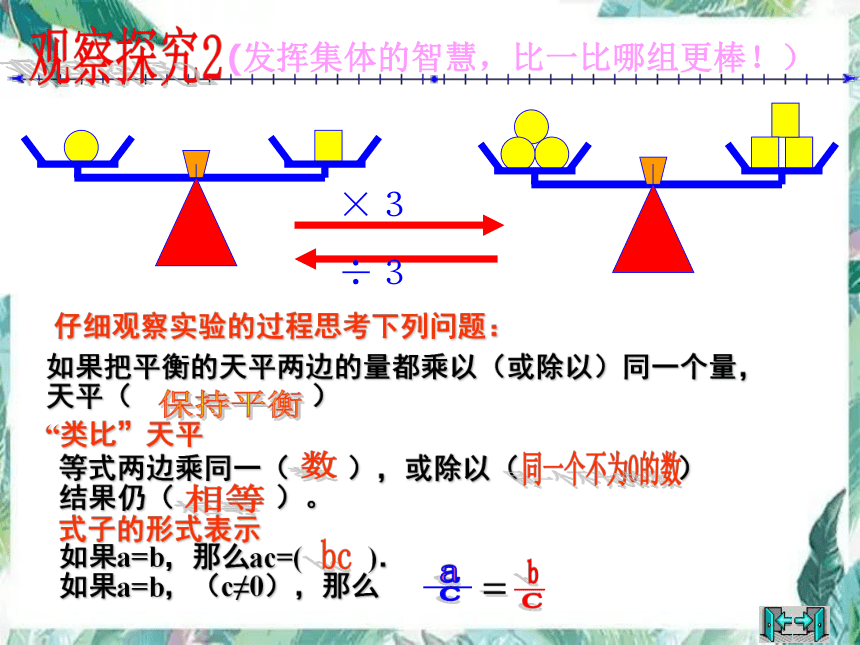
观察探究2
仔细观察实验的过程思考下列问题:
如果把平衡的天平两边的量都乘以(或除以)同一个量,
天平( )
“类比”天平
等式两边乘同一( ),或除以( )
结果仍( )。
如果a=b,那么ac=( ).
如果a=b,(c≠0),那么
a
C
b
C
=
bc
式子的形式表示
数
同一个不为0的数
保持平衡
相等
(发挥集体的智慧,比一比哪组更棒!)
等式的性质1:
等式两边加(或减)
同一个数(或式子子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0数,结果仍
相等。
——
等式的两性质
【归纳总结】
即:如果 ,
那么
即:如果 ,那么
如果 (c≠0) ,那么
例题:利用等式的性质解下列方程:
【初露锋芒】
(2)(3)小组合作完成,展示。
解:
(1)两边减7,得
于是
例 中解下列方程:
解:两边加上5 ,
化简,得
两边同时 ,
乘 -3
得 x =
-27。
得
x=-27是原
方程的解
吗
(等式性质1)
(等式性质2)
【指点迷津】
(如何检验?)
将 代入方程 的左边,得
方程的左右两边相等,所以 是方程的解。
注意:要带入原方程。
【指点迷津】
七(1)班同学们,大家好!
7个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们组将直接过关;否则要考验你们数学问题,如果你们组答不出来,其他组可以回答.每关最高分8分!
快乐之旅
1
2
3
4
5
6
7
(1) 怎样从等式 5x=4x+3 得到等式 x=3
(2) 怎样从等式 4x=12 得到等式 x=3
(1) 怎样从等式 得到等式 a=b
(2) 怎样从等式 2πR=2πr 得到等式R=r
用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = ( 50 )
根据等式性质 2,等式两边都除以 0.2 或乘以 5。
+2 +2
=
(1) 若 x-2 = 3,根据____________ ,
得到 x-2 = 3 ,即 x = 5 。
(2) 若 -4 x = 3,根据___________ ,
得到 ,即x =____ 。
等式的性质1
等式的性质2
(1) 从 a+2=b+2 能不能得到 a=b ?为什么?
(2) 从-3a=-3b 能不能得到 a=b ?为什么?
任写一个以x=1为解的一元一次方程 。
恭喜你,过关了!
本节课你学会了什么
对大家说,
你有什么收获?
对老师说,
你还有什么困惑?
等式的性质
1: 等式两边加(或减)同一个数
(或式子),结果仍相等。
如果 a = b
那么 a + c = b + c
2: 等式两边乘同一个数或 除以
同一个不为0的数,结果仍相等。
如果 a = b 那么 ac = bc
如果 a = b 那么
a b
c c
__ __
=
(c≠0)
掌握关键:<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
解方程的目标: 变形 x = a (常数)
检验的方法
(代 入)
原方程
收获的季节
填空:(每空5分)
①如果x-3=2,那么x-3+3= _____ ,
根据
②如果4x=-12y,那么x= ,
2、 利用等式性质,解下列方程。
(1) x-5=6
(2)5x+4 = 0
x =11
4
5
-
=
x
2+3
等式性质1,在等式两边同加3
根据
-3y
等式性质2,在等式两边同时除以4
独立完成,同桌交换阅卷,组内订正。
(每题10分)
【自我检测】
领先一步
【布置作业】
【必做】P84-85 3、4
【选作】 P84-85 7、8、9
你们太棒了!谢谢合作
拓展探索
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
§3.1.2等式的性质
中国人智商不一般!!
IQ就是智商
140以上 天才或近于天才
120-140 智力优异
110-120 智力较高
90-110 普通智力
中国人拥有全世界最高的平均智商,平均值为110。
难!!!
【猜猜猜!】
估计一下方程的解
等式性质
解方程
方程的解
(化成“x=a”)
体会“化归”的思想
重点
难点
学习目标
1、什么是方程?
2、什么是方程的解?
含有未知数的等式——方程
使方程中等号左右两边相等的未知数的值——方程的解
【温故知新】
m+n = n+m
x+2x = 3x
3×3+1= 5×2
3x+1 = 5y
这4个式子的共同点是什么?
用等号“=”来表示相等关系的式子,叫做等式。a=b
有“=”
是等式
【独具慧眼】
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y>0
2
3
1
2
①④⑥⑦⑨
②③⑤⑧⑩
【明察秋毫】
+
-
观察探究1
天平的两边都加(或减)同样的量,天平( ) “类比”天平
总结:(1)等式两边加(或减)同一数或( ),
结果仍( )。
式子的形式表示
如果a=b,那么a±c=( ).
仔细观察实验的过程思考下列问题:
保持平衡
式子
b±c
相等
(发挥集体的智慧,比一比哪组更棒!)
×3
÷3
观察探究2
仔细观察实验的过程思考下列问题:
如果把平衡的天平两边的量都乘以(或除以)同一个量,
天平( )
“类比”天平
等式两边乘同一( ),或除以( )
结果仍( )。
如果a=b,那么ac=( ).
如果a=b,(c≠0),那么
a
C
b
C
=
bc
式子的形式表示
数
同一个不为0的数
保持平衡
相等
(发挥集体的智慧,比一比哪组更棒!)
等式的性质1:
等式两边加(或减)
同一个数(或式子子),结果仍相等。
等式的性质2:
等式两边乘同一
个数,或除以同一
个不为0数,结果仍
相等。
——
等式的两性质
【归纳总结】
即:如果 ,
那么
即:如果 ,那么
如果 (c≠0) ,那么
例题:利用等式的性质解下列方程:
【初露锋芒】
(2)(3)小组合作完成,展示。
解:
(1)两边减7,得
于是
例 中解下列方程:
解:两边加上5 ,
化简,得
两边同时 ,
乘 -3
得 x =
-27。
得
x=-27是原
方程的解
吗
(等式性质1)
(等式性质2)
【指点迷津】
(如何检验?)
将 代入方程 的左边,得
方程的左右两边相等,所以 是方程的解。
注意:要带入原方程。
【指点迷津】
七(1)班同学们,大家好!
7个金蛋你可以任选一个,如果出现“恭喜你”的字样,你们组将直接过关;否则要考验你们数学问题,如果你们组答不出来,其他组可以回答.每关最高分8分!
快乐之旅
1
2
3
4
5
6
7
(1) 怎样从等式 5x=4x+3 得到等式 x=3
(2) 怎样从等式 4x=12 得到等式 x=3
(1) 怎样从等式 得到等式 a=b
(2) 怎样从等式 2πR=2πr 得到等式R=r
用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = ( 50 )
根据等式性质 2,等式两边都除以 0.2 或乘以 5。
+2 +2
=
(1) 若 x-2 = 3,根据____________ ,
得到 x-2 = 3 ,即 x = 5 。
(2) 若 -4 x = 3,根据___________ ,
得到 ,即x =____ 。
等式的性质1
等式的性质2
(1) 从 a+2=b+2 能不能得到 a=b ?为什么?
(2) 从-3a=-3b 能不能得到 a=b ?为什么?
任写一个以x=1为解的一元一次方程 。
恭喜你,过关了!
本节课你学会了什么
对大家说,
你有什么收获?
对老师说,
你还有什么困惑?
等式的性质
1: 等式两边加(或减)同一个数
(或式子),结果仍相等。
如果 a = b
那么 a + c = b + c
2: 等式两边乘同一个数或 除以
同一个不为0的数,结果仍相等。
如果 a = b 那么 ac = bc
如果 a = b 那么
a b
c c
__ __
=
(c≠0)
掌握关键:<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
解方程的目标: 变形 x = a (常数)
检验的方法
(代 入)
原方程
收获的季节
填空:(每空5分)
①如果x-3=2,那么x-3+3= _____ ,
根据
②如果4x=-12y,那么x= ,
2、 利用等式性质,解下列方程。
(1) x-5=6
(2)5x+4 = 0
x =11
4
5
-
=
x
2+3
等式性质1,在等式两边同加3
根据
-3y
等式性质2,在等式两边同时除以4
独立完成,同桌交换阅卷,组内订正。
(每题10分)
【自我检测】
领先一步
【布置作业】
【必做】P84-85 3、4
【选作】 P84-85 7、8、9
你们太棒了!谢谢合作
拓展探索
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
