人教版七年级上册3.1.2等式的性质 优质课件(共20张PPT)
文档属性
| 名称 | 人教版七年级上册3.1.2等式的性质 优质课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 882.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
3.1.2 等式的性质
人教版七年级(上)
回顾与思考:
只含有一个未知数(元),未知
数的次数都是1,等号两边都是整式的方程叫一元一次方程。
一元一次方程:
请叙述一元一次方程的概念?
你能用估算的方法求下列方程的解吗?
很简单,就是
X=
X=a(a为常数)
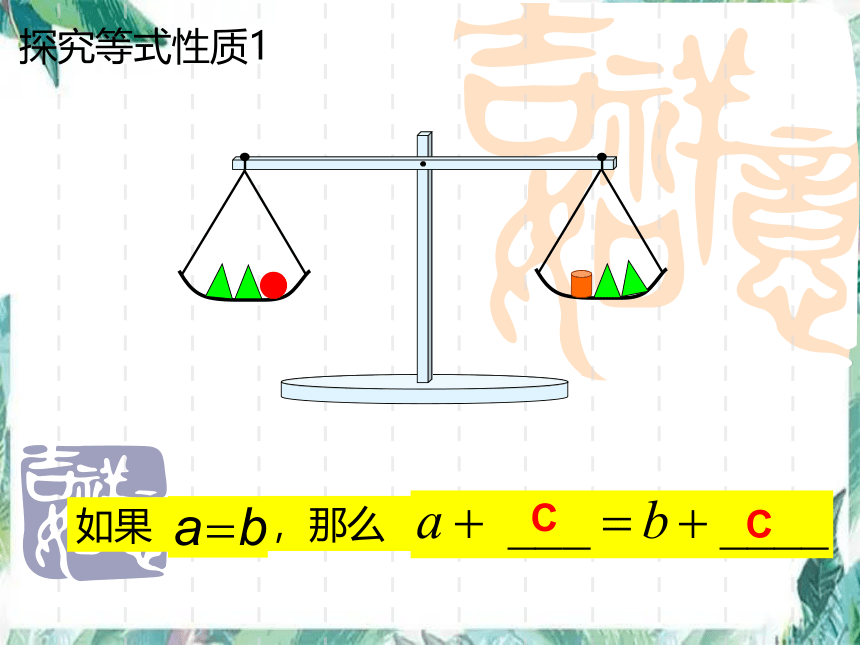
探究等式性质1
C
C
a=b
a
b
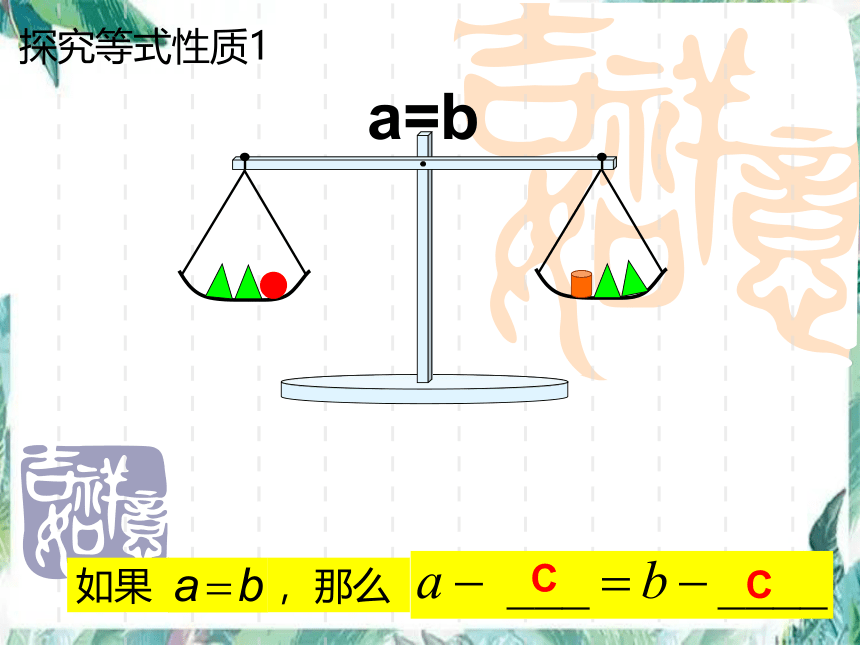
探究等式性质1
,那么
如果
C
C
探究等式性质1
,那么
如果
C
C
a=b
探究等式性质1
,那么
如果
等式两边加(或减)同一个数(或式子),结果
仍相等。
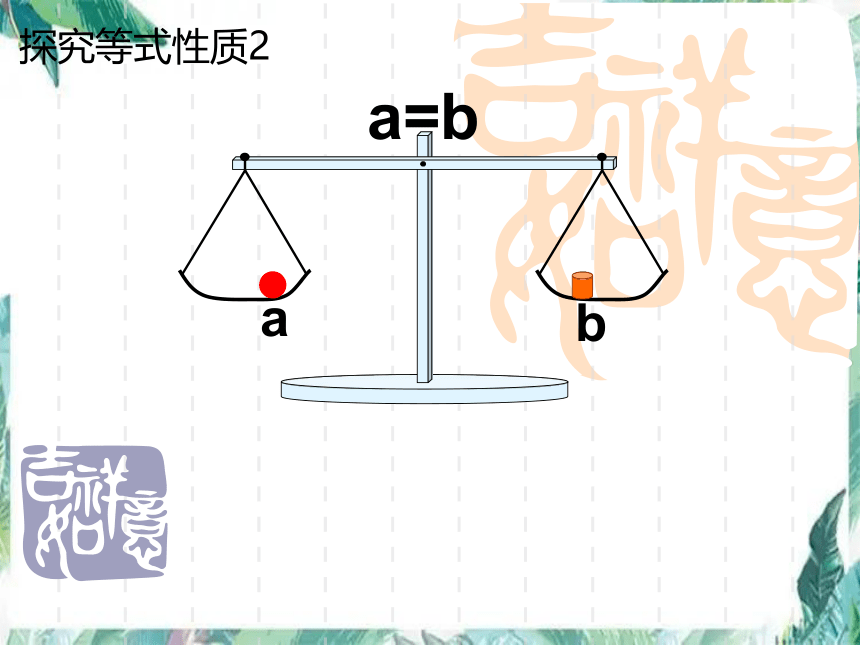
探究等式性质2
a=b
a
b
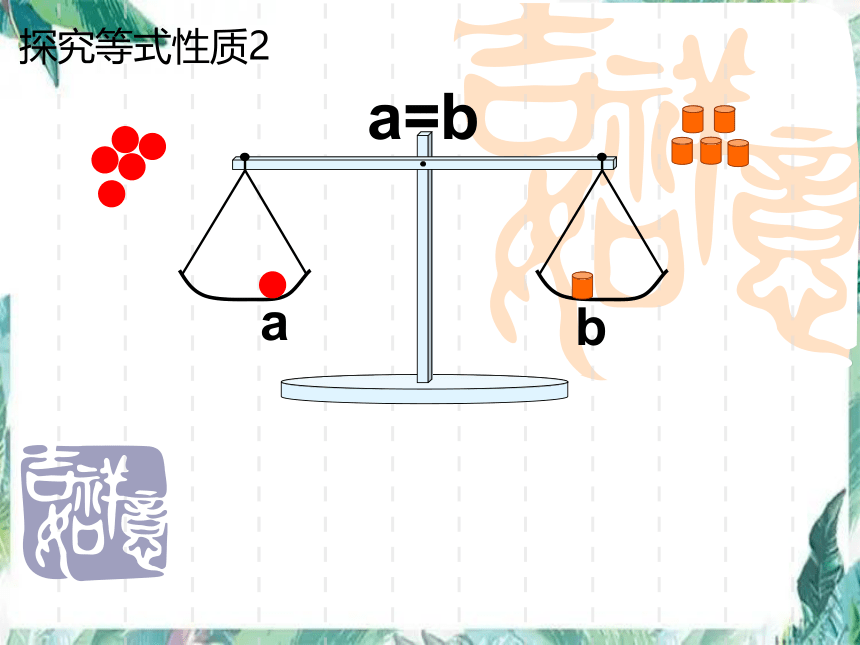
探究等式性质2
a=b
a
b
探究等式性质2
,那么
如果
×6 ×6
×7 ×7
×9 ×9
探究等式性质2
a=b
,那么
如果
6 6
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等。
,那么
如果
,那么
如果
等式两边都乘(或除以)同一个数(除数不能是0),所得的等式仍然成立。
等式两边都加上(或减去)同一个数或整式,所得的等式仍然成立。
如果
, 那么
如果 , 那么
等式的基本性质
等式的性质1:
等式的性质2:
如果 , 那么
课本
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 ,那么 ( )
练一练:判断对错,对的请说出根据等式的哪 一条性质,错的请说出为什么。
√
×
×
×
√
√
√
×
例2:利用等式的性质解下列方程
解:两边减7,得
于是
解:两边除以-5,得
于是
X=a(a为常数)
例2:利用等式的性质解下列方程
解:两边加5,得
化简,得
两边同乘-3,得
检验:
将
代入方程
,得:
左边
右边
所以
是方程
的解。
利用等式的性质解下列方程:
练习
小结:
学习完本课之后你有什么收获?
1、等式的性质有几条?
用字母怎样表示?
2、解方程最终必须将方程
化作什么形式?
等式两边都乘(或除以)同一个数(除数不能是0),所得的等式仍然成立。
等式两边都加上(或减去)同一个数或整式,所得的等式仍然成立。
如果
, 那么
如果 , 那么
等式的基本性质
等式的性质1:
等式的性质2:
如果 , 那么
课本
欢迎各位老师莅临指导
谢谢
3.1.2 等式的性质
人教版七年级(上)
回顾与思考:
只含有一个未知数(元),未知
数的次数都是1,等号两边都是整式的方程叫一元一次方程。
一元一次方程:
请叙述一元一次方程的概念?
你能用估算的方法求下列方程的解吗?
很简单,就是
X=
X=a(a为常数)
探究等式性质1
C
C
a=b
a
b
探究等式性质1
,那么
如果
C
C
探究等式性质1
,那么
如果
C
C
a=b
探究等式性质1
,那么
如果
等式两边加(或减)同一个数(或式子),结果
仍相等。
探究等式性质2
a=b
a
b
探究等式性质2
a=b
a
b
探究等式性质2
,那么
如果
×6 ×6
×7 ×7
×9 ×9
探究等式性质2
a=b
,那么
如果
6 6
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等。
,那么
如果
,那么
如果
等式两边都乘(或除以)同一个数(除数不能是0),所得的等式仍然成立。
等式两边都加上(或减去)同一个数或整式,所得的等式仍然成立。
如果
, 那么
如果 , 那么
等式的基本性质
等式的性质1:
等式的性质2:
如果 , 那么
课本
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 , 那么 ( )
如果 ,那么 ( )
练一练:判断对错,对的请说出根据等式的哪 一条性质,错的请说出为什么。
√
×
×
×
√
√
√
×
例2:利用等式的性质解下列方程
解:两边减7,得
于是
解:两边除以-5,得
于是
X=a(a为常数)
例2:利用等式的性质解下列方程
解:两边加5,得
化简,得
两边同乘-3,得
检验:
将
代入方程
,得:
左边
右边
所以
是方程
的解。
利用等式的性质解下列方程:
练习
小结:
学习完本课之后你有什么收获?
1、等式的性质有几条?
用字母怎样表示?
2、解方程最终必须将方程
化作什么形式?
等式两边都乘(或除以)同一个数(除数不能是0),所得的等式仍然成立。
等式两边都加上(或减去)同一个数或整式,所得的等式仍然成立。
如果
, 那么
如果 , 那么
等式的基本性质
等式的性质1:
等式的性质2:
如果 , 那么
课本
欢迎各位老师莅临指导
谢谢
