北师大版八年级数学上册试题 一课一练1.3勾股定理的应用--勾股定理与翻折问题(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 一课一练1.3勾股定理的应用--勾股定理与翻折问题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 132.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 10:07:52 | ||
图片预览


文档简介
1.3勾股定理的应用--勾股定理与翻折问题
一、选择题
1.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为( )
A.6 B.8 C.12 D.14
2.如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,AB=6,则△EBF周长的大小为( )
A.8 B.10 C.12 D.6
3.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A.3 B.4 C.5 D.6
4.如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
A.3.6 B.4 C.4.8 D.6.4
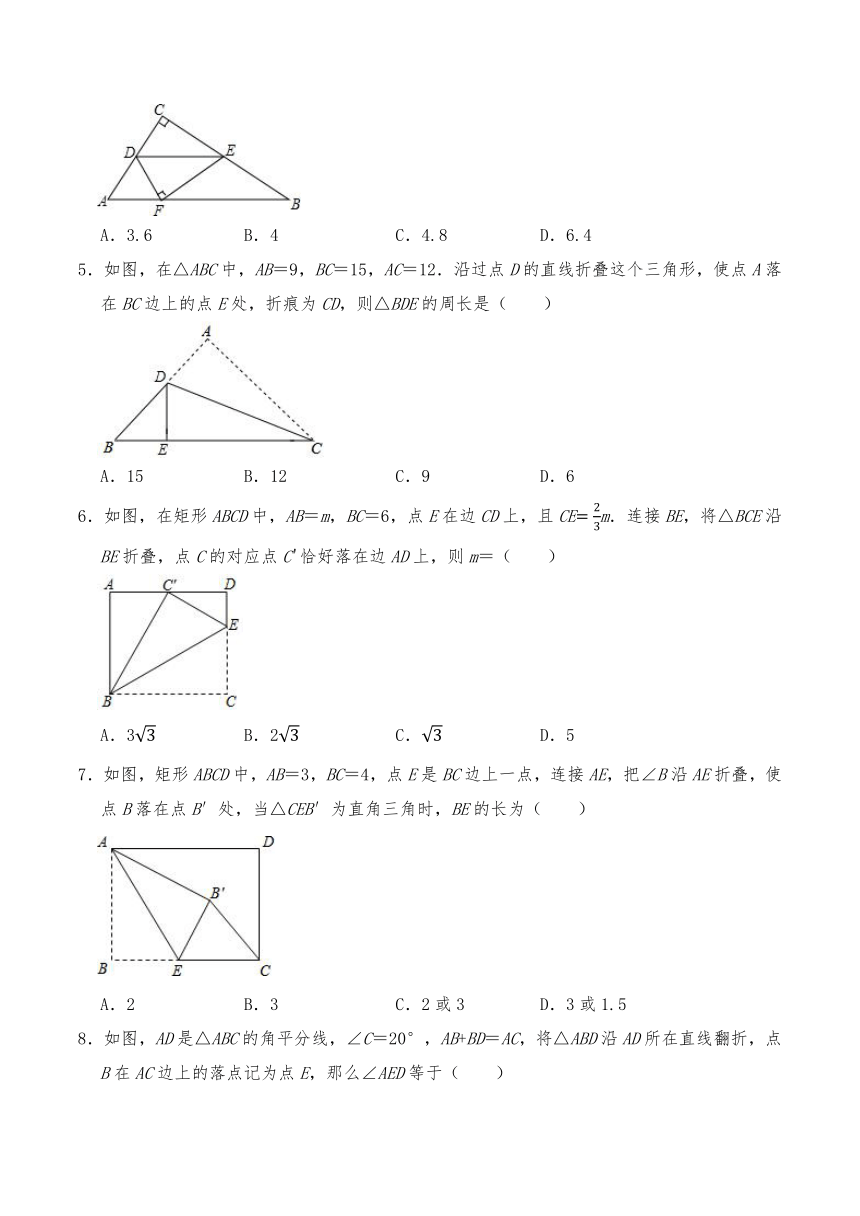
5.如图,在△ABC中,AB=9,BC=15,AC=12.沿过点D的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为CD,则△BDE的周长是( )
A.15 B.12 C.9 D.6
6.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CEm.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3 B.2 C. D.5
7.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角时,BE的长为( )
A.2 B.3 C.2或3 D.3或1.5
8.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
9.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
10.如图,矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上一动点(与A不重合),其0<AE≤2,沿BE将△ABE翻折,点A落在点P处,连接PC,有下列说法:
①△ABE和△PBE关于直线BE对称;
②线段PC的长有可能小于2;
③四边形ABPE有可能为正方形;
④当△PCD是等腰三角形时,PC=2或.
其中正确的序号是 ( )
A.①② B.①③ C.①③④ D.②③④
二、填空题
11.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为 .
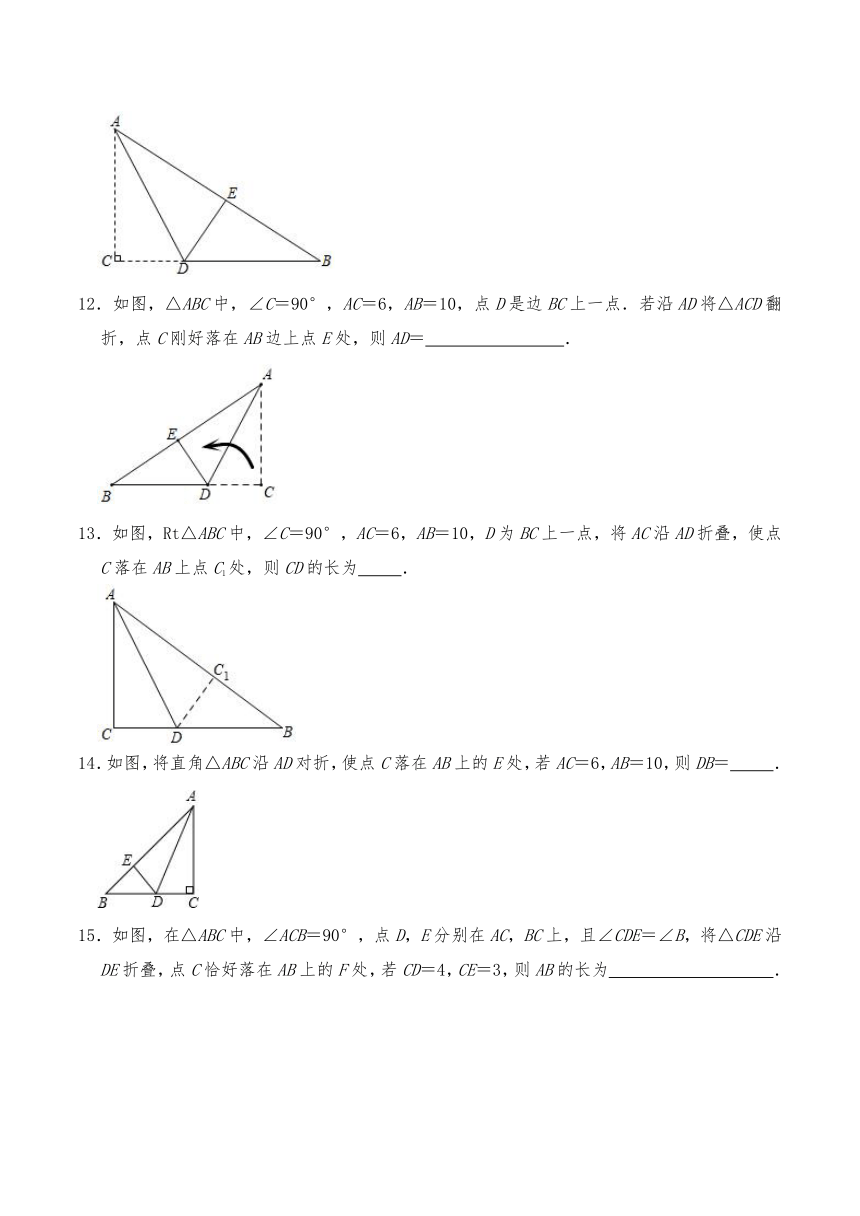
12.如图,△ABC中,∠C=90°,AC=6,AB=10,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则AD= .
13.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 .
14.如图,将直角△ABC沿AD对折,使点C落在AB上的E处,若AC=6,AB=10,则DB= .
15.如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB上的F处,若CD=4,CE=3,则AB的长为 .
16.如图,已知在△ABC中,∠C=90°,BC=2,点D是边BC的中点,∠ABC=∠CAD,将ACD沿直线AD翻折,点C落在点E处,连接BE,那么线段BE的长为 .
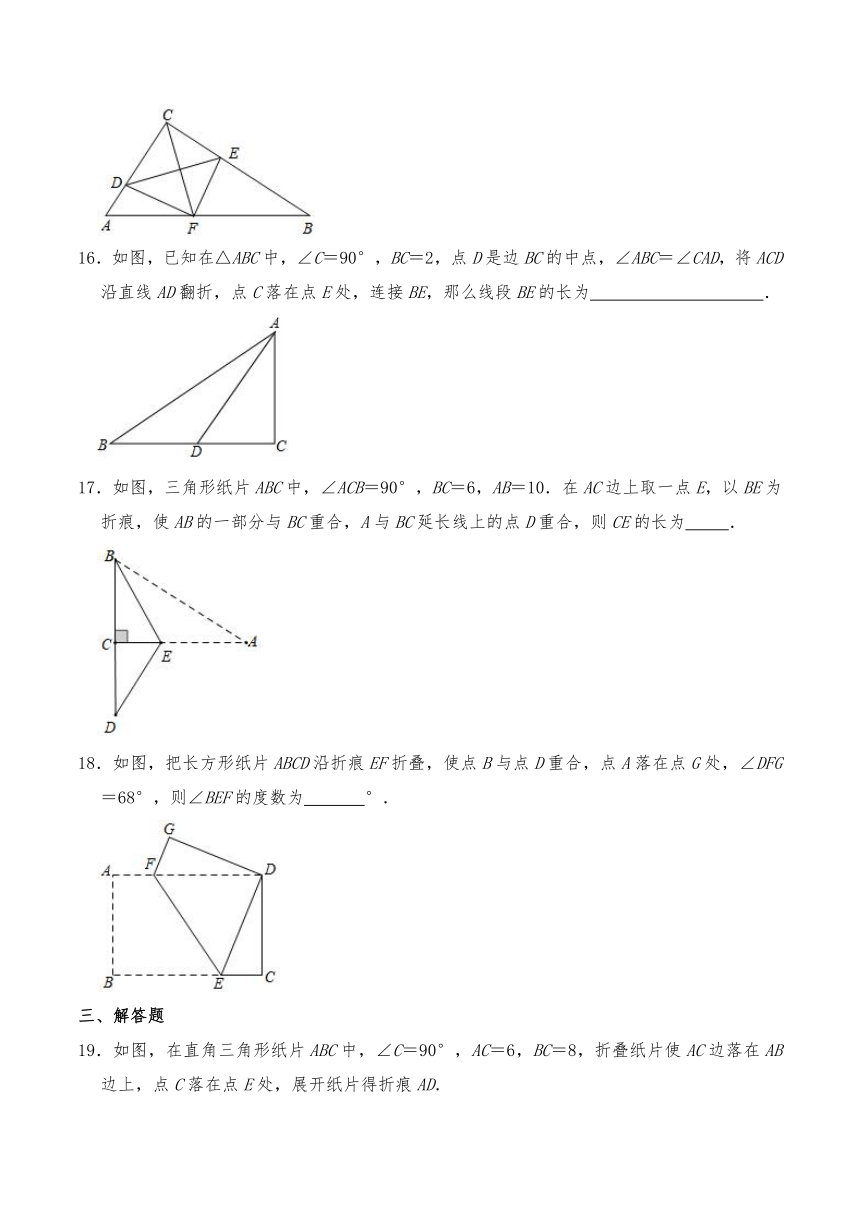
17.如图,三角形纸片ABC中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长为 .
18.如图,把长方形纸片ABCD沿折痕EF折叠,使点B与点D重合,点A落在点G处,∠DFG=68°,则∠BEF的度数为 °.
三、解答题
19.如图,在直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,折叠纸片使AC边落在AB边上,点C落在点E处,展开纸片得折痕AD.
(1)直接写出AB的长是 ;
(2)求CD的长.
20.如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
21.(1)如图1,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置(如图1),则∠EBC等于 度.
(2)如图2,有一直角三角形纸片,两直角边AC=3,BC=4,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
22.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
23.如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积;
(3)求线段AM的长度.
24.我们知道,图形的运动只改变图形的位置,不改变图形的形状、大小,运动前后的两个图形全等,翻折就是这样.如图1,将△ABC沿AD翻折,使点C落在AB边上的点C'处,则△ADC≌△ADC'.
尝试解决:
(1)如图2,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD翻折,使点C落在AB边上的点C'处,求CD的长.
(2)如图3,在长方形ABCD中,AB=8,AD=6,点P在边AD上,连接BP,将△ABP沿BP翻折,使点A落在点E处,PE、BE分别与CD交于点G、F,且DG=EG.
①求证:PE=DF;
答案
一、选择题
C.A.D.A.B.A.D.C.D.B.
二、填空题
11.12.
12.3.
13.3.
14.5.
15..
16..
17.3.
18.56.
三、解答题
19.(1)∵直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,
∴AB10,
故答案为:10;
(2)由折叠的性质可知,
AD是∠CAB的平分线,DC⊥AC,DE⊥AB,AC=AE,
∴DC=DE,
∵AC=6,AB=10,
∴AE=6,BE=4,
设CD=x,则BD=8﹣x,DE=x,
∵DE⊥BE,
∴x2+42=(8﹣x)2,
解得,x=3,
即CD的长是3.
20.(1)△ABC是直角三角形,理由如下:
在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8﹣x,
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
∴x2+16=64﹣16x+x2,
∴x=3,即CD长为3.
21.(1)依题意,得∠EDA=∠ADC=45°,即∠EDC=90°,
又∵DC=DE,AD为△ABC的中线,
∴BD=DC,即BD=DE,△BDE为等腰直角三角形,
∴∠EBC=45°;
(2)令CD=x,则DB=4﹣x,
由于是直角三角形且是折叠,所以AB=5,AE=AC=3,
DE=x,EB=2,因为∠AED=∠C=90°,
故在Rt△BDE中运用勾股定理得:
(4﹣x)2=22+x2,
16﹣8x=4,解得x,即CD.
22.(1)证明:由折叠的性质得:B'F=BF,∠B'FE=∠BFE,
在长方形纸片ABCD中,AD∥BC,
∴∠B'EF=∠BFE,
∴∠B'FE=∠B'EF,
∴B'F=B'E,
∴B'E=BF.
(2)解:a,b,c之间的关系是a2+b2=c2.理由如下:
由(1)知B'E=BF=c,
由折叠的性质得:∠A'=∠A=90°,A'E=AE=a,A'B'=AB=b.
在△A'B'E中,∵∠A'=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
23.(1)由题意设CN=x cm,则EN=(8﹣x)cm,
又∵CEDC=4cm,
∴在Rt△ECN中,EN2=EC2+CN2,即(8﹣x)2=42+x2,
解得:x=3,即CN=3cm;
(2)在Rt△DCE中,CE=4cm,CD=8cm,
由勾股定理得:DEcm,
如图,过点M作MG⊥CD于点G,则由题意可知AM=DG,MG=BC=CD.
连接DE,交MG于点I.
由折叠可知,DE⊥MN,∴∠NMG+∠MIE=90°,
∵∠DIG+∠EDC=90°,∠MIE=∠DIG(对顶角相等),
∴∠NMG=∠EDC.
在△MNG与△DEC中,
,
∴△MNG≌△DEC(ASA).
∴MN=DEcm,
∴以MN为边长的正方形的面积=(4)2=80.
(3)∵△MNG≌△DEC
∴GN=CE=4cm,
∴DG=CD﹣CN﹣GN=8﹣3﹣4=1cm.
∴AM=DG=1cm.
24.(1)∵∠C=90°,AC=6,BC=8,
∴AB10,
∵将△ABC沿AD翻折,使点C落在AB边上的点C'处,
∴△ADC≌△ADC'.
∴CD=C'D,∠AC'D=∠ACD=90°,
即∠DC'B=180°﹣∠AC'D=180°﹣90°=90°,AC=AC'=6,
∴BC'=AB﹣AC'=10﹣6=4,
∴△DC'B为直角三角形,且∠DC'B=90°,
∴C'D2+C'B2=DB2,
即CD2+42=(8﹣CD)2,
∴CD=3;
(2)①由折叠可知△PAB≌△PEB,
∴PE=PE,∠A=∠E=90°,
在△DPG和△EFG中,
,
∴△DPG≌△EFG(ASA),
∴PG=FG,
∴PG+GE=FG+GD,
即PE=DF;
②∵△PAB≌△PEB,△DPG≌△EFG,AB=8,AD=6,
∴PE=DF=PA,即CF=8﹣DF=8﹣AP,
∴EF=DP=AD﹣AP,即BF=8﹣EF=8﹣(6﹣AP)=2+AP,
∵∠C=90°,
∴BC2+CF2=BF2,
即62+(8﹣AP)2=(2+AP)2,
∴AP
一、选择题
1.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为( )
A.6 B.8 C.12 D.14
2.如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,AB=6,则△EBF周长的大小为( )
A.8 B.10 C.12 D.6
3.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A.3 B.4 C.5 D.6
4.如图,△ABC中,∠C=90°,AC=6,BC=8,D、E分别在AC、BC上且DE∥AB,将△ABC沿DE折叠,使C点落在斜边AB上的F处,则AF的长是( )
A.3.6 B.4 C.4.8 D.6.4
5.如图,在△ABC中,AB=9,BC=15,AC=12.沿过点D的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为CD,则△BDE的周长是( )
A.15 B.12 C.9 D.6
6.如图,在矩形ABCD中,AB=m,BC=6,点E在边CD上,且CEm.连接BE,将△BCE沿BE折叠,点C的对应点C'恰好落在边AD上,则m=( )
A.3 B.2 C. D.5
7.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角时,BE的长为( )
A.2 B.3 C.2或3 D.3或1.5
8.如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
A.80° B.60° C.40° D.30°
9.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
10.如图,矩形纸片ABCD,已知AB=2,BC=4,若点E是AD上一动点(与A不重合),其0<AE≤2,沿BE将△ABE翻折,点A落在点P处,连接PC,有下列说法:
①△ABE和△PBE关于直线BE对称;
②线段PC的长有可能小于2;
③四边形ABPE有可能为正方形;
④当△PCD是等腰三角形时,PC=2或.
其中正确的序号是 ( )
A.①② B.①③ C.①③④ D.②③④
二、填空题
11.如图,在△ABC中,AB=10,AC=6,BC=8,将△ABC折叠,使点C落在AB边上的点E处,AD是折痕,则△BDE的周长为 .
12.如图,△ABC中,∠C=90°,AC=6,AB=10,点D是边BC上一点.若沿AD将△ACD翻折,点C刚好落在AB边上点E处,则AD= .
13.如图,Rt△ABC中,∠C=90°,AC=6,AB=10,D为BC上一点,将AC沿AD折叠,使点C落在AB上点C1处,则CD的长为 .
14.如图,将直角△ABC沿AD对折,使点C落在AB上的E处,若AC=6,AB=10,则DB= .
15.如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB上的F处,若CD=4,CE=3,则AB的长为 .
16.如图,已知在△ABC中,∠C=90°,BC=2,点D是边BC的中点,∠ABC=∠CAD,将ACD沿直线AD翻折,点C落在点E处,连接BE,那么线段BE的长为 .
17.如图,三角形纸片ABC中,∠ACB=90°,BC=6,AB=10.在AC边上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长为 .
18.如图,把长方形纸片ABCD沿折痕EF折叠,使点B与点D重合,点A落在点G处,∠DFG=68°,则∠BEF的度数为 °.
三、解答题
19.如图,在直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,折叠纸片使AC边落在AB边上,点C落在点E处,展开纸片得折痕AD.
(1)直接写出AB的长是 ;
(2)求CD的长.
20.如图,有一个△ABC,三边长为AC=6,BC=8,AB=10,沿AD折叠,使点C落在AB边上的点E处.
(1)试判断△ABC的形状,并说明理由.
(2)求线段CD的长.
21.(1)如图1,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿AD所在直线对折,点C落在点E的位置(如图1),则∠EBC等于 度.
(2)如图2,有一直角三角形纸片,两直角边AC=3,BC=4,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
22.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处.
(1)试说明B'E=BF;
(2)设AE=a,AB=b,BF=c,试猜想a,b,c之间的关系,并说明理由.
23.如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积;
(3)求线段AM的长度.
24.我们知道,图形的运动只改变图形的位置,不改变图形的形状、大小,运动前后的两个图形全等,翻折就是这样.如图1,将△ABC沿AD翻折,使点C落在AB边上的点C'处,则△ADC≌△ADC'.
尝试解决:
(1)如图2,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿AD翻折,使点C落在AB边上的点C'处,求CD的长.
(2)如图3,在长方形ABCD中,AB=8,AD=6,点P在边AD上,连接BP,将△ABP沿BP翻折,使点A落在点E处,PE、BE分别与CD交于点G、F,且DG=EG.
①求证:PE=DF;
答案
一、选择题
C.A.D.A.B.A.D.C.D.B.
二、填空题
11.12.
12.3.
13.3.
14.5.
15..
16..
17.3.
18.56.
三、解答题
19.(1)∵直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,
∴AB10,
故答案为:10;
(2)由折叠的性质可知,
AD是∠CAB的平分线,DC⊥AC,DE⊥AB,AC=AE,
∴DC=DE,
∵AC=6,AB=10,
∴AE=6,BE=4,
设CD=x,则BD=8﹣x,DE=x,
∵DE⊥BE,
∴x2+42=(8﹣x)2,
解得,x=3,
即CD的长是3.
20.(1)△ABC是直角三角形,理由如下:
在△ABC中,∵62+82=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°;
(2)∵△ADE是△ADC沿直线AD翻折而成,
∴∠C=∠DEB=90°,CD=DE,AC=AE=6,
设CD=x,则DE=x,BD=8﹣x,
在Rt△BDE中,∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
∴x2+16=64﹣16x+x2,
∴x=3,即CD长为3.
21.(1)依题意,得∠EDA=∠ADC=45°,即∠EDC=90°,
又∵DC=DE,AD为△ABC的中线,
∴BD=DC,即BD=DE,△BDE为等腰直角三角形,
∴∠EBC=45°;
(2)令CD=x,则DB=4﹣x,
由于是直角三角形且是折叠,所以AB=5,AE=AC=3,
DE=x,EB=2,因为∠AED=∠C=90°,
故在Rt△BDE中运用勾股定理得:
(4﹣x)2=22+x2,
16﹣8x=4,解得x,即CD.
22.(1)证明:由折叠的性质得:B'F=BF,∠B'FE=∠BFE,
在长方形纸片ABCD中,AD∥BC,
∴∠B'EF=∠BFE,
∴∠B'FE=∠B'EF,
∴B'F=B'E,
∴B'E=BF.
(2)解:a,b,c之间的关系是a2+b2=c2.理由如下:
由(1)知B'E=BF=c,
由折叠的性质得:∠A'=∠A=90°,A'E=AE=a,A'B'=AB=b.
在△A'B'E中,∵∠A'=90°,
∴A'E2+A'B'2=B'E2,
∴a2+b2=c2.
23.(1)由题意设CN=x cm,则EN=(8﹣x)cm,
又∵CEDC=4cm,
∴在Rt△ECN中,EN2=EC2+CN2,即(8﹣x)2=42+x2,
解得:x=3,即CN=3cm;
(2)在Rt△DCE中,CE=4cm,CD=8cm,
由勾股定理得:DEcm,
如图,过点M作MG⊥CD于点G,则由题意可知AM=DG,MG=BC=CD.
连接DE,交MG于点I.
由折叠可知,DE⊥MN,∴∠NMG+∠MIE=90°,
∵∠DIG+∠EDC=90°,∠MIE=∠DIG(对顶角相等),
∴∠NMG=∠EDC.
在△MNG与△DEC中,
,
∴△MNG≌△DEC(ASA).
∴MN=DEcm,
∴以MN为边长的正方形的面积=(4)2=80.
(3)∵△MNG≌△DEC
∴GN=CE=4cm,
∴DG=CD﹣CN﹣GN=8﹣3﹣4=1cm.
∴AM=DG=1cm.
24.(1)∵∠C=90°,AC=6,BC=8,
∴AB10,
∵将△ABC沿AD翻折,使点C落在AB边上的点C'处,
∴△ADC≌△ADC'.
∴CD=C'D,∠AC'D=∠ACD=90°,
即∠DC'B=180°﹣∠AC'D=180°﹣90°=90°,AC=AC'=6,
∴BC'=AB﹣AC'=10﹣6=4,
∴△DC'B为直角三角形,且∠DC'B=90°,
∴C'D2+C'B2=DB2,
即CD2+42=(8﹣CD)2,
∴CD=3;
(2)①由折叠可知△PAB≌△PEB,
∴PE=PE,∠A=∠E=90°,
在△DPG和△EFG中,
,
∴△DPG≌△EFG(ASA),
∴PG=FG,
∴PG+GE=FG+GD,
即PE=DF;
②∵△PAB≌△PEB,△DPG≌△EFG,AB=8,AD=6,
∴PE=DF=PA,即CF=8﹣DF=8﹣AP,
∴EF=DP=AD﹣AP,即BF=8﹣EF=8﹣(6﹣AP)=2+AP,
∵∠C=90°,
∴BC2+CF2=BF2,
即62+(8﹣AP)2=(2+AP)2,
∴AP
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
