北师大版八年级数学上册试题 一课一练1.3勾股定理的应用-勾股定理与最短路径问题(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 一课一练1.3勾股定理的应用-勾股定理与最短路径问题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 133.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 12:49:43 | ||
图片预览



文档简介
1.3勾股定理的应用-勾股定理与最短路径问题
一、选择题
1.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁沿侧面爬行,想吃到B点的食物,需要爬行的最短路径是( )
A.9 B.13 C.14 D.25
2.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为( )
A.12cm B.14cm C.20cm D.24cm
3.如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是( )
A.5 B. C. D.4
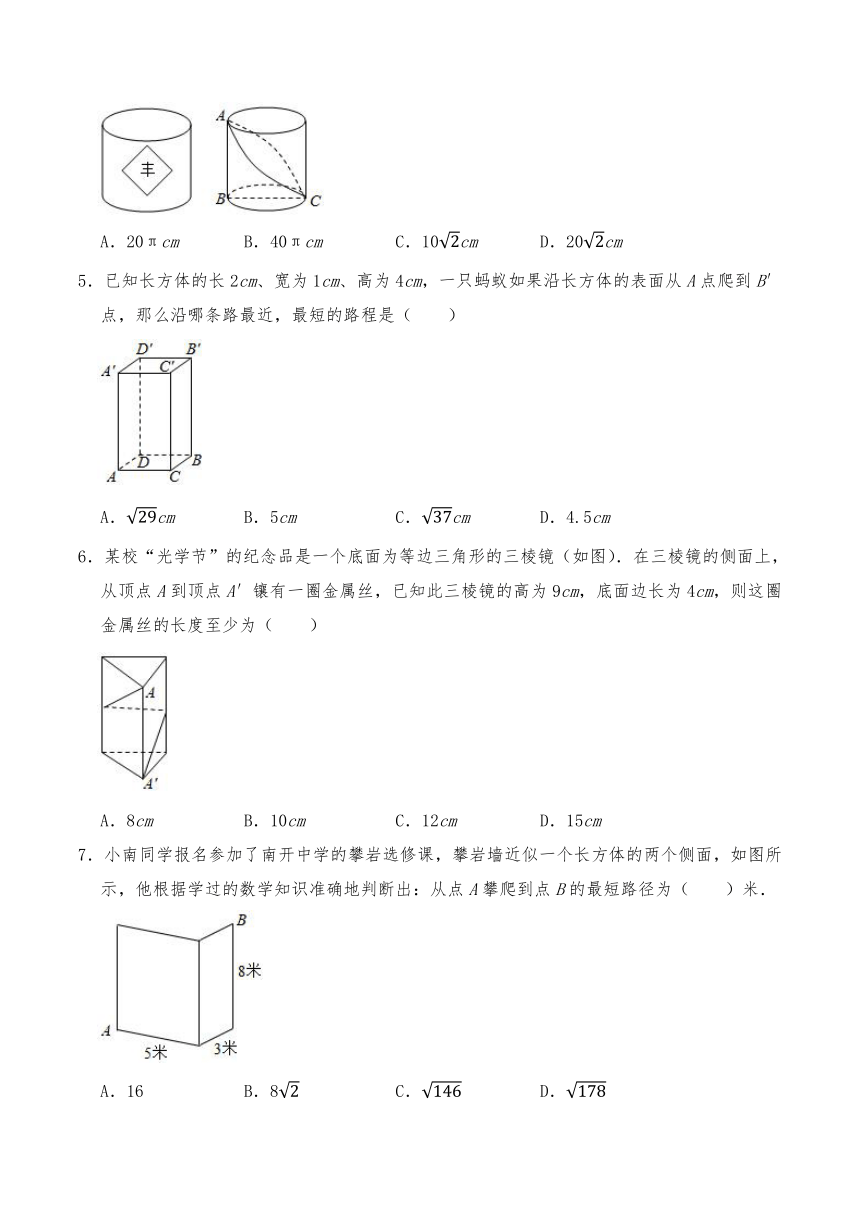
4.今年9月22日是第三个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为10cm的圆柱粮仓模型,如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.20πcm B.40πcm C.10cm D.20cm
5.已知长方体的长2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是( )
A.cm B.5cm C.cm D.4.5cm
6.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.15cm
7.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为( )米.
A.16 B.8 C. D.
8.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为( )
A. B. C.10 D.
9.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
A.10 B.50 C.120 D.130
10.如图,圆柱的高为4cm,底面半径为cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是( )cm.
A.5 B.5π C.3 D.3
二、填空题
11.如图,一个长方体盒子的长、宽、高分别为5cm、4cm、3cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.
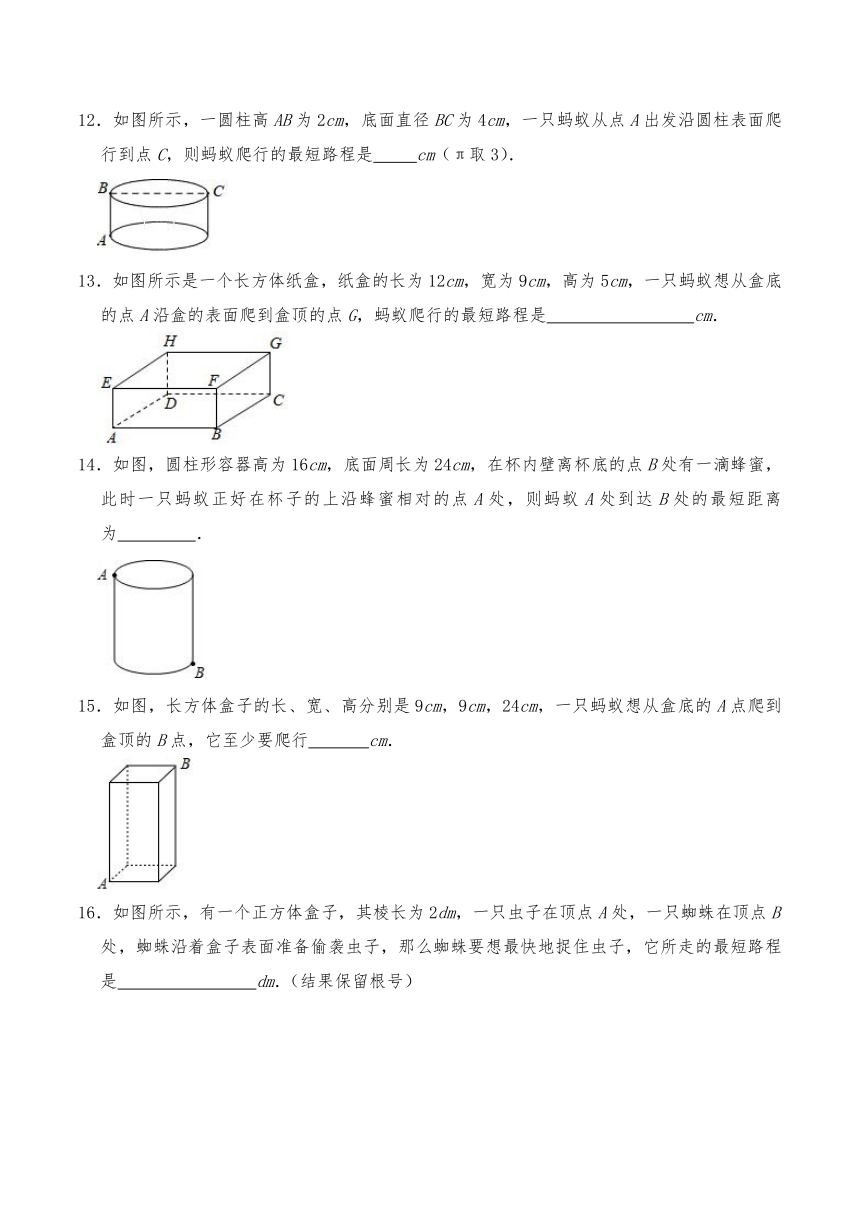
12.如图所示,一圆柱高AB为2cm,底面直径BC为4cm,一只蚂蚁从点A出发沿圆柱表面爬行到点C,则蚂蚁爬行的最短路程是 cm(π取3).
13.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.
14.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为 .
15.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.
16.如图所示,有一个正方体盒子,其棱长为2dm,一只虫子在顶点A处,一只蜘蛛在顶点B处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是 dm.(结果保留根号)
17.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24cm.则蚂蚁爬行的最短距离为 cm.
18.如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C'处,若长方体的长AB=4cm,宽BC=2cm,高BB'=1cm,则蚂蚁爬行的最短路径长是 .
三、解答题
19.如图,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
20.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?
21.如图所示,有一个圆柱,底面圆的直径AB,高BC=12cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从A点爬到P点的最短距离.
22.如图,长方体的长为20cm,宽为10cm,高为15cm,点B与点C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖.
(1)求出点A到点B的距离;
(2)求蚂蚁从点A爬到点B的最短路程是多少?
23.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为多少?
24.如图所示,一个无盖四棱柱容器,其底面是一个边长为3cm的正方形,高为20cm.现有一根彩带,从底面A点开始缠绕四棱柱,刚好缠绕4周到达B点(假设彩带完美贴合四棱柱).
(1)请问彩带的长度是多少?
(2)如图所示,一只蚂蚁在容器外A点发现容器的内部距离顶部2cm处有一滴蜂蜜,它想以最短的路程到达C处.请问蚂蚁走的最短路程是多少呢?
(注:以上两问均要画出平面展开示意图,再解答)
答案
一、选择题
B.D.A.D.B.D.B.C.B.A.
二、填空题
11..
12.6.
13.2.
14.20cm.
15.30.
16.2.
17.6.
18.5cm.
三、解答题
19.如图所示,将圆柱体侧面展开,连接AB,则AB的长即为蜘蛛爬行的最短路程.
根据题意得AC=20cm,BC=πR=5π=5×3=15cm,
在Rt△ABC中,由勾股定理得AB2=BC2+AC2=152+202=625,
所以AB=25cm,
即最短路程是25cm.
20.如图1,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴BM=18﹣6=12,BN=10+6=16,
∴MN20(cm);
如图2,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴PM=18﹣6+6=18,NP=10,
∴MN2(cm).
如图3中,
MN2(cm),
∵20<22,
∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm.
21.将圆柱体的侧面展开,如图所示:
AB底面周长π8(cm),APBC=6(cm),
所以AP10(cm),
故蚂蚁从A点爬到P点的最短距离为10cm.
22.(1)将长方体沿CF、FG、GH剪开,向右翻折,使面FCHG和面ADCH在同一个平面内,
连接AB,如图1,
由题意可得:BD=BC+CD=5+10=15cm,AD=CH=15cm,
在Rt△ABD中,根据勾股定理得:AB15cm;
将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,
连接AB,如图2,
由题意得:BH=BC+CH=5+15=20cm,AH=10cm,
在Rt△ABH中,根据勾股定理得:AB10cm,
则需要爬行的最短距离是15cm.
连接AB,如图3,
由题意可得:BB′=B′E+BE=15+10=25cm,AB′=BC=5cm,
在Rt△AB′B中,根据勾股定理得:AB5cm,
综上所述,点A到点B的距离为:15cm,10cm,5cm;
(2)由(1)知,∵点A到点B的距离为:15cm,10cm,5cm;
∴15105,
∴则需要爬行的最短距离是15cm.
23.如图:将圆柱展开,EG为上底面圆周长的一半,
作A关于E的对称点A',连接A'B交EG于F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF的长,即AF+BF=A'B=20cm,
延长BG,过A'作A'D⊥BG于D,
∵AE=A'E=DG=4cm,
∴BD=16cm,
Rt△A'DB中,由勾股定理得:A'D12(cm),
则该圆柱底面周长为24cm.
24.(1)如图,
将长方体的侧面沿AB展开,取A′B′的四等分点C、D、E,取AB的四等分点C′、D′、E′,连接B′E′,D′E,C′D,AC,
则AC+C′D+D′E+E′B′=4AC为所求的最短细线长,
∵AC2=AA′2+A′C2,AC13,
∴AC+C′D+D′E+E′B′=4AC=52,
答:彩带的长度是52cm;
(2)如图,
将四棱柱展开,找到C的对称点C′,连接AC′,则AC′即为蚂蚁走的最段路程,
在直角△AMC中,AM=6cm,MC′=20+(20﹣18)=22cm,
由勾股定理得:AC′2=AM2+MC′2=62+222=520,
则AC′=2cm,
答:蚂蚁走的最短路程是2cm.
一、选择题
1.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁沿侧面爬行,想吃到B点的食物,需要爬行的最短路径是( )
A.9 B.13 C.14 D.25
2.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为( )
A.12cm B.14cm C.20cm D.24cm
3.如图所示的圆柱体中底面圆的半径是,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是( )
A.5 B. C. D.4
4.今年9月22日是第三个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为10cm的圆柱粮仓模型,如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )
A.20πcm B.40πcm C.10cm D.20cm
5.已知长方体的长2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是( )
A.cm B.5cm C.cm D.4.5cm
6.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )
A.8cm B.10cm C.12cm D.15cm
7.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为( )米.
A.16 B.8 C. D.
8.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为( )
A. B. C.10 D.
9.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )
A.10 B.50 C.120 D.130
10.如图,圆柱的高为4cm,底面半径为cm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是( )cm.
A.5 B.5π C.3 D.3
二、填空题
11.如图,一个长方体盒子的长、宽、高分别为5cm、4cm、3cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.
12.如图所示,一圆柱高AB为2cm,底面直径BC为4cm,一只蚂蚁从点A出发沿圆柱表面爬行到点C,则蚂蚁爬行的最短路程是 cm(π取3).
13.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.
14.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为 .
15.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.
16.如图所示,有一个正方体盒子,其棱长为2dm,一只虫子在顶点A处,一只蜘蛛在顶点B处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是 dm.(结果保留根号)
17.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24cm.则蚂蚁爬行的最短距离为 cm.
18.如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C'处,若长方体的长AB=4cm,宽BC=2cm,高BB'=1cm,则蚂蚁爬行的最短路径长是 .
三、解答题
19.如图,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)
20.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?
21.如图所示,有一个圆柱,底面圆的直径AB,高BC=12cm,在BC的中点P处有一块蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从A点爬到P点的最短距离.
22.如图,长方体的长为20cm,宽为10cm,高为15cm,点B与点C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖.
(1)求出点A到点B的距离;
(2)求蚂蚁从点A爬到点B的最短路程是多少?
23.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为多少?
24.如图所示,一个无盖四棱柱容器,其底面是一个边长为3cm的正方形,高为20cm.现有一根彩带,从底面A点开始缠绕四棱柱,刚好缠绕4周到达B点(假设彩带完美贴合四棱柱).
(1)请问彩带的长度是多少?
(2)如图所示,一只蚂蚁在容器外A点发现容器的内部距离顶部2cm处有一滴蜂蜜,它想以最短的路程到达C处.请问蚂蚁走的最短路程是多少呢?
(注:以上两问均要画出平面展开示意图,再解答)
答案
一、选择题
B.D.A.D.B.D.B.C.B.A.
二、填空题
11..
12.6.
13.2.
14.20cm.
15.30.
16.2.
17.6.
18.5cm.
三、解答题
19.如图所示,将圆柱体侧面展开,连接AB,则AB的长即为蜘蛛爬行的最短路程.
根据题意得AC=20cm,BC=πR=5π=5×3=15cm,
在Rt△ABC中,由勾股定理得AB2=BC2+AC2=152+202=625,
所以AB=25cm,
即最短路程是25cm.
20.如图1,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴BM=18﹣6=12,BN=10+6=16,
∴MN20(cm);
如图2,
∵AB=18cm,BC=GF=12cm,BF=10cm,
∴PM=18﹣6+6=18,NP=10,
∴MN2(cm).
如图3中,
MN2(cm),
∵20<22,
∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm.
21.将圆柱体的侧面展开,如图所示:
AB底面周长π8(cm),APBC=6(cm),
所以AP10(cm),
故蚂蚁从A点爬到P点的最短距离为10cm.
22.(1)将长方体沿CF、FG、GH剪开,向右翻折,使面FCHG和面ADCH在同一个平面内,
连接AB,如图1,
由题意可得:BD=BC+CD=5+10=15cm,AD=CH=15cm,
在Rt△ABD中,根据勾股定理得:AB15cm;
将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,
连接AB,如图2,
由题意得:BH=BC+CH=5+15=20cm,AH=10cm,
在Rt△ABH中,根据勾股定理得:AB10cm,
则需要爬行的最短距离是15cm.
连接AB,如图3,
由题意可得:BB′=B′E+BE=15+10=25cm,AB′=BC=5cm,
在Rt△AB′B中,根据勾股定理得:AB5cm,
综上所述,点A到点B的距离为:15cm,10cm,5cm;
(2)由(1)知,∵点A到点B的距离为:15cm,10cm,5cm;
∴15105,
∴则需要爬行的最短距离是15cm.
23.如图:将圆柱展开,EG为上底面圆周长的一半,
作A关于E的对称点A',连接A'B交EG于F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF的长,即AF+BF=A'B=20cm,
延长BG,过A'作A'D⊥BG于D,
∵AE=A'E=DG=4cm,
∴BD=16cm,
Rt△A'DB中,由勾股定理得:A'D12(cm),
则该圆柱底面周长为24cm.
24.(1)如图,
将长方体的侧面沿AB展开,取A′B′的四等分点C、D、E,取AB的四等分点C′、D′、E′,连接B′E′,D′E,C′D,AC,
则AC+C′D+D′E+E′B′=4AC为所求的最短细线长,
∵AC2=AA′2+A′C2,AC13,
∴AC+C′D+D′E+E′B′=4AC=52,
答:彩带的长度是52cm;
(2)如图,
将四棱柱展开,找到C的对称点C′,连接AC′,则AC′即为蚂蚁走的最段路程,
在直角△AMC中,AM=6cm,MC′=20+(20﹣18)=22cm,
由勾股定理得:AC′2=AM2+MC′2=62+222=520,
则AC′=2cm,
答:蚂蚁走的最短路程是2cm.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
