勾股定理(二)[上学期]
文档属性
| 名称 | 勾股定理(二)[上学期] | 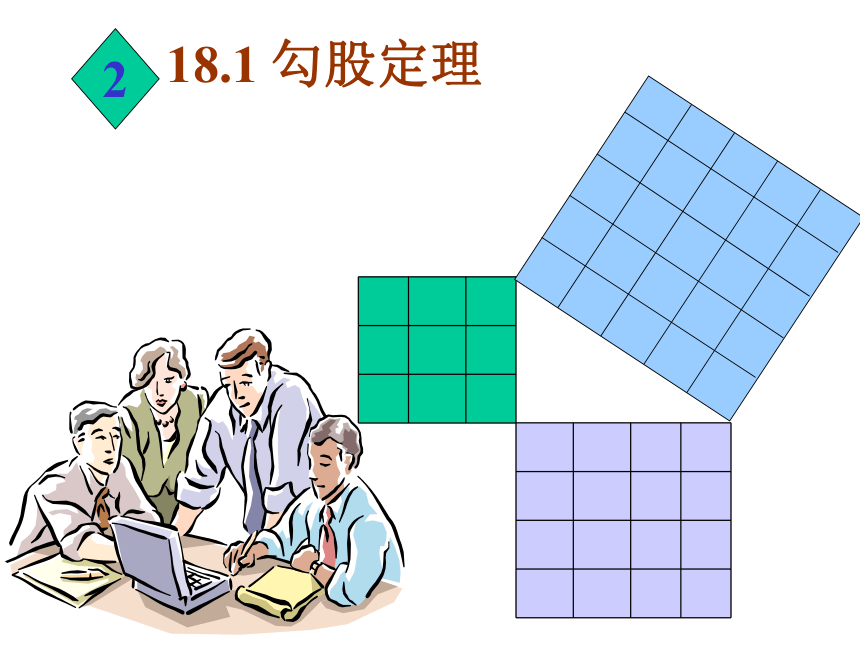 | |
| 格式 | rar | ||
| 文件大小 | 469.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-16 18:15:00 | ||
图片预览

文档简介
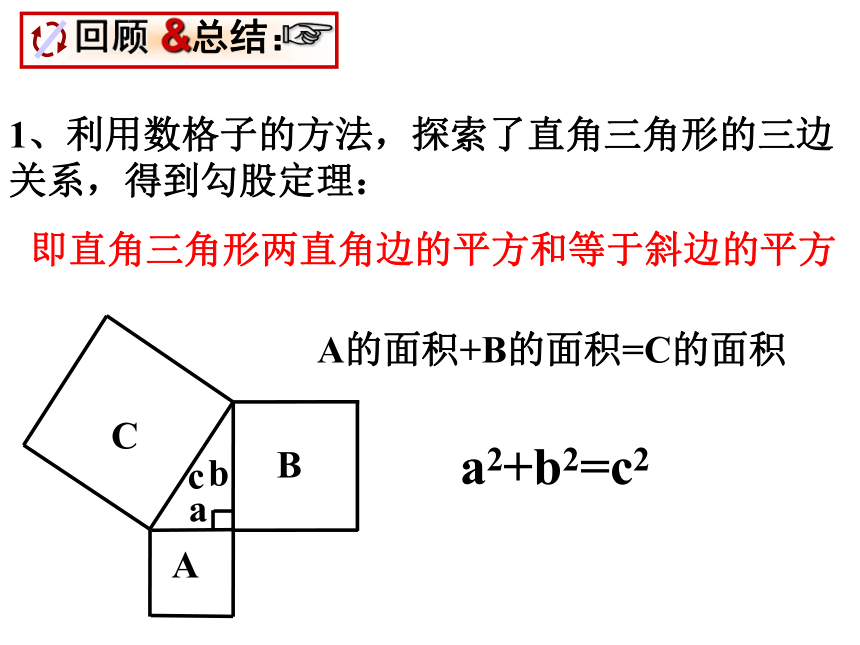
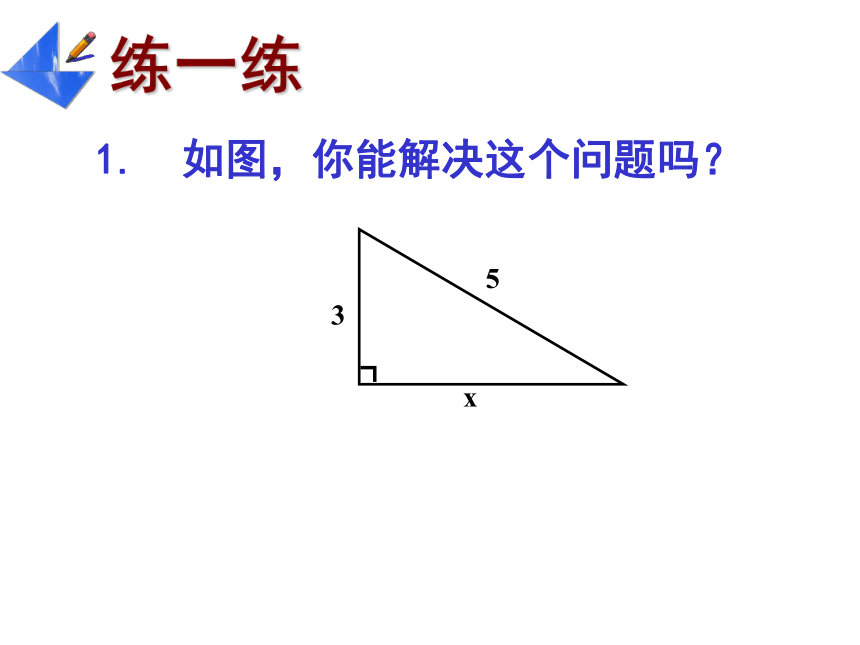
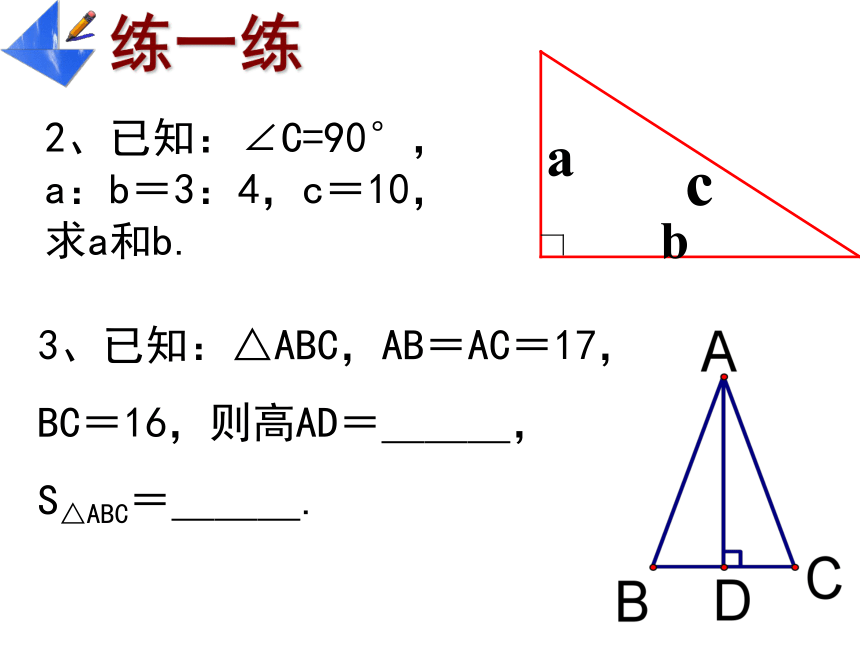
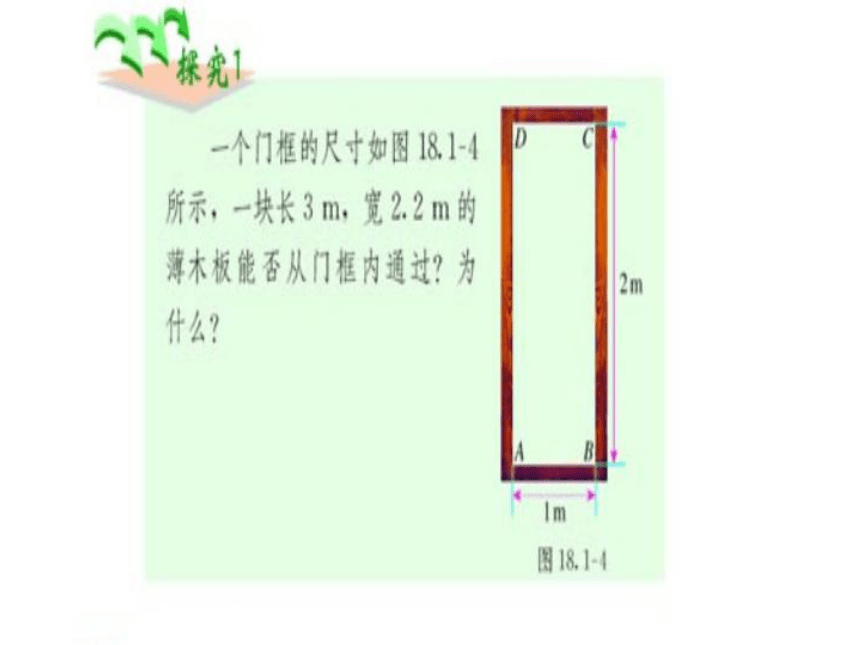
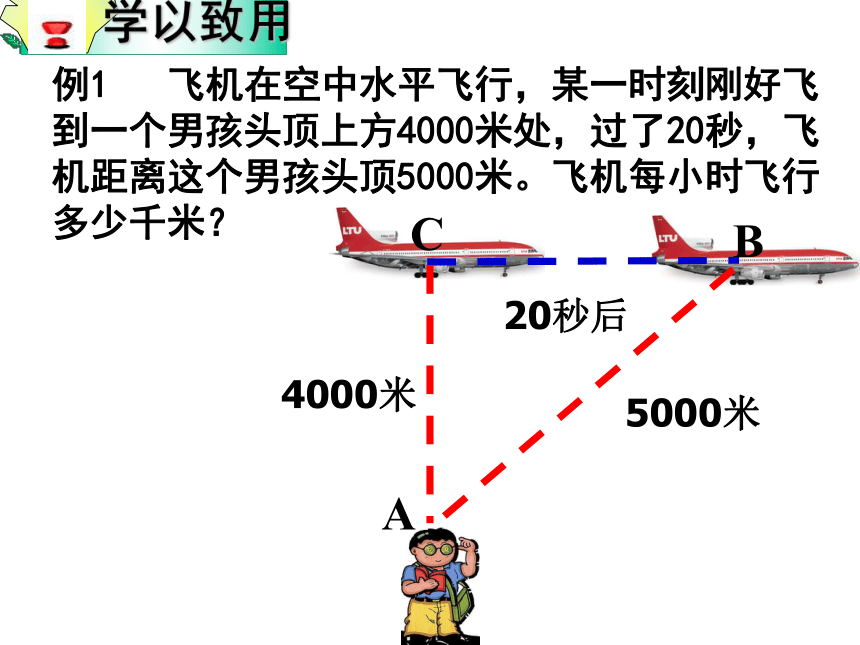
课件15张PPT。18.1 勾股定理21、利用数格子的方法,探索了直角三角形的三边关系,得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2 1. 如图,你能解决这个问题吗?2、已知:∠C=90°,a:b=3:4,c=10,求a和b.3、已知:△ABC,AB=AC=17,
BC=16,则高AD=___,
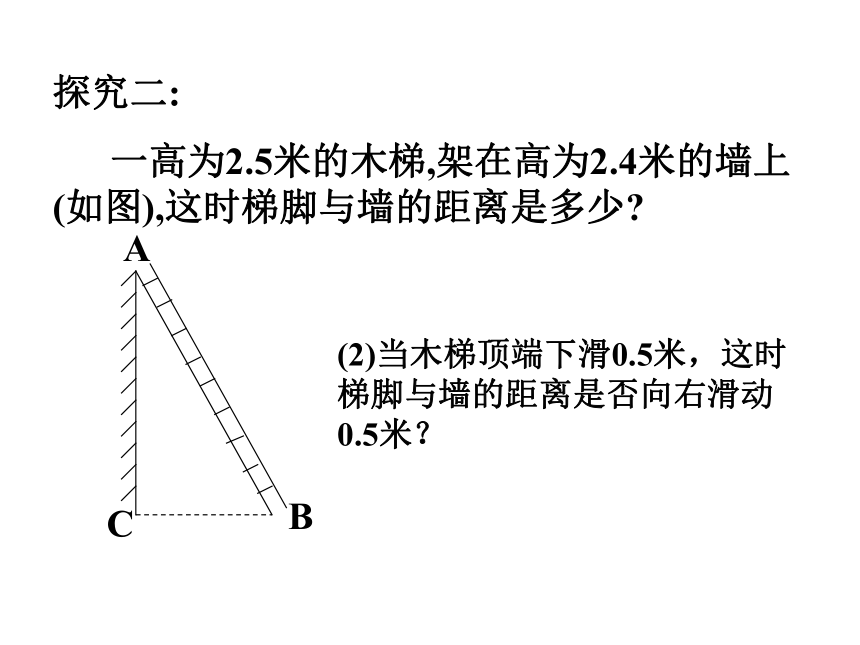
S△ABC=___.例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每小时飞行多少千米?A4000米5000米20秒后BC探究二:
一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? (2)当木梯顶端下滑0.5米,这时梯脚与墙的距离是否向右滑动0.5米?1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CD例1: 已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=81、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和练习1.在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;3.如图,在△ABC中,∠C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?(3)若c=25,b=15,则 a = ;202.等边三角形边长为10,求它的高及面积。ba试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABCDA4、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE
BC=16,则高AD=___,
S△ABC=___.例1 飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每小时飞行多少千米?A4000米5000米20秒后BC探究二:
一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? (2)当木梯顶端下滑0.5米,这时梯脚与墙的距离是否向右滑动0.5米?1、放学以后,小红和小颖从学校分手,分别沿着东方向和南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米,那么斜边上的高是 ( )
A、6厘米 B、 8厘米
C、 80/13厘米; D、 60/13厘米; CD例1: 已知等边三角形ABC的边长6cm, (1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°∴BD= AD=4在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=81、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形E的边长为7cm,求正方形A,B,C,D的面积的和练习1.在△ABC中,∠C=90°.(1)若a=6,c=10,则b= ;(2)若a=12,b=9,则c = ;3.如图,在△ABC中,∠C=90°,CD为斜边AB上的高,你可以得出哪些与边有关的结论?(3)若c=25,b=15,则 a = ;202.等边三角形边长为10,求它的高及面积。ba试一试: 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?DABCDA4、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE
