勾股定理应用1[下学期]
文档属性
| 名称 | 勾股定理应用1[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 104.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-20 00:00:00 | ||
图片预览


文档简介
课件10张PPT。勾股定理的应用学习目标:
1.运用勾股定理进行简单的计算
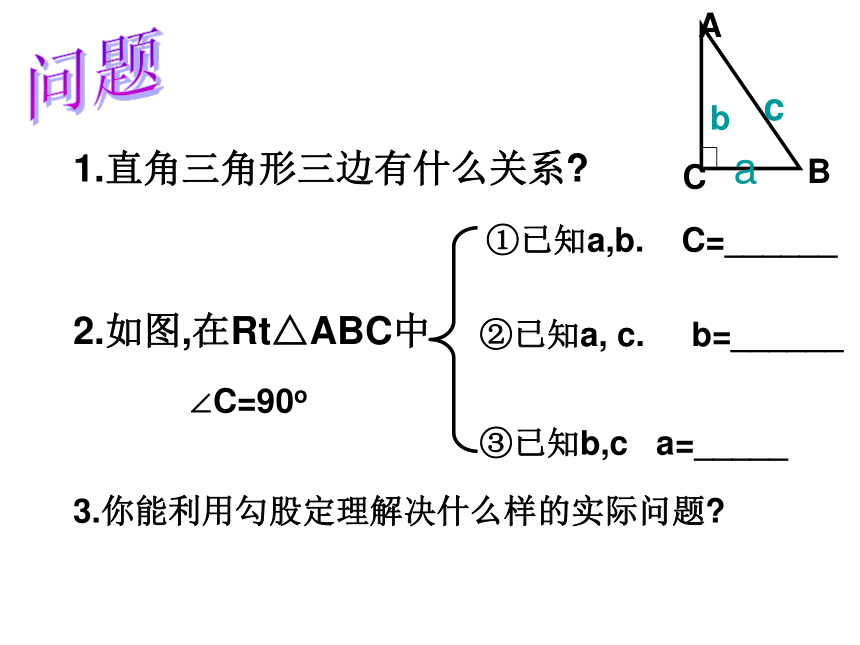
2.运用勾股定理解释生活中的实际问题.学习指导:请同学们看课本74—75页探究1、探究2.五分钟后检查提问.问题1.直角三角形三边有什么关系?
2.如图,在Rt△ABC中
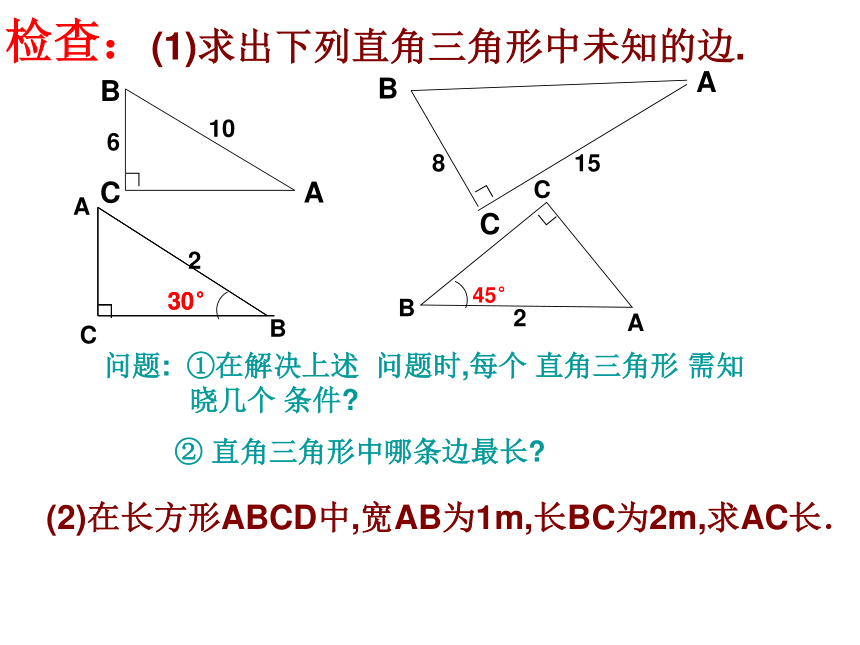
∠C=90o①已知a,b. C=______②已知a, c. b=______③已知b,c a=_____3.你能利用勾股定理解决什么样的实际问题?(1)求出下列直角三角形中未知的边.问题: ①在解决上述 问题时,每个 直角三角形 需知 晓几个 条件?
② 直角三角形中哪条边最长?
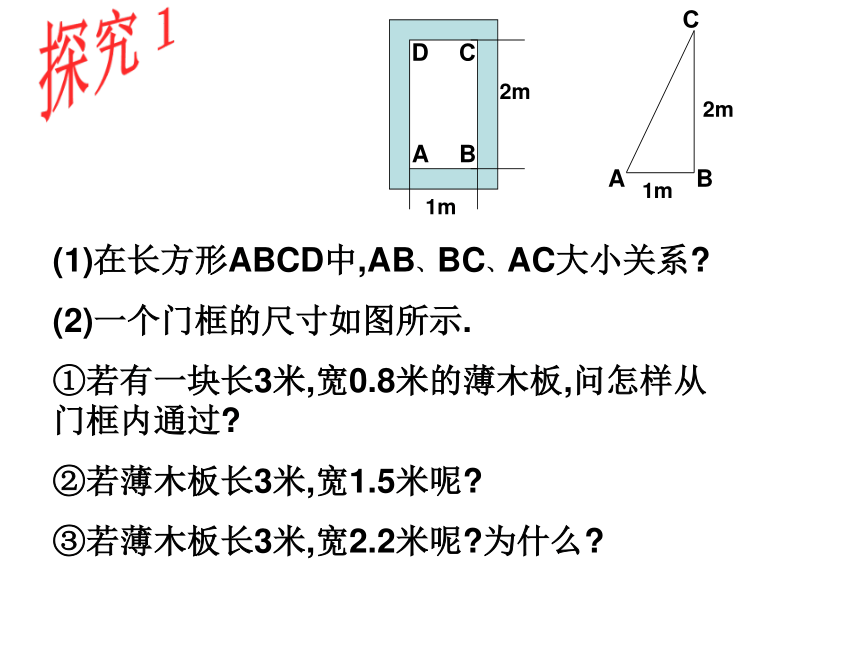
检查:(2)在长方形ABCD中,宽AB为1m,长BC为2m,求AC长. (1)在长方形ABCD中,AB、BC、AC大小关系?
(2)一个门框的尺寸如图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框内通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?探究1探究2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙下滑0.5m至c,请同学们
猜一猜,那么梯子底端B也外移0.5m吗?
算一算,底端滑动的距离近似值(保留两位小数)在Rt△AOB中oB2=______________oB=______________在Rt△COD中OD2=______________OD=________________BD=_______________梯子的顶端沿墙下滑,梯子底端外移__解AB2-AO2≈1.658mCD2-CO2≈2.236mOD-OB≈0.58m0.58m同学们,想一想,这节课你有什么收获?思考:如图:正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?
1.运用勾股定理进行简单的计算
2.运用勾股定理解释生活中的实际问题.学习指导:请同学们看课本74—75页探究1、探究2.五分钟后检查提问.问题1.直角三角形三边有什么关系?
2.如图,在Rt△ABC中
∠C=90o①已知a,b. C=______②已知a, c. b=______③已知b,c a=_____3.你能利用勾股定理解决什么样的实际问题?(1)求出下列直角三角形中未知的边.问题: ①在解决上述 问题时,每个 直角三角形 需知 晓几个 条件?
② 直角三角形中哪条边最长?
检查:(2)在长方形ABCD中,宽AB为1m,长BC为2m,求AC长. (1)在长方形ABCD中,AB、BC、AC大小关系?
(2)一个门框的尺寸如图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框内通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?探究1探究2如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙下滑0.5m至c,请同学们
猜一猜,那么梯子底端B也外移0.5m吗?
算一算,底端滑动的距离近似值(保留两位小数)在Rt△AOB中oB2=______________oB=______________在Rt△COD中OD2=______________OD=________________BD=_______________梯子的顶端沿墙下滑,梯子底端外移__解AB2-AO2≈1.658mCD2-CO2≈2.236mOD-OB≈0.58m0.58m同学们,想一想,这节课你有什么收获?思考:如图:正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?
