16.1.1二次根式的概念 课件
图片预览







文档简介
(共25张PPT)
人教版初中数学八年级下册
16.1.1二次根式的概念及定义
1.复习导入
2.新知授受
3.理解巩固
4.课堂小结
5.课后作业
教学目标
重点难点
1.知识与技能目标:掌握二次根式的定义及概念
2.过程与方法目标:掌握算术平方根与二次根式的联系
3.情感态度和价值观:树立正确的数学分析过程,提高自己的数感及符号意识
重点:从算术平方根的角度理解二次根式的概念,能够判断一个式子是否为二次根式
难点:通过二次根式的双重非负性求未知数的取值范围
复习导入
1.平方根的概念是什么?
性质
正数有两个平方根,互为相反数;
0的平方根是0;
负数没有平方根。
2.算术平方根的概念是什么?
性质
正数只有一个算术平方根,
0的算术平方根是0;
负数没有平方根。
问题引入
1.如图这张海报带给我们激情和对生活的憧憬。假设这张正方形海报的面积为5,那么它的边长是_________,面积为S的正方形边长是_________。
问题引入
思考:a可不可以等于-2?
问题引入
思考:能量E可以是负值?
人在平坦的地面上跑步,所累积的能量E与人自身的质量m和速度v的关系式为: ,如果用含m和E的式子表示v,则v=_________。
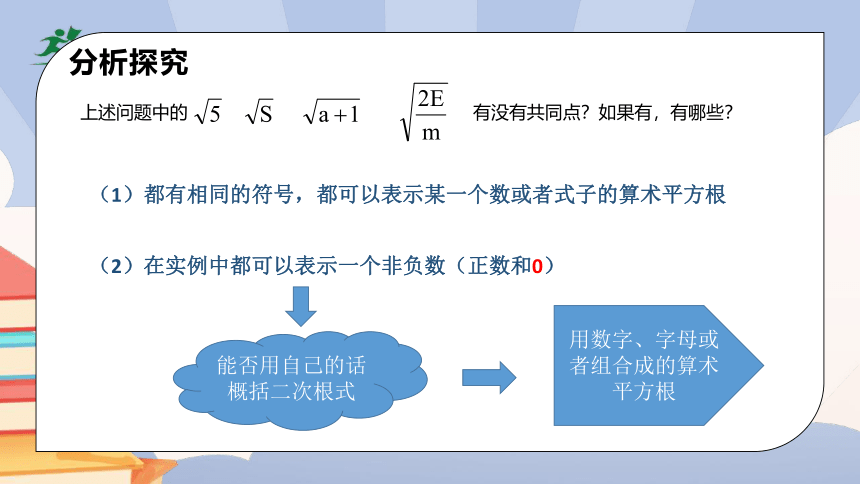
上述问题中的 有没有共同点?如果有,有哪些?
分析探究
(1)都有相同的符号,都可以表示某一个数或者式子的算术平方根
(2)在实例中都可以表示一个非负数(正数和0)
能否用自己的话概括二次根式
用数字、字母或者组合成的算术平方根
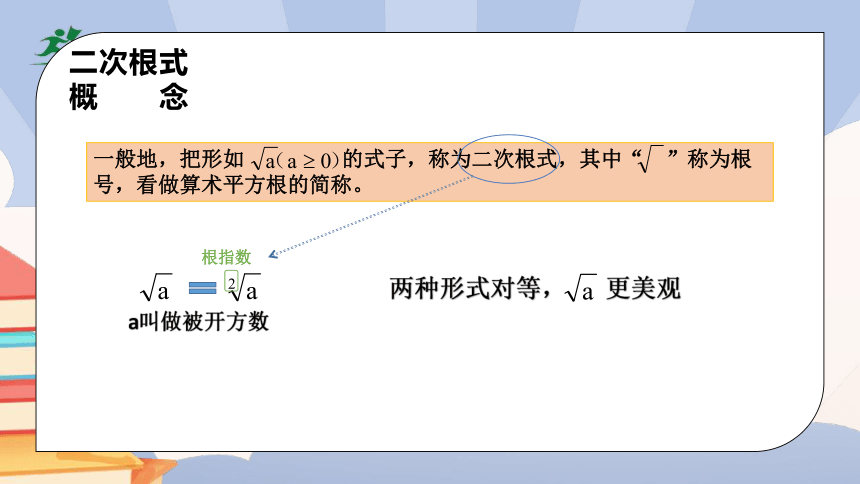
二次根式概念
一般地,把形如 的式子,称为二次根式,其中“ ”称为根号,看做算术平方根的简称。
根指数
深化概念
一般地,把形如 的式子,称为二次根式,其中“ ”称为根号,看做算术平方根的简称。
a不仅仅可以是一个数字,也可以是一个字母或者数字与字母的积与商
探究分析
是二次根式吗
答:这表示了两项之和,不满足二次根式定义
判断下面的式子哪些属于二次根式?
例题练习1
(3)
(2)
(1)
(4)
(5)
(6)
(8)
(7)
×
×
×
×
√
√
√
√
1.根指数要为2
判断二次根式的几个要素
2.被开方数整体要≥0
①多个字母型
②负数平方型
③非负平方型(无论n取什么值,被开方数整体都≥0)
例题探究1
解题分析:把x+2看成整体的被开方数,满足二次根式定义即可
解:要使式子在实数范围有意义,
必须 x+2≥0,
∴ x≥-2。
双重非负性
二次根式双重非负性
思维提升
当x 是怎样的实数时, 在实数范围内有意义?
解题分析:此时应分布满足二次根式有意义的成立条件,最终取共同的范围
解:要让式子 在实数范围有意义,
则x≥0,且x-2≥0,且分母 ≥0
所以x>2
课堂练习1
解:(1)由a+1≥0,得 a≥-1;
(2)由1-2a>0,得 a< ;
(3)由 ≥0,得 a为任何实数.
a 取何值时,下列根式有意义?
课堂练习2
若式子 有意义,则x的取值范围是( )
A、x≤2
B、x≥1
C、1≤x≤2
D、x≥2
解:要使式子在实数范围有意义,
必须 2-x≥0,x-1≥0同时成立
∴ 1≤x≤2
C
总结归纳
二次根式中求未知数的取值范围:
1.整体的被开方数≥0
2.在分母位置有关的式子都要≠0
最后利用不等式组求不等式的解集不要漏掉答案和范围
例题-非负数之和题型
解题分析:看起来式子复杂,但实际上是两个非负数之和,和为0,则每一个式子都要为0
非负数之和变式
解题分析:题目变成含x与y的关系式子,但实际上仍满足非负数之和的原理
二元一次方程组消元
巩固提升
解析:A项不管a取值多少,被开方数总大于零,D正好相反
B项被开方数小于0,C组不确定,∴正确答案为A
A
解:要使式子在实数范围有意义,
必须 x+3≥0,x-2≠0同时成立
∴ x≥-3且x≠2
解析:由题意,根据二次根式成立条件,
∴2x-5≥0,2x-5≤0
∴2x-5=0,即x=2.5∴y=0-3=-3,2xy=-15
-15
课堂小结
1.二次根式的定义及概念
一般地,我们把形如 (a≥0)的式子叫做二次
根式,“ ”称为二次根号.
2.二次根式的双重非负性
二次根式双重非负性
判断未知数的取值范围
3.二次根式的拓展应用
判断是否具备二次根式的条件
非负数的应用:先确定未知数范围,再求值
课程结束
人教版初中数学八年级下册
16.1.1二次根式的概念及定义
1.复习导入
2.新知授受
3.理解巩固
4.课堂小结
5.课后作业
教学目标
重点难点
1.知识与技能目标:掌握二次根式的定义及概念
2.过程与方法目标:掌握算术平方根与二次根式的联系
3.情感态度和价值观:树立正确的数学分析过程,提高自己的数感及符号意识
重点:从算术平方根的角度理解二次根式的概念,能够判断一个式子是否为二次根式
难点:通过二次根式的双重非负性求未知数的取值范围
复习导入
1.平方根的概念是什么?
性质
正数有两个平方根,互为相反数;
0的平方根是0;
负数没有平方根。
2.算术平方根的概念是什么?
性质
正数只有一个算术平方根,
0的算术平方根是0;
负数没有平方根。
问题引入
1.如图这张海报带给我们激情和对生活的憧憬。假设这张正方形海报的面积为5,那么它的边长是_________,面积为S的正方形边长是_________。
问题引入
思考:a可不可以等于-2?
问题引入
思考:能量E可以是负值?
人在平坦的地面上跑步,所累积的能量E与人自身的质量m和速度v的关系式为: ,如果用含m和E的式子表示v,则v=_________。
上述问题中的 有没有共同点?如果有,有哪些?
分析探究
(1)都有相同的符号,都可以表示某一个数或者式子的算术平方根
(2)在实例中都可以表示一个非负数(正数和0)
能否用自己的话概括二次根式
用数字、字母或者组合成的算术平方根
二次根式概念
一般地,把形如 的式子,称为二次根式,其中“ ”称为根号,看做算术平方根的简称。
根指数
深化概念
一般地,把形如 的式子,称为二次根式,其中“ ”称为根号,看做算术平方根的简称。
a不仅仅可以是一个数字,也可以是一个字母或者数字与字母的积与商
探究分析
是二次根式吗
答:这表示了两项之和,不满足二次根式定义
判断下面的式子哪些属于二次根式?
例题练习1
(3)
(2)
(1)
(4)
(5)
(6)
(8)
(7)
×
×
×
×
√
√
√
√
1.根指数要为2
判断二次根式的几个要素
2.被开方数整体要≥0
①多个字母型
②负数平方型
③非负平方型(无论n取什么值,被开方数整体都≥0)
例题探究1
解题分析:把x+2看成整体的被开方数,满足二次根式定义即可
解:要使式子在实数范围有意义,
必须 x+2≥0,
∴ x≥-2。
双重非负性
二次根式双重非负性
思维提升
当x 是怎样的实数时, 在实数范围内有意义?
解题分析:此时应分布满足二次根式有意义的成立条件,最终取共同的范围
解:要让式子 在实数范围有意义,
则x≥0,且x-2≥0,且分母 ≥0
所以x>2
课堂练习1
解:(1)由a+1≥0,得 a≥-1;
(2)由1-2a>0,得 a< ;
(3)由 ≥0,得 a为任何实数.
a 取何值时,下列根式有意义?
课堂练习2
若式子 有意义,则x的取值范围是( )
A、x≤2
B、x≥1
C、1≤x≤2
D、x≥2
解:要使式子在实数范围有意义,
必须 2-x≥0,x-1≥0同时成立
∴ 1≤x≤2
C
总结归纳
二次根式中求未知数的取值范围:
1.整体的被开方数≥0
2.在分母位置有关的式子都要≠0
最后利用不等式组求不等式的解集不要漏掉答案和范围
例题-非负数之和题型
解题分析:看起来式子复杂,但实际上是两个非负数之和,和为0,则每一个式子都要为0
非负数之和变式
解题分析:题目变成含x与y的关系式子,但实际上仍满足非负数之和的原理
二元一次方程组消元
巩固提升
解析:A项不管a取值多少,被开方数总大于零,D正好相反
B项被开方数小于0,C组不确定,∴正确答案为A
A
解:要使式子在实数范围有意义,
必须 x+3≥0,x-2≠0同时成立
∴ x≥-3且x≠2
解析:由题意,根据二次根式成立条件,
∴2x-5≥0,2x-5≤0
∴2x-5=0,即x=2.5∴y=0-3=-3,2xy=-15
-15
课堂小结
1.二次根式的定义及概念
一般地,我们把形如 (a≥0)的式子叫做二次
根式,“ ”称为二次根号.
2.二次根式的双重非负性
二次根式双重非负性
判断未知数的取值范围
3.二次根式的拓展应用
判断是否具备二次根式的条件
非负数的应用:先确定未知数范围,再求值
课程结束
