人教版六年级数学下册5 数学广角——鸽巢问题 课件(共21张PPT)
文档属性
| 名称 | 人教版六年级数学下册5 数学广角——鸽巢问题 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 13:27:10 | ||
图片预览







文档简介
(共21张PPT)
5 数学广角——鸽巢问题
学习目标
1.经历操作、观察、比较、说理等教 学活动,初步了解“鸽巢原理”。
2.会运用“鸽巢原理”解决一些简单的实际问题。
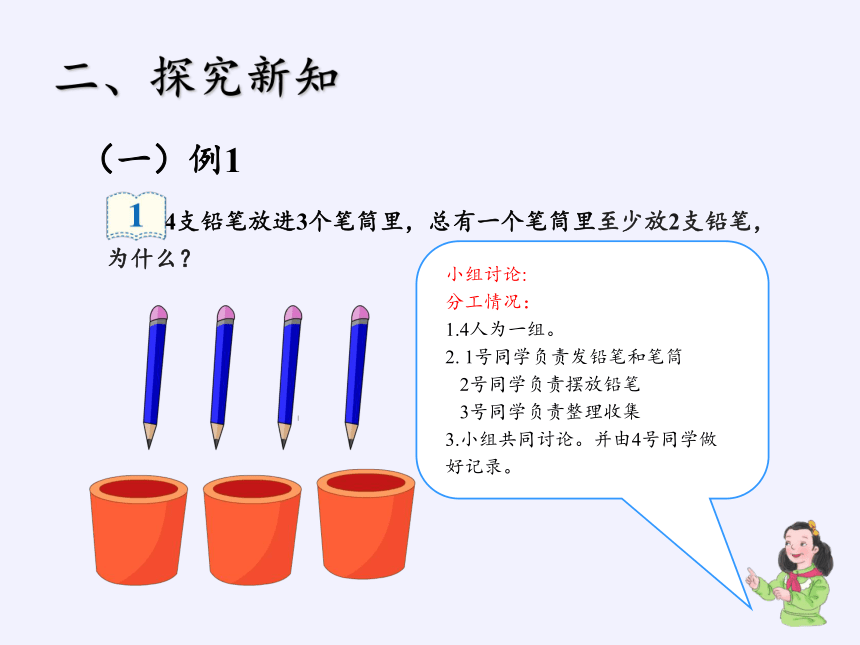
把4支铅笔放进3个笔筒里,总有一个笔筒里至少放2支铅笔,为什么?
二、探究新知
(一)例1
小组讨论:
分工情况:
1.4人为一组。
2. 1号同学负责发铅笔和笔筒
2号同学负责摆放铅笔
3号同学负责整理收集
3.小组共同讨论。并由4号同学做好记录。
把5支铅笔放进4个笔筒中呢?
......
请你想一想
只要铅笔数量是笔筒数量的1倍多(没有两倍),总有一个笔筒里至少放进2支铅笔。
?
七只鸽子飞回五个鸽舍,至少有两只鸽子飞回同一个鸽舍里,为什么?
随堂练习
二、探究新知
如果有8本书会怎么样呢?
10本呢?
7÷3=2……1
8÷3=2……2
10÷3=3……1
(二)例2
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
3. 5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1……1
1+1=2
三、知识应用
(一)做一做
想一想,商1和余数1各表示什么?
随意找13位老师,他们中至少有2个人的属相相同。为什么?
13÷12=1……1
1+1=2
三、知识应用
(二)解决问题
为什么要用1+1呢?
现在最流行用星座来测性格,用星座来测运势,你信吗?
为什么?
我们要相信科学
用科学的眼光去看待问题
用科学的方式去分析问题
用科学的方法去解决问题
你知道吗?
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄利克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄利克雷原理”。
抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进了2只鸽子,所以也称为“鸽巢原理”。
请你想一想
?
通过学习你有什么收获
四、布置作业
作业:第71页练习十三,第2题、第3题。
左右一个人成功的,不是能力,而是选择。
结束语
谢 谢
5 数学广角——鸽巢问题
学习目标
1.经历操作、观察、比较、说理等教 学活动,初步了解“鸽巢原理”。
2.会运用“鸽巢原理”解决一些简单的实际问题。
把4支铅笔放进3个笔筒里,总有一个笔筒里至少放2支铅笔,为什么?
二、探究新知
(一)例1
小组讨论:
分工情况:
1.4人为一组。
2. 1号同学负责发铅笔和笔筒
2号同学负责摆放铅笔
3号同学负责整理收集
3.小组共同讨论。并由4号同学做好记录。
把5支铅笔放进4个笔筒中呢?
......
请你想一想
只要铅笔数量是笔筒数量的1倍多(没有两倍),总有一个笔筒里至少放进2支铅笔。
?
七只鸽子飞回五个鸽舍,至少有两只鸽子飞回同一个鸽舍里,为什么?
随堂练习
二、探究新知
如果有8本书会怎么样呢?
10本呢?
7÷3=2……1
8÷3=2……2
10÷3=3……1
(二)例2
7本书放进3个抽屉,有一个抽屉至少放3本书。8本书……
你是这样想的吗?你有什么发现?
3. 5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
5÷4=1……1
1+1=2
三、知识应用
(一)做一做
想一想,商1和余数1各表示什么?
随意找13位老师,他们中至少有2个人的属相相同。为什么?
13÷12=1……1
1+1=2
三、知识应用
(二)解决问题
为什么要用1+1呢?
现在最流行用星座来测性格,用星座来测运势,你信吗?
为什么?
我们要相信科学
用科学的眼光去看待问题
用科学的方式去分析问题
用科学的方法去解决问题
你知道吗?
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄利克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄利克雷原理”。
抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进了2只鸽子,所以也称为“鸽巢原理”。
请你想一想
?
通过学习你有什么收获
四、布置作业
作业:第71页练习十三,第2题、第3题。
左右一个人成功的,不是能力,而是选择。
结束语
谢 谢
