六年级数学下册课件-6.2.1 图形的认识与测量-人教版(共14张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.2.1 图形的认识与测量-人教版(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 394.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 13:36:12 | ||
图片预览



文档简介
(共14张PPT)
图形的认识与测量
—平面图形复面图形
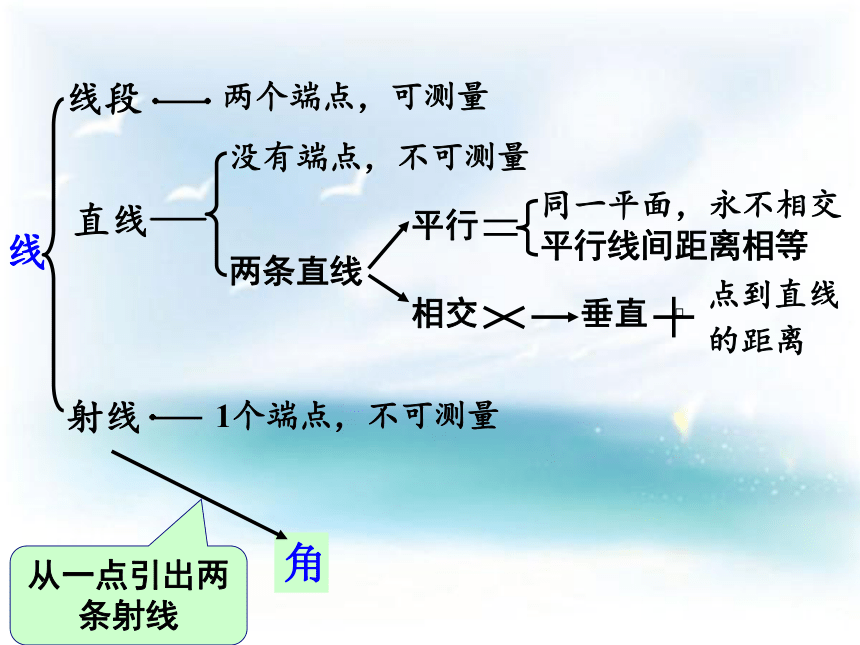
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
线
线段
直线
射线
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面,永不相交
平行线间距离相等
垂直
点到直线
的距离
角
从一点引出两条射线
1个端点,不可测量
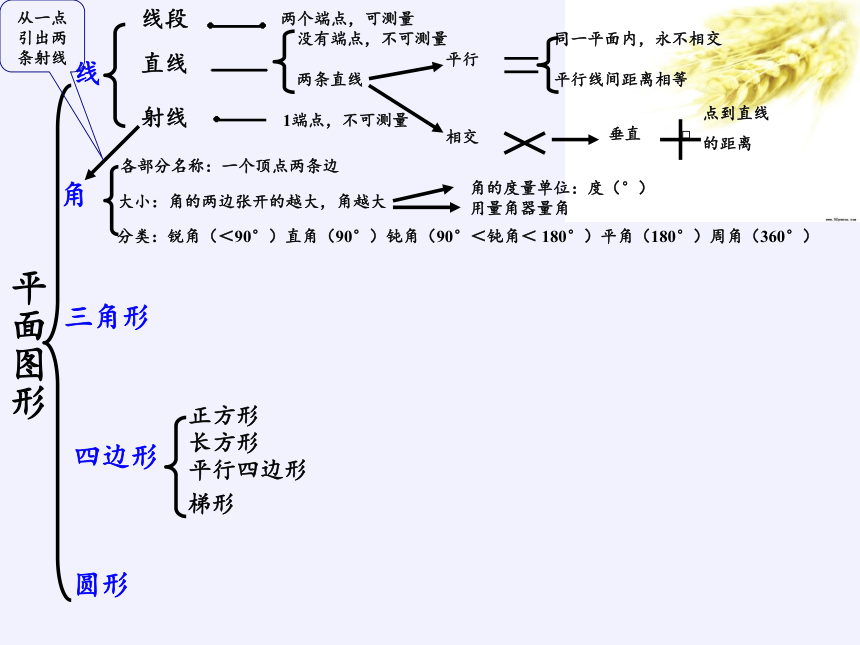
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
从一点引出两条射线
1端点,不可测量
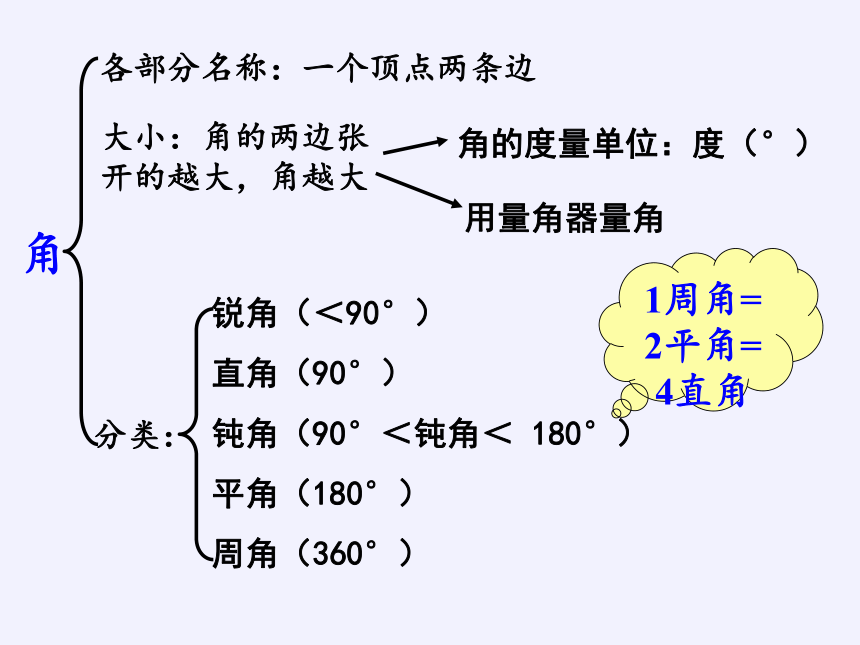
角
各部分名称:一个顶点两条边
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
分类:
锐角(<90°)
直角(90°)
钝角(90°<钝角< 180°)
平角(180°)
周角(360°)
1周角=
2平角=
4直角
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
从一点引出两条射线
1端点,不可测量
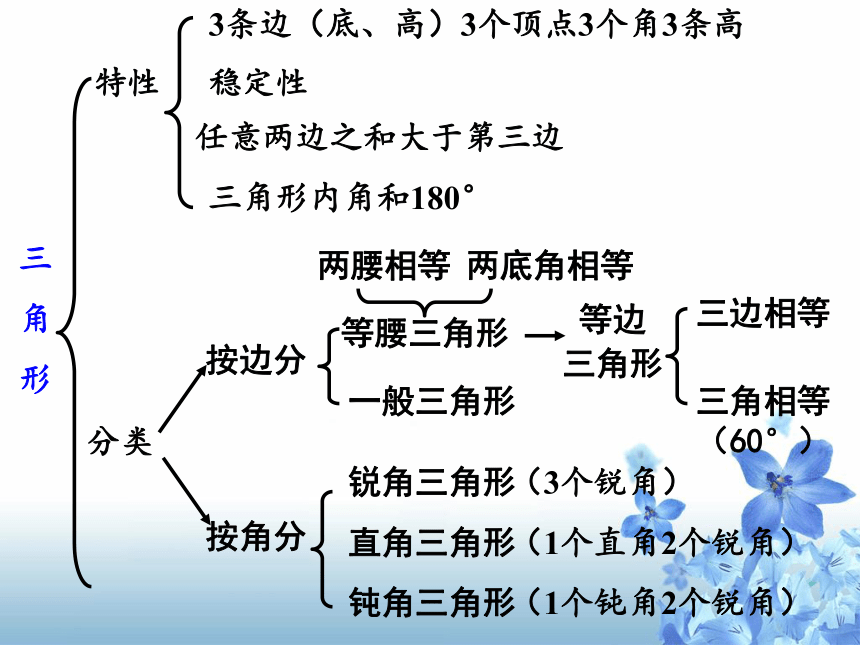
三
角
形
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
等边
三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
3条边(底、高)3个顶点3个角3条高
按边分
锐角三角形
直角三角形
钝角三角形
一般三角形
等腰三角形
按角分
(3个锐角)
(1个直角2个锐角)
(1个钝角2个锐角)
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
3条边(底、高)3个顶点3个角3条高
1端点,不可测量
四边形
正方形
长方形
平行
四边形
梯形
(4条边
4个顶点
4个角
内角和360°)
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
特性:只有一组对边平行、
上底、下底、腰、高【无数条】
对边平行且相等(长、宽)
4个直角
对边平行相等,4条边相等 (边长)
4个直角
对边平行且相等
对角相等
易变形
(底、高【无数条】)
四边形
平行四边形
长方形
正方形
梯 形
我们可以用集合图来表示四边形
之间的关系:
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
特性:对边平行相等,4条边相等(边长),4个直角
特性:对边平行且相等(长、宽),4个直角
(4条边
4个顶点
4个角
内角和360°)
特性:对边平行相等(底、高【无数条】),对角相等、易变形
3条边(底、高)3个顶点3个角3条高
特性:只有一组对边平行、上底、下底、腰、高【无数条】
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
1端点,不可测量
圆形
圆心(o),决定位置
半径(r),连接圆心和圆上任意一点。无数条,决定大小
直径(d)通过圆心,两端在圆上。无数条,决定大小
同圆或等圆中
1直径=2半径
画圆:圆规
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
(曲线)
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
特性:对边平行相等,4条边相等(边长),4个直角
特性:对边平行且相等(长、宽),4个直角
(4条边
4个顶点
4个角
内角和360°)
特性:对边平行相等(底、高【无数条】),对角相等、易变形
3条边(底、高)3个顶点3个角3条高
特性:只有一组对边平行、上底、下底、腰、高【无数条】
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
圆心(o)决定位置
半径(r)连接圆心和圆上任意一点。无数条,决定大小
直径(d)通过圆心,两端在圆上。无数条,决定大小
同圆或等圆中 1直径=2半径
1端点,不可测量
画圆:圆规
谢 谢
图形的认识与测量
—平面图形复面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
线
线段
直线
射线
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面,永不相交
平行线间距离相等
垂直
点到直线
的距离
角
从一点引出两条射线
1个端点,不可测量
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
从一点引出两条射线
1端点,不可测量
角
各部分名称:一个顶点两条边
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
分类:
锐角(<90°)
直角(90°)
钝角(90°<钝角< 180°)
平角(180°)
周角(360°)
1周角=
2平角=
4直角
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
从一点引出两条射线
1端点,不可测量
三
角
形
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
等边
三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
3条边(底、高)3个顶点3个角3条高
按边分
锐角三角形
直角三角形
钝角三角形
一般三角形
等腰三角形
按角分
(3个锐角)
(1个直角2个锐角)
(1个钝角2个锐角)
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
3条边(底、高)3个顶点3个角3条高
1端点,不可测量
四边形
正方形
长方形
平行
四边形
梯形
(4条边
4个顶点
4个角
内角和360°)
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
特性:只有一组对边平行、
上底、下底、腰、高【无数条】
对边平行且相等(长、宽)
4个直角
对边平行相等,4条边相等 (边长)
4个直角
对边平行且相等
对角相等
易变形
(底、高【无数条】)
四边形
平行四边形
长方形
正方形
梯 形
我们可以用集合图来表示四边形
之间的关系:
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
特性:对边平行相等,4条边相等(边长),4个直角
特性:对边平行且相等(长、宽),4个直角
(4条边
4个顶点
4个角
内角和360°)
特性:对边平行相等(底、高【无数条】),对角相等、易变形
3条边(底、高)3个顶点3个角3条高
特性:只有一组对边平行、上底、下底、腰、高【无数条】
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
1端点,不可测量
圆形
圆心(o),决定位置
半径(r),连接圆心和圆上任意一点。无数条,决定大小
直径(d)通过圆心,两端在圆上。无数条,决定大小
同圆或等圆中
1直径=2半径
画圆:圆规
平面图形
线
线段
直线
射线
角
三角形
四边形
圆形
(曲线)
正方形
长方形
平行四边形
梯形
两个端点,可测量
没有端点,不可测量
两条直线
平行
相交
同一平面内,永不相交
平行线间距离相等
垂直
点到直线
的距离
各部分名称:一个顶点两条边
分类:锐角(<90°)直角(90°)钝角(90°<钝角< 180°)平角(180°)周角(360°)
大小:角的两边张开的越大,角越大
角的度量单位:度(°)
用量角器量角
特性
分类
三角形内角和180°
稳定性
任意两边之和大于第三边
按边分
按角分:锐角三角形、直角三角形、钝角三角形
(3锐角) (1直角2锐角)(1钝角2锐角)
一般三角形
等边三角形
从一点引出两条射线
等腰三角形
两腰相等
两底角相等
三边相等
三角相等(60°)
特性:对边平行相等,4条边相等(边长),4个直角
特性:对边平行且相等(长、宽),4个直角
(4条边
4个顶点
4个角
内角和360°)
特性:对边平行相等(底、高【无数条】),对角相等、易变形
3条边(底、高)3个顶点3个角3条高
特性:只有一组对边平行、上底、下底、腰、高【无数条】
等腰梯形(两腰相等两底角相等)、直角梯形(1个直角)
圆心(o)决定位置
半径(r)连接圆心和圆上任意一点。无数条,决定大小
直径(d)通过圆心,两端在圆上。无数条,决定大小
同圆或等圆中 1直径=2半径
1端点,不可测量
画圆:圆规
谢 谢
