3.4 实际问题与一元一次方程(6)行程问题 课件(24张PPT)
文档属性
| 名称 | 3.4 实际问题与一元一次方程(6)行程问题 课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 982.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 08:52:18 | ||
图片预览







文档简介
(共24张PPT)
人教版 七年级上册
3.4实际问题与一元一次方程 (6)
行程问题
教学目标:
1.理解行程问题中行程、速度、时间这些基本量之间关系;
2.能利用列一元一次方程解决行程问题中的相遇、追及问题.
3.引导学生在实际生活的问题中体会数学的价值及乐趣.
教学重点:理解行程情境中的行程、时间、速度概念的含
义和基本数量关系,并能简单应用.
教学难点:在具体的实际问题中如何建立方程模型,并通
过找等量关系正确列出方程.
行程问题
1.基本关系式:_________________
2.基本类型:
画示意图分析题意,分清速度及时间,找等量关系(路程分成几部分).
路程=速度×时间
相遇问题;
追及问题
3.基本分析方法:
新知必备
1.甲的速度是每小时行4千米,则他x小时行 千米.
2.乙3小时走了x千米,则他的速度 .
3.甲每小时行4千米,乙每小时行5千米,则甲、 乙 一
小时共行 千米,y小时共行 千米.
4.某一段路程 x 千米,如果火车以49千米/时的速度驶,
那么火车行完全程需要 小时.
4x
9
9y
练习
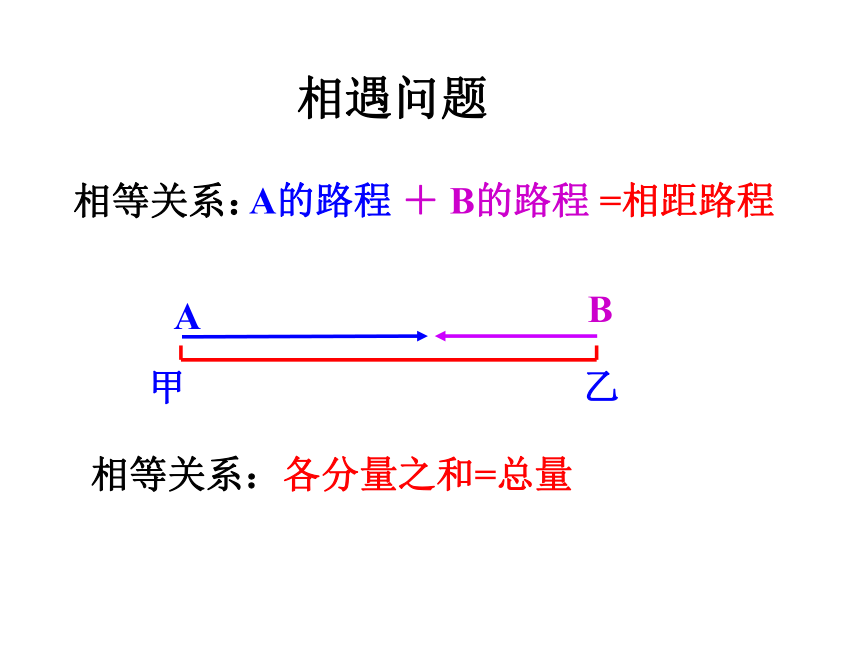
A的路程 + B的路程 =相距路程
相等关系:各分量之和=总量
甲
乙
A
B
相遇问题
相等关系:
1.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
甲
乙
线段图分析:
180千米
45x千米
15x千米
自行车的路程 + 摩托车的路程 =
相等关系:
相距路程
例题解析
1.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
答:经过3小时两人相遇.
解:设经过x小时两人相遇,
则骑自行车的行程为
骑摩托车的行程为
依题意,得
15x+45x=180
解方程,得 x=
3
15x千米,
45x千米,
甲
乙
A
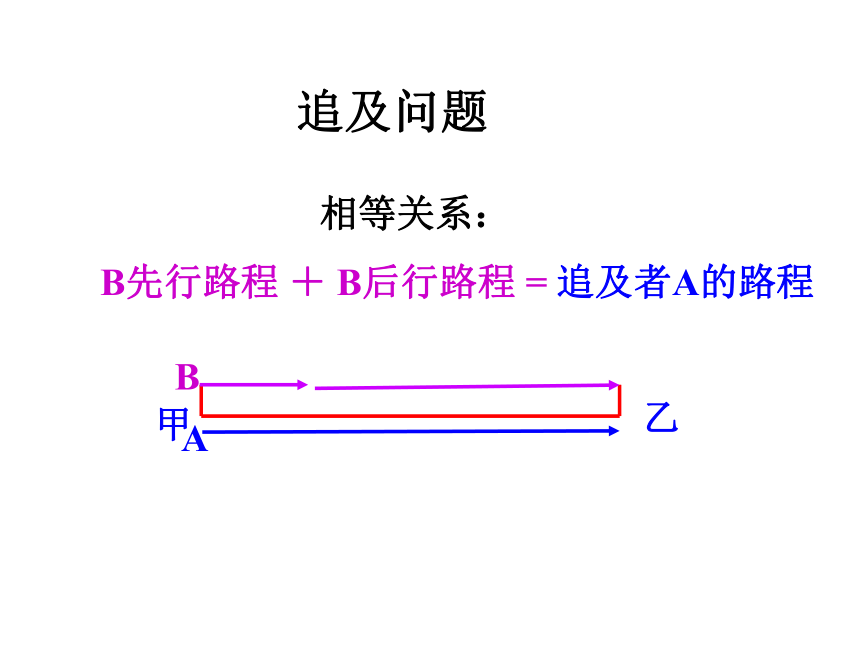
相等关系:
B先行路程 + B后行路程 = 追及者A的路程
B
追及问题
2. 甲、乙两人要从A地到B地,甲骑自行车,以每时走15千米的速度从A地出发走向B地,骑自行车的先出发2小时后,乙才从A地骑摩托车出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,问摩托车经过多少时间追上自行车?
2×15=30千米
15x千米
45x千米
自行车先行路程 + 自行车后行路程
甲
乙
相等关系:
=摩托车的路程
例题解析
2. 甲、乙两人要从A地到B地,甲骑自行车,以每时走15千米的速度从A地出发走向B地,骑自行车的先出发2小时后,乙才从A地骑摩托车出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,问摩托车经过多少时间追上自行车?
答:摩托车经过1小时追上自行车。
解:设摩托车经过x小时追上自行车,
则摩托车的行程为
自行车的行程为
根据题意,得
30+15x=45x
解方程,得 x=
1
45x千米,
(30+15x)千米,
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
例题解析
分 析
(1)反向相遇
相等关系:
叔叔路程 + 小王路程 = 跑道周长
叔叔
小王
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
解:设若两人同时同地反向出发,经过x秒两人首次相遇 ,
则小王跑了
叔叔跑了
根据题意,得
7.5x+5x=400
解方程,得 x=
32
5x米,
7.5x米,
答:若两人同时同地反向出发,经过32秒两人首次相遇 .
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(2)若两人同时同地同向出发,多长时间两人首次相遇?
分 析
(2)同向追及
相等关系:
叔叔路程 -小王路程 = 跑道周长
叔叔
小王
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(2)若两人同时同地同向出发,多长时间两人首次相遇?
解:设若两人同时同地同向出发,经过x秒两人首次相遇 ,
则小王跑了
叔叔跑了
根据题意,得
7.5x-5x=400
解方程,得 x=
160
5x米,
7.5x米,
答:若两人同时同地同向出发,经过160秒两人首次相遇 .
1.一辆卡车从甲地匀速开往乙地,出发2h后,一辆轿车从甲地去追这辆卡车,轿车的速度比卡车的速度快30km/h,但轿车行驶1h后突然出现故障,修理15min后,继续追这辆卡车,此时的速度比原来的速度减小了 ,结果又用了2h才追上这辆卡车,求这辆卡车的速度.
练习巩固
1
3
甲地
乙地
卡车
先走2h
追及地
轿车
1h
2h
15
60
h
+
+
分析
解:设卡车的速度为xkm/h,则轿车的速度为(x+30)km/h,修理后,轿车的速度为(1 - )(x+30)km/h.
1
3
根据题意,得
解方程,得 x=
24
(2+1+ +2)x
15
60
1×(x+30)
+2×(x+30)
(1- )
1
3
答:设卡车的速度为24km/h.
=
整理,得
21
4
x=
x+30 +
4
3
x+40
2.人分别乘速度相同的两辆小汽车同时赶往火车站,每辆车乘4人(包括司机).其中一辆小汽在距离火车站15 千米的地方出现故障,此时距停止检票时间还有42分钟.这时唯一可以利用的交通工具是另一辆小汽车,已知包括司机在内这两辆车各限乘5人,且这两辆车的平均速度都是60千米/时,步行的平均速度都是5千米/时.请设计两种方案,通过计算说明这8人能够在停止检票前赶到火车站.
解:(方案1)
当小汽车出现故障时,乘这辆车的4人下车步行,另一辆车将车内的3人送到火车站后立即返回接步行的4人到火车站.
设乘出现故障汽车的4人步行的距离为x千米,则
解得 x=
所以按这种方案,这8人全部到火车站所需时间为
÷5+(15- )÷60= (小时)=40 (分钟).
由于40 分钟小于42分钟,故此方案可行.
x
5
=
15+15-x
60
30
13
30
13
30
13
35
52
5
13
5
13
(方案2)当小汽车出现故障时,乘这辆车的4人先下车步行,另一辆车将车内的3人送到途中某一位置,让他们下车步行,再立即返回接步行的另外4人,使得两批人员同时到达火车站.
因为第一批人和第二批人到达火车站所用时间相等,所以第一批人步行的距离和第二批人步行的距离相等.
设此距离为y千米,则有
因此这8人全部到火车站所需的时间为
(小时)=37(分钟).
y
5
=
15-2y+15-y
60
解得 y=2.
+
2
5
15-2
60
=
37
60
由于37分钟小于42分钟,故此方案也行.
今天作业
课本P112页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
3.4实际问题与一元一次方程 (6)
行程问题
教学目标:
1.理解行程问题中行程、速度、时间这些基本量之间关系;
2.能利用列一元一次方程解决行程问题中的相遇、追及问题.
3.引导学生在实际生活的问题中体会数学的价值及乐趣.
教学重点:理解行程情境中的行程、时间、速度概念的含
义和基本数量关系,并能简单应用.
教学难点:在具体的实际问题中如何建立方程模型,并通
过找等量关系正确列出方程.
行程问题
1.基本关系式:_________________
2.基本类型:
画示意图分析题意,分清速度及时间,找等量关系(路程分成几部分).
路程=速度×时间
相遇问题;
追及问题
3.基本分析方法:
新知必备
1.甲的速度是每小时行4千米,则他x小时行 千米.
2.乙3小时走了x千米,则他的速度 .
3.甲每小时行4千米,乙每小时行5千米,则甲、 乙 一
小时共行 千米,y小时共行 千米.
4.某一段路程 x 千米,如果火车以49千米/时的速度驶,
那么火车行完全程需要 小时.
4x
9
9y
练习
A的路程 + B的路程 =相距路程
相等关系:各分量之和=总量
甲
乙
A
B
相遇问题
相等关系:
1.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
甲
乙
线段图分析:
180千米
45x千米
15x千米
自行车的路程 + 摩托车的路程 =
相等关系:
相距路程
例题解析
1.甲、乙两地路程为180千米,一人骑自行车从甲地出发每时走15千米,另一人骑摩托车从乙地出发,已知摩托车速度是自行车速度的3倍,若两人同时出发,相向而行,问经过多少时间两人相遇?
答:经过3小时两人相遇.
解:设经过x小时两人相遇,
则骑自行车的行程为
骑摩托车的行程为
依题意,得
15x+45x=180
解方程,得 x=
3
15x千米,
45x千米,
甲
乙
A
相等关系:
B先行路程 + B后行路程 = 追及者A的路程
B
追及问题
2. 甲、乙两人要从A地到B地,甲骑自行车,以每时走15千米的速度从A地出发走向B地,骑自行车的先出发2小时后,乙才从A地骑摩托车出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,问摩托车经过多少时间追上自行车?
2×15=30千米
15x千米
45x千米
自行车先行路程 + 自行车后行路程
甲
乙
相等关系:
=摩托车的路程
例题解析
2. 甲、乙两人要从A地到B地,甲骑自行车,以每时走15千米的速度从A地出发走向B地,骑自行车的先出发2小时后,乙才从A地骑摩托车出发,已知摩托车速度是自行车速度的3倍,若两人同向而行,问摩托车经过多少时间追上自行车?
答:摩托车经过1小时追上自行车。
解:设摩托车经过x小时追上自行车,
则摩托车的行程为
自行车的行程为
根据题意,得
30+15x=45x
解方程,得 x=
1
45x千米,
(30+15x)千米,
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
(2)若两人同时同地同向出发,多长时间两人首次相遇?
例题解析
分 析
(1)反向相遇
相等关系:
叔叔路程 + 小王路程 = 跑道周长
叔叔
小王
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(1)若两人同时同地反向出发,多长时间两人首次相遇?
解:设若两人同时同地反向出发,经过x秒两人首次相遇 ,
则小王跑了
叔叔跑了
根据题意,得
7.5x+5x=400
解方程,得 x=
32
5x米,
7.5x米,
答:若两人同时同地反向出发,经过32秒两人首次相遇 .
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(2)若两人同时同地同向出发,多长时间两人首次相遇?
分 析
(2)同向追及
相等关系:
叔叔路程 -小王路程 = 跑道周长
叔叔
小王
3.小王、叔叔在400米长的环形跑道上练习跑步,小王每秒跑5米,叔叔每秒跑7.5米。
(2)若两人同时同地同向出发,多长时间两人首次相遇?
解:设若两人同时同地同向出发,经过x秒两人首次相遇 ,
则小王跑了
叔叔跑了
根据题意,得
7.5x-5x=400
解方程,得 x=
160
5x米,
7.5x米,
答:若两人同时同地同向出发,经过160秒两人首次相遇 .
1.一辆卡车从甲地匀速开往乙地,出发2h后,一辆轿车从甲地去追这辆卡车,轿车的速度比卡车的速度快30km/h,但轿车行驶1h后突然出现故障,修理15min后,继续追这辆卡车,此时的速度比原来的速度减小了 ,结果又用了2h才追上这辆卡车,求这辆卡车的速度.
练习巩固
1
3
甲地
乙地
卡车
先走2h
追及地
轿车
1h
2h
15
60
h
+
+
分析
解:设卡车的速度为xkm/h,则轿车的速度为(x+30)km/h,修理后,轿车的速度为(1 - )(x+30)km/h.
1
3
根据题意,得
解方程,得 x=
24
(2+1+ +2)x
15
60
1×(x+30)
+2×(x+30)
(1- )
1
3
答:设卡车的速度为24km/h.
=
整理,得
21
4
x=
x+30 +
4
3
x+40
2.人分别乘速度相同的两辆小汽车同时赶往火车站,每辆车乘4人(包括司机).其中一辆小汽在距离火车站15 千米的地方出现故障,此时距停止检票时间还有42分钟.这时唯一可以利用的交通工具是另一辆小汽车,已知包括司机在内这两辆车各限乘5人,且这两辆车的平均速度都是60千米/时,步行的平均速度都是5千米/时.请设计两种方案,通过计算说明这8人能够在停止检票前赶到火车站.
解:(方案1)
当小汽车出现故障时,乘这辆车的4人下车步行,另一辆车将车内的3人送到火车站后立即返回接步行的4人到火车站.
设乘出现故障汽车的4人步行的距离为x千米,则
解得 x=
所以按这种方案,这8人全部到火车站所需时间为
÷5+(15- )÷60= (小时)=40 (分钟).
由于40 分钟小于42分钟,故此方案可行.
x
5
=
15+15-x
60
30
13
30
13
30
13
35
52
5
13
5
13
(方案2)当小汽车出现故障时,乘这辆车的4人先下车步行,另一辆车将车内的3人送到途中某一位置,让他们下车步行,再立即返回接步行的另外4人,使得两批人员同时到达火车站.
因为第一批人和第二批人到达火车站所用时间相等,所以第一批人步行的距离和第二批人步行的距离相等.
设此距离为y千米,则有
因此这8人全部到火车站所需的时间为
(小时)=37(分钟).
y
5
=
15-2y+15-y
60
解得 y=2.
+
2
5
15-2
60
=
37
60
由于37分钟小于42分钟,故此方案也行.
今天作业
课本P112页第5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
