3.4 实际问题与一元一次方程(8)——电话计费问题 课件(共28张PPT)
文档属性
| 名称 | 3.4 实际问题与一元一次方程(8)——电话计费问题 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1002.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 19:37:10 | ||
图片预览








文档简介
(共28张PPT)
人教版 七年级上册
3.4实际问题与一元一次方程 (8)
话费问题
教学目标:
1.能利用列一元一次方程解决生活中简单的收费问题.
2.引导学生在实际生活的问题中体会数学的价值及乐趣.
教学重点:理解收费问题中基本数量关系,并能简单应用.
教学难点:在具体的实际问题中如何建立方程模型,并通
过找等量关系正确列出方程.
某市出租车起步价是8元(3千米及3千米以内为起步价),以后每千米收费是2元,不足1千米按1千米收费,小明乘出租车到达目的地时计价器显示为26元,则此出租车行驶的路程可能为( ).
A.10.5 千米 B.12千米
C.14千米 D.15.5千米
生活中的收费
B
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
例题解析
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
全球通交费=
神州行交费=
50+200×0.1
200×0.3
=70(元)
=60(元)
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
当通话时间为200分时
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
全球通交费=
神州行交费=
50+300×0.1
900×0.3
=80(元)
=90(元)
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
当通话时间为300分时
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
(2)设累计通话x分钟,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元.
因为两种收费一样,
0.3t=50+0.1t
所以
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
解得: x=250.
答:如果一个月内通话250分,那么两种计费方式相同.
(2)设累计通话x分钟,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元.
因为两种收费一样,
0.3t=50+0.1t
所以
全球通 神州行
200分
300分
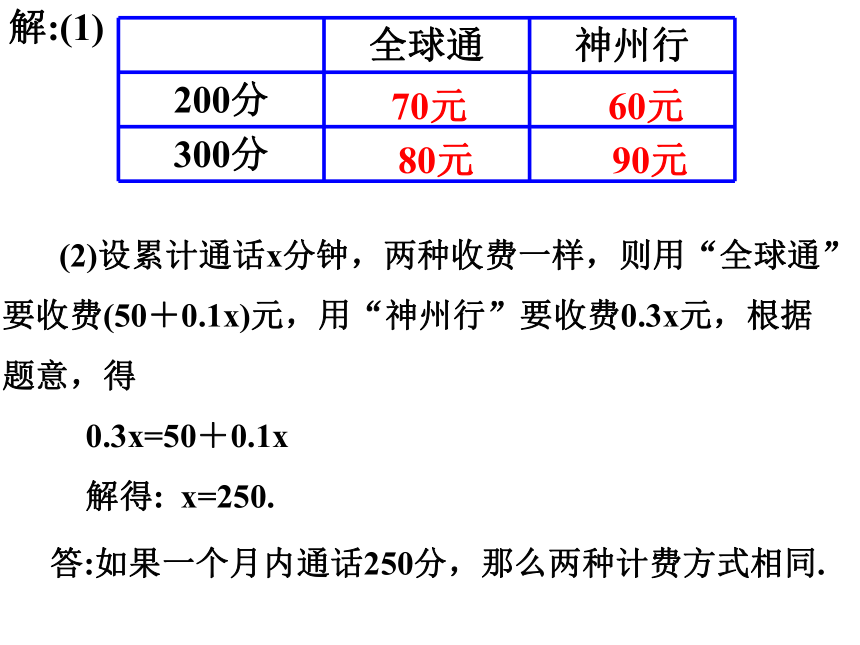
解:(1)
(2)设累计通话x分钟,两种收费一样,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元,根据题意,得
0.3x=50+0.1x
解得: x=250.
答:如果一个月内通话250分,那么两种计费方式相同.
70元
60元
80元
90元
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
问题:什么情况下用“全球通”优惠一些
什么情况下用“神州行”优惠一些
问题探究:
问题1:下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
问题2:话费多少是由什么量决定
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
问题分析
计费方式一
计费方式二
问题3:当使用电话月主叫时间分别是50分、250分、450分时,按方式一和方式二如何计费?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
50
250
450
133
83
107
108
88
88
88
58
88
58
( t 是正整数)
t /分
计费方式一
计费方式二
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且 小于 350
t 等于350
t 大于350
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
问题4:设月主叫时间为t分钟 ,当t在不同时间范围内取值,列表说明按方式 一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
所以当 t =270分时,两种计费方式的费用相等.
问题5:主叫时间多少时,两种方式收费相同?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
问题6:如何根据电话月主叫时间,选择省钱计费方式?
时,选择方式一省钱;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
计费方式一
计费方式二
归纳小结
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法
你有哪些收获?
1.用A4纸在某誊印社复印文件,复印页数不超过20时,每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元. 复印张数为多少时,两处的收费相同?如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
学以致用
复印页数x 誊印社 复印费用/元 图书馆
复印费用/元
x 小于20
x 等于20
x 大于20
解:设复印x张,依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x 恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
0.12x
0.1x
0.1×20=2
0.1x
0.12×20=2.4
2.4+0.09(x-20)
(3)当 x 大于20时,依题意得:
2.4+0.09(x-20)=0.1x 解得: x=60
所以当 x = 60时,两处的收费相同;
当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
综上所述:
当复印量是60张时,两处的收费相同;
当复印量少于60张时,图书馆价格便宜;
当复印量多于60张时,誊印社价格便宜.
2.小明为书房买灯,现在有两种方法可供选择,其中一种是9瓦(即0.009千瓦)的节能灯,售价为49元/盏;另一种是40瓦(即0.04千瓦)的白炽灯,售价为18元/盏.假设两种灯的照明亮度一样,使用寿命都可以达到2800小时,已知小明家所在地的电价是05元/千瓦时.
(1)设照明时间是x小时,请用含有x的式子分别表示用一盏节能灯的费用和一盏白炽灯的费用(注:费用=售价+电费).
(2)小明想在这两种灯中选购一盏:当照明时间多少小时时,两种灯的费用一样多?
解:(1)用一盏节能灯的费用是
49+0.009×0.5x=49 + 0.004 5x(元)
月一盏白炽灯的费用是
18+0.04×0.5x=18+0.02x(元).
(2)根据题意,得
49+0.004 5x=18+0.02x.
解得x=2 000.
所以当照明时间是2000小时时,两种灯的费用一样多.
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体行方案如下表:
每户每月用电数/千瓦时 执行电价/(元/千瓦时) 小于或等于200 0.55 第一档第二档 大于200 小于400 0.6 第三档 大于或等于 400 0.85
例如:一户居民七月份用电420千瓦时,则需缴电费
4200×85=357(元).
某户居民五、六月份共用电500千瓦时,缴电费290.5元已该用户六月份用电量大于五月份,且五、六月份的用电量均小子400千瓦时.问:该户居民五、六月份各用电多少千瓦时
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体行方案如下表:
例如:一户居民七月份用电420千瓦时,则需缴电费
4200×85=357(元).
某户居民五、六月份共用电500千瓦时,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小子400千瓦时.问:该户居民五、六月份各用电多少千瓦时
档次档次
第三档 大于或等于 400
每户每月用电数/千瓦时
执行电价/(元/千瓦时)
档次
第一档
第一档
第一档
小于或等于200
大于200 小于400
0.6
0.85
0.55
解:当五月份用电量为x千瓦时≤200千瓦时,六月份用电(500 - x)千瓦时.由题意,得
0.55x+0.6(500-x)=290.5.
解得x=190
所以六月份用电500-190=310(千瓦时).
当五月份用电量为x千瓦时>200千瓦时,六月份用电量为(500 - x)千瓦时>200千瓦时.由题意,得
0.6x+0.6(500-x)=290.5.
因为此方程无解,所以该情况不符合题意.
答:该户居民五、六月份分别用电190千瓦时、310千瓦时.
今天作业
课本P107页习题3.4第11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教版 七年级上册
3.4实际问题与一元一次方程 (8)
话费问题
教学目标:
1.能利用列一元一次方程解决生活中简单的收费问题.
2.引导学生在实际生活的问题中体会数学的价值及乐趣.
教学重点:理解收费问题中基本数量关系,并能简单应用.
教学难点:在具体的实际问题中如何建立方程模型,并通
过找等量关系正确列出方程.
某市出租车起步价是8元(3千米及3千米以内为起步价),以后每千米收费是2元,不足1千米按1千米收费,小明乘出租车到达目的地时计价器显示为26元,则此出租车行驶的路程可能为( ).
A.10.5 千米 B.12千米
C.14千米 D.15.5千米
生活中的收费
B
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
例题解析
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
全球通交费=
神州行交费=
50+200×0.1
200×0.3
=70(元)
=60(元)
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
当通话时间为200分时
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
全球通交费=
神州行交费=
50+300×0.1
900×0.3
=80(元)
=90(元)
怎么计算交费
交费=月租费+当月通话时间×单价(元/分)
当通话时间为300分时
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
(2)设累计通话x分钟,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元.
因为两种收费一样,
0.3t=50+0.1t
所以
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
解得: x=250.
答:如果一个月内通话250分,那么两种计费方式相同.
(2)设累计通话x分钟,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元.
因为两种收费一样,
0.3t=50+0.1t
所以
全球通 神州行
200分
300分
解:(1)
(2)设累计通话x分钟,两种收费一样,则用“全球通”要收费(50+0.1x)元,用“神州行”要收费0.3x元,根据题意,得
0.3x=50+0.1x
解得: x=250.
答:如果一个月内通话250分,那么两种计费方式相同.
70元
60元
80元
90元
两种移动电话计费方式表如下:
全球通 神州行
月租费 50元/月 0
本地通话费 0.10元/分 0.30元/分
(1)一个月内在本地通话200分和300分,按两种计费方式 各须交费多少元
(2)对于某个本地通话时间,会出现两种计费方式的收费一样的情况吗
问题:什么情况下用“全球通”优惠一些
什么情况下用“神州行”优惠一些
问题探究:
问题1:下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
问题2:话费多少是由什么量决定
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
问题分析
计费方式一
计费方式二
问题3:当使用电话月主叫时间分别是50分、250分、450分时,按方式一和方式二如何计费?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
50
250
450
133
83
107
108
88
88
88
58
88
58
( t 是正整数)
t /分
计费方式一
计费方式二
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且 小于 350
t 等于350
t 大于350
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)
=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
问题4:设月主叫时间为t分钟 ,当t在不同时间范围内取值,列表说明按方式 一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
所以当 t =270分时,两种计费方式的费用相等.
问题5:主叫时间多少时,两种方式收费相同?
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
350
0
150
108
88
58
88
( t 是正整数)
t /分
88
88
?
270
问题6:如何根据电话月主叫时间,选择省钱计费方式?
时,选择方式一省钱;
时,选择方式二省钱.
t 小于 270分
t 大于 270分
计费方式一
计费方式二
归纳小结
请回顾电话计费问题的探究过程,并回答以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法
你有哪些收获?
1.用A4纸在某誊印社复印文件,复印页数不超过20时,每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元. 复印张数为多少时,两处的收费相同?如何根据复印的页数选择复印的地点使总价格比较便宜?(复印的页数不为零)
学以致用
复印页数x 誊印社 复印费用/元 图书馆
复印费用/元
x 小于20
x 等于20
x 大于20
解:设复印x张,依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x 恒成立,
图书馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
0.12x
0.1x
0.1×20=2
0.1x
0.12×20=2.4
2.4+0.09(x-20)
(3)当 x 大于20时,依题意得:
2.4+0.09(x-20)=0.1x 解得: x=60
所以当 x = 60时,两处的收费相同;
当x大于20且小于60时,图书馆价格便宜;
当x大于60时,誊印社价格便宜.
综上所述:
当复印量是60张时,两处的收费相同;
当复印量少于60张时,图书馆价格便宜;
当复印量多于60张时,誊印社价格便宜.
2.小明为书房买灯,现在有两种方法可供选择,其中一种是9瓦(即0.009千瓦)的节能灯,售价为49元/盏;另一种是40瓦(即0.04千瓦)的白炽灯,售价为18元/盏.假设两种灯的照明亮度一样,使用寿命都可以达到2800小时,已知小明家所在地的电价是05元/千瓦时.
(1)设照明时间是x小时,请用含有x的式子分别表示用一盏节能灯的费用和一盏白炽灯的费用(注:费用=售价+电费).
(2)小明想在这两种灯中选购一盏:当照明时间多少小时时,两种灯的费用一样多?
解:(1)用一盏节能灯的费用是
49+0.009×0.5x=49 + 0.004 5x(元)
月一盏白炽灯的费用是
18+0.04×0.5x=18+0.02x(元).
(2)根据题意,得
49+0.004 5x=18+0.02x.
解得x=2 000.
所以当照明时间是2000小时时,两种灯的费用一样多.
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体行方案如下表:
每户每月用电数/千瓦时 执行电价/(元/千瓦时) 小于或等于200 0.55 第一档第二档 大于200 小于400 0.6 第三档 大于或等于 400 0.85
例如:一户居民七月份用电420千瓦时,则需缴电费
4200×85=357(元).
某户居民五、六月份共用电500千瓦时,缴电费290.5元已该用户六月份用电量大于五月份,且五、六月份的用电量均小子400千瓦时.问:该户居民五、六月份各用电多少千瓦时
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体行方案如下表:
例如:一户居民七月份用电420千瓦时,则需缴电费
4200×85=357(元).
某户居民五、六月份共用电500千瓦时,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小子400千瓦时.问:该户居民五、六月份各用电多少千瓦时
档次档次
第三档 大于或等于 400
每户每月用电数/千瓦时
执行电价/(元/千瓦时)
档次
第一档
第一档
第一档
小于或等于200
大于200 小于400
0.6
0.85
0.55
解:当五月份用电量为x千瓦时≤200千瓦时,六月份用电(500 - x)千瓦时.由题意,得
0.55x+0.6(500-x)=290.5.
解得x=190
所以六月份用电500-190=310(千瓦时).
当五月份用电量为x千瓦时>200千瓦时,六月份用电量为(500 - x)千瓦时>200千瓦时.由题意,得
0.6x+0.6(500-x)=290.5.
因为此方程无解,所以该情况不符合题意.
答:该户居民五、六月份分别用电190千瓦时、310千瓦时.
今天作业
课本P107页习题3.4第11、12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
