河北省张家口市桥东区2022-2023学年七年级(上)数学期末模拟测试(含答案及详解)
文档属性
| 名称 | 河北省张家口市桥东区2022-2023学年七年级(上)数学期末模拟测试(含答案及详解) |

|
|
| 格式 | zip | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览




文档简介
张家口市桥东区2022-2023学年七年级(上)数学期末模拟测试
一、选择题(本题共16个小题,1~10小题各3分;11~16小题各2分,共 42分。下列各题,每小题只有一个选项符合题意。)
1. -3的倒数是( )
A. B. C. D.
2. 如图所示,由A到B有①、②、③三条路线,最短的路线选①的理由是( )
A. 两点确定一条直线 B. 两点间距离的定义
C. 两点之间,线段最短 D. 因为它直
3. 一个整数815550…0用科学记数法表示为8.1555×1010,则原数中“0”的个数为( )
A. 4 B. 6 C. 7 D. 10
4. 下列方程是一元一次方程的是( )
A. x2=6 B. =1
C. 2x-5y=2 D. 5x-1=7
5. 某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对应的面上的汉字是( )
A. 礼 B. 赞
C. 百 D. 年
6. 如图,OA是点O北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是( )
A. 北偏西30°
B. 北偏西60°
C. 东偏北30°
D. 东偏北60°
7. 如果,则x的值是( )
A B. C. D.
8. 若a,b是互为相反数(a≠0),则关于x的一元一次方程ax+b=0的解是( )
A. 1 B. ﹣1 C. ﹣1或1 D. 任意有理数
9. 已知关于的方程的解是,则的值为( )
A. B. C. D.
10. 《九章算术》中记载一问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 设有x人,则表示物价的代数式可以是( )
A. B.
C. D.
11. 《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.设城中有户人家,可列方程为( )
A. B.
C. D.
12. 如图,已知线段,M是中点,点N在上,,那么线段的长为( )
A. B. C. D.
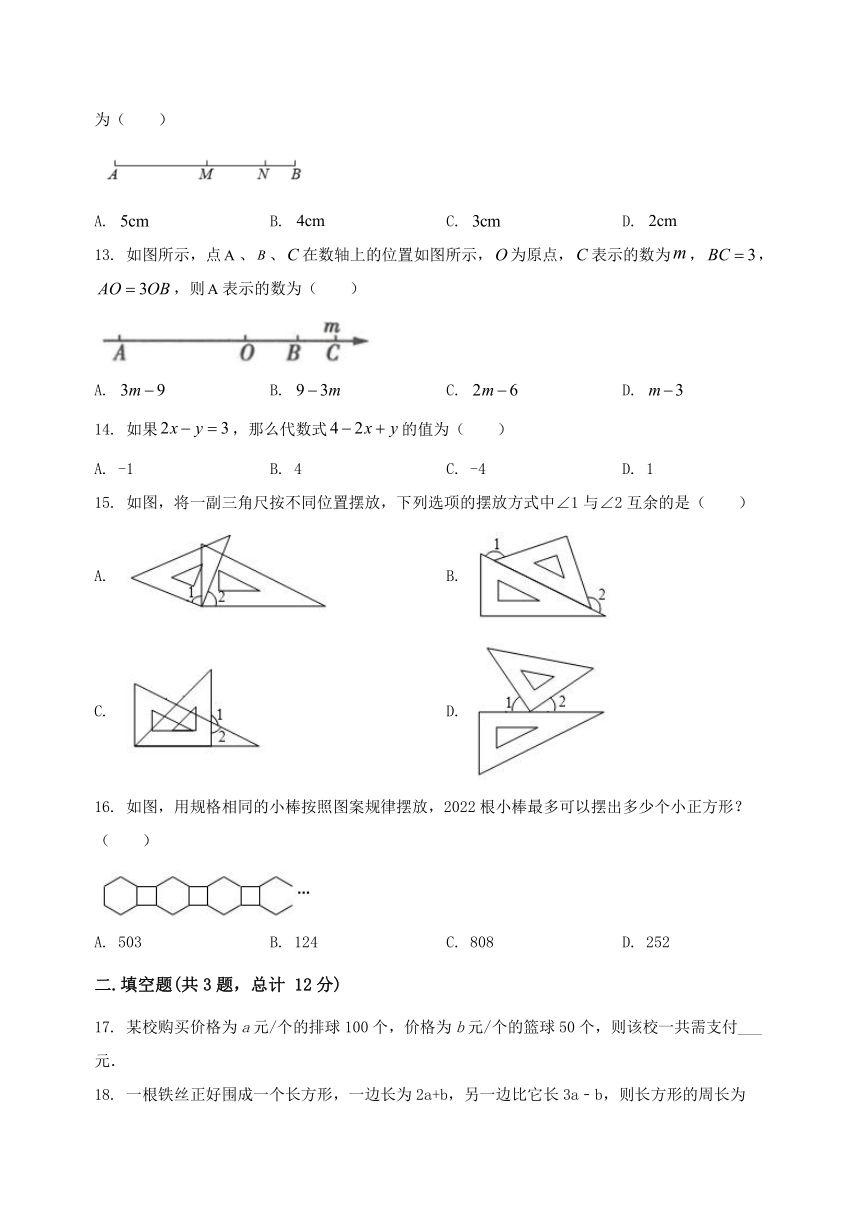
13. 如图所示,点、、在数轴上的位置如图所示,为原点,表示的数为,,,则表示的数为( )
A. B. C. D.
14. 如果,那么代数式的值为( )
A. -1 B. 4 C. -4 D. 1
15. 如图,将一副三角尺按不同位置摆放,下列选项的摆放方式中∠1与∠2互余的是( )
A. B.
C. D.
16. 如图,用规格相同的小棒按照图案规律摆放,2022根小棒最多可以摆出多少个小正方形?( )
A. 503 B. 124 C. 808 D. 252
二.填空题(共3题,总计 12分)
17. 某校购买价格为a元/个的排球100个,价格为b元/个的篮球50个,则该校一共需支付___元.
18. 一根铁丝正好围成一个长方形,一边长为2a+b,另一边比它长3a﹣b,则长方形的周长为______.
19. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马_______天追上慢马.
三.解答题(共7题,总计66分)
20. (1);
(2).
21. 解方程
(1)
(2)
22. 先化简,再求值:.其中
23. 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
24. 如图,已知的补角等于它的余角的10倍.
(1)求的度数;
(2)若平分,,求的度数.
25. 如图,数轴的原点O表示学校的位置,超市位于学校正西600m的点A处,小明家位于学校正东200m的点B处,小明与妈妈在该超市购物后,同时从超市出发,沿AB步行回家,两人的速度大小保持不变.小明先把部分物品送到家,当小明妈妈行至点C处时,小明刚好到家并立即沿原路返回,帮妈妈拿余下的物品.已知小明妈妈每分钟走60m.
(1)小明每分钟走多少米?
(2)两人于何处再次相遇?
(3)从出发到再次相遇,多少分钟时两人相距100m?
26. 如图1,已知线段,点M是线段上一点,点C在线段上,点D在线段上,C、D两点分别从M、B出发以的速度沿直线运动,运动方向如箭头所示,其中a、b满足条件:.
(1)直接写出:____________,_____________;
(2)若,当点C、D运动了,求的值;
(3)如图2,若,点N是直线上一点,且,求与的数量关系.
张家口市桥东区2022-2023学年七年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:∵,
∴的倒数是.
故选C
2.【答案】:C
【解析】:解:由A到B有①、②、③三条路线,最短的路线选①的理由是:
两点之间,线段最短.
故选C
3.【答案】:B
【解析】:∵8.1555×1010表示原数为81555000000,
∴原数中“0”的个数为6,
故选B.
4.【答案】:D
【解析】:A、不是一元一次方程,故本选项不符合题意;
B、=1该方程不是整式方程,是分式方程,故本选项不符合题意;
C、该方程中含有2个未知数,是二元一次方程,故本选项不符合题意;
D、符合一元一次方程的定义,故本选项符合题意;
故选:D.
5.【答案】:D
【解析】:结合展开图可知:建对应百;党对应年;赞对应礼,
故答案为:D.
6.【答案】:B
【解析】:因为射线OA和OB垂直,
所以∠AOB=90°.
因为∠AOC=30°,
所以∠BOC=90°-30°=60°,
所以OB的方位角是北偏西60°.
故选:B.
7.【答案】:C
【解析】:解:∵,
∴x=±4,
故选C.
8.【答案】:A
【解析】:∵a,b互为相反数
∴
∵ax+b=0
∴
∴
故选:A
9.【答案】:A
【解析】:解:把x=3代入方程
得3m+2=3,
解得:m=,
故选:A.
10.【答案】:A
【解析】:设有x人,由题意可表示物价的代数式是或,
故选A.
11.【答案】:D
【解析】:解:设城中有x户人家,
依题意,得:.
故选:D
12.【答案】:C
【解析】:解:∵cm,M是AB中点,
∴cm,
又∵cm,
∴cm.
故选C.
13.【答案】:B
【解析】:由表示,,可得表示的数为,
又,可得,
又在原点左侧,可得表示的数为.
故选:B.
14.【答案】:D
【解析】:解:已知
=4-(2x-y)=4-3=1.
故选D.
15.【答案】:D
【解析】:解:A.∵∠1+∠2度数不确定,
∴∠1与∠2不互为余角,故错误;
B.∵∠1+45°+∠2+45°=180°+180°=360°,
∴∠1+∠2=270°,
即∠1与∠2不互为余角,故错误;
C.∵∠1+∠2=180°,
∴∠1与∠2不互为余角,故错误;
D.∵∠1+∠2+90°=180°,
∴∠1+∠2=90°,
即∠1与∠2互为余角,故正确.
故选:D.
16.【答案】:D
【解析】:解:出现1个正六边形和1个小正方形时,需要小棒的根数是9根;
出现2个正六边形和2个小正方形时,需要小棒的根数是17根;
出现3个正六边形和3个小正方形时,需要小棒的根数是25根;
…,
则出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根;
(2022-1)÷8=252……5,
故选:D.
【点睛】本题主要考查图形的变化规律,根据图案的变化归纳出出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根是解题的关键.
二. 填空题
17.【答案】:
【解析】:解:由题意得:
该校一共需支付元,
故答案为:.
18.【答案】: 14a+2b
【解析】:∵长方形的一边长为2a+b,另一边比它长3a﹣b,
∴另一边为2a+b+3a﹣b=5a,
∴长方形的周长为2(2a+b+5a)=14a+2b
【点睛】此题主要考查整式的加减,解题的关键是熟知整式的加减运算法则.
19.【答案】: 20
【解析】:解:设快马行x天追上慢马,则此时慢马行了(x+12)日,
依题意,得:240x=150(x+12),
解得:x=20,
∴快马20天追上慢马,
故答案为:20.
三.解答题
20【答案】:
(1)-91
(2)
【解析】:
【小问1详解】
原式
=-91;
【小问2详解】
原式
=-1.
【点睛】本题主要考查了有理数的混合运算,熟练掌握运算法则以及运算律是解此题的关键.
21【答案】:
(1)
(2)
【解析】:
(1)先移项,再合并同类项,最后系数化为1,即可求解;
(2)先去分母,再去括号,然后移项,合并同类项,最后系数化为1,即可求解.
【小问1详解】
解:,
移项,得:,
合并同类项,得:,
系数化为1,得:.
【小问2详解】
解:,
去分母(两边同乘4),得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:.
22【答案】:
;.
【解析】:
解:
当时,
原式
.
23【答案】:
安排10人生产螺钉,12人生产螺母
【解析】:
解:设分配x名工人生产螺母,则(22﹣x)人生产螺钉,由题意得:
2000x=2×1200(22﹣x),解得:x=12,则22﹣x=10.
答:应安排10人生产螺钉,12名工人生产螺母.
24【答案】:
(1)的度数为
(2)
【解析】:
【小问1详解】
解:设,
由题意得:,
解得.
∴的度数为.
【小问2详解】
解:设,则,
∵平分,
∴ ,
由题意,,
解得,
∴;
故的度数为136°.
25【答案】:
(1)小明每分钟走100米;
两人于学校(点O处)再次相遇;
(3)或分钟时两人相距100m.
【解析】:
解:(1)[200﹣(﹣600)]÷[(﹣120+600)÷60]=100(米).
故小明每分钟走100米;
(2)因为[200﹣(﹣120)]÷(100+60)=2(分钟),
2×60+(﹣120)=0.
故两人于学校(点O处)再次相遇;
(3)设从出发到再次相遇,x分钟时两人相距100m,分两种情况:
①小明到家前,依题意有
100x﹣60x=100,
解得x=;
②小明到家后,依题意有
100x+60x+100=800×2,
解得x=.
故从出发到再次相遇,或分钟时两人相距100m.
【点睛】本题考查了数轴和一元一次方程的应用,解题关键是理解数轴是表示数的意义,理清数量关系,列出方程.
26【答案】:
(1)1,3 (2)8cm
(3)或
【解析】:
(1)根据绝对值的非负性得出a-1=0,b-3=0,求解即可;
(2)当C、D运动时,,,结合图形求解即可;
(3)分两种情况:当点N在线段上时;当点N在线段的延长线上时;利用线段间的数量关系求解即可.
【小问1详解】
解:∵|a 1|+|b 3|=0
∴a-1=0,b-3=0,
∴a=1,b=3,
故答案为:1;3;
【小问2详解】
当C、D运动时,,,
∴.
【小问3详解】
当点N在线段上时,
∵,
又∵,
∴,
∴.
当点N在线段的延长线上时,
∵,
又∵,
∴.
综上所述,或.
【点睛】题目主要考查绝对值的非负性及点的运动,线段间的数量关系等,理解题意,根据图象得出线段间的数量关系是解题关键.
一、选择题(本题共16个小题,1~10小题各3分;11~16小题各2分,共 42分。下列各题,每小题只有一个选项符合题意。)
1. -3的倒数是( )
A. B. C. D.
2. 如图所示,由A到B有①、②、③三条路线,最短的路线选①的理由是( )
A. 两点确定一条直线 B. 两点间距离的定义
C. 两点之间,线段最短 D. 因为它直
3. 一个整数815550…0用科学记数法表示为8.1555×1010,则原数中“0”的个数为( )
A. 4 B. 6 C. 7 D. 10
4. 下列方程是一元一次方程的是( )
A. x2=6 B. =1
C. 2x-5y=2 D. 5x-1=7
5. 某班数学老师结合中国共产党建党一百周年,在班级内组织了一堂“正方体展开图猜猜看”活动课,下图是该正方体展开图的一种,那么原正方体中,与“党”字所在面对应的面上的汉字是( )
A. 礼 B. 赞
C. 百 D. 年
6. 如图,OA是点O北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是( )
A. 北偏西30°
B. 北偏西60°
C. 东偏北30°
D. 东偏北60°
7. 如果,则x的值是( )
A B. C. D.
8. 若a,b是互为相反数(a≠0),则关于x的一元一次方程ax+b=0的解是( )
A. 1 B. ﹣1 C. ﹣1或1 D. 任意有理数
9. 已知关于的方程的解是,则的值为( )
A. B. C. D.
10. 《九章算术》中记载一问题:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 设有x人,则表示物价的代数式可以是( )
A. B.
C. D.
11. 《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽.问:城中家几何?大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完.设城中有户人家,可列方程为( )
A. B.
C. D.
12. 如图,已知线段,M是中点,点N在上,,那么线段的长为( )
A. B. C. D.
13. 如图所示,点、、在数轴上的位置如图所示,为原点,表示的数为,,,则表示的数为( )
A. B. C. D.
14. 如果,那么代数式的值为( )
A. -1 B. 4 C. -4 D. 1
15. 如图,将一副三角尺按不同位置摆放,下列选项的摆放方式中∠1与∠2互余的是( )
A. B.
C. D.
16. 如图,用规格相同的小棒按照图案规律摆放,2022根小棒最多可以摆出多少个小正方形?( )
A. 503 B. 124 C. 808 D. 252
二.填空题(共3题,总计 12分)
17. 某校购买价格为a元/个的排球100个,价格为b元/个的篮球50个,则该校一共需支付___元.
18. 一根铁丝正好围成一个长方形,一边长为2a+b,另一边比它长3a﹣b,则长方形的周长为______.
19. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马_______天追上慢马.
三.解答题(共7题,总计66分)
20. (1);
(2).
21. 解方程
(1)
(2)
22. 先化简,再求值:.其中
23. 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
24. 如图,已知的补角等于它的余角的10倍.
(1)求的度数;
(2)若平分,,求的度数.
25. 如图,数轴的原点O表示学校的位置,超市位于学校正西600m的点A处,小明家位于学校正东200m的点B处,小明与妈妈在该超市购物后,同时从超市出发,沿AB步行回家,两人的速度大小保持不变.小明先把部分物品送到家,当小明妈妈行至点C处时,小明刚好到家并立即沿原路返回,帮妈妈拿余下的物品.已知小明妈妈每分钟走60m.
(1)小明每分钟走多少米?
(2)两人于何处再次相遇?
(3)从出发到再次相遇,多少分钟时两人相距100m?
26. 如图1,已知线段,点M是线段上一点,点C在线段上,点D在线段上,C、D两点分别从M、B出发以的速度沿直线运动,运动方向如箭头所示,其中a、b满足条件:.
(1)直接写出:____________,_____________;
(2)若,当点C、D运动了,求的值;
(3)如图2,若,点N是直线上一点,且,求与的数量关系.
张家口市桥东区2022-2023学年七年级(上)数学期末模拟测试
参考答案及解析
一.选择题
1.【答案】:C
【解析】:解:∵,
∴的倒数是.
故选C
2.【答案】:C
【解析】:解:由A到B有①、②、③三条路线,最短的路线选①的理由是:
两点之间,线段最短.
故选C
3.【答案】:B
【解析】:∵8.1555×1010表示原数为81555000000,
∴原数中“0”的个数为6,
故选B.
4.【答案】:D
【解析】:A、不是一元一次方程,故本选项不符合题意;
B、=1该方程不是整式方程,是分式方程,故本选项不符合题意;
C、该方程中含有2个未知数,是二元一次方程,故本选项不符合题意;
D、符合一元一次方程的定义,故本选项符合题意;
故选:D.
5.【答案】:D
【解析】:结合展开图可知:建对应百;党对应年;赞对应礼,
故答案为:D.
6.【答案】:B
【解析】:因为射线OA和OB垂直,
所以∠AOB=90°.
因为∠AOC=30°,
所以∠BOC=90°-30°=60°,
所以OB的方位角是北偏西60°.
故选:B.
7.【答案】:C
【解析】:解:∵,
∴x=±4,
故选C.
8.【答案】:A
【解析】:∵a,b互为相反数
∴
∵ax+b=0
∴
∴
故选:A
9.【答案】:A
【解析】:解:把x=3代入方程
得3m+2=3,
解得:m=,
故选:A.
10.【答案】:A
【解析】:设有x人,由题意可表示物价的代数式是或,
故选A.
11.【答案】:D
【解析】:解:设城中有x户人家,
依题意,得:.
故选:D
12.【答案】:C
【解析】:解:∵cm,M是AB中点,
∴cm,
又∵cm,
∴cm.
故选C.
13.【答案】:B
【解析】:由表示,,可得表示的数为,
又,可得,
又在原点左侧,可得表示的数为.
故选:B.
14.【答案】:D
【解析】:解:已知
=4-(2x-y)=4-3=1.
故选D.
15.【答案】:D
【解析】:解:A.∵∠1+∠2度数不确定,
∴∠1与∠2不互为余角,故错误;
B.∵∠1+45°+∠2+45°=180°+180°=360°,
∴∠1+∠2=270°,
即∠1与∠2不互为余角,故错误;
C.∵∠1+∠2=180°,
∴∠1与∠2不互为余角,故错误;
D.∵∠1+∠2+90°=180°,
∴∠1+∠2=90°,
即∠1与∠2互为余角,故正确.
故选:D.
16.【答案】:D
【解析】:解:出现1个正六边形和1个小正方形时,需要小棒的根数是9根;
出现2个正六边形和2个小正方形时,需要小棒的根数是17根;
出现3个正六边形和3个小正方形时,需要小棒的根数是25根;
…,
则出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根;
(2022-1)÷8=252……5,
故选:D.
【点睛】本题主要考查图形的变化规律,根据图案的变化归纳出出现n个正六边形和n个小正方形时,需要小棒的根数是(8n+1)根是解题的关键.
二. 填空题
17.【答案】:
【解析】:解:由题意得:
该校一共需支付元,
故答案为:.
18.【答案】: 14a+2b
【解析】:∵长方形的一边长为2a+b,另一边比它长3a﹣b,
∴另一边为2a+b+3a﹣b=5a,
∴长方形的周长为2(2a+b+5a)=14a+2b
【点睛】此题主要考查整式的加减,解题的关键是熟知整式的加减运算法则.
19.【答案】: 20
【解析】:解:设快马行x天追上慢马,则此时慢马行了(x+12)日,
依题意,得:240x=150(x+12),
解得:x=20,
∴快马20天追上慢马,
故答案为:20.
三.解答题
20【答案】:
(1)-91
(2)
【解析】:
【小问1详解】
原式
=-91;
【小问2详解】
原式
=-1.
【点睛】本题主要考查了有理数的混合运算,熟练掌握运算法则以及运算律是解此题的关键.
21【答案】:
(1)
(2)
【解析】:
(1)先移项,再合并同类项,最后系数化为1,即可求解;
(2)先去分母,再去括号,然后移项,合并同类项,最后系数化为1,即可求解.
【小问1详解】
解:,
移项,得:,
合并同类项,得:,
系数化为1,得:.
【小问2详解】
解:,
去分母(两边同乘4),得:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:.
22【答案】:
;.
【解析】:
解:
当时,
原式
.
23【答案】:
安排10人生产螺钉,12人生产螺母
【解析】:
解:设分配x名工人生产螺母,则(22﹣x)人生产螺钉,由题意得:
2000x=2×1200(22﹣x),解得:x=12,则22﹣x=10.
答:应安排10人生产螺钉,12名工人生产螺母.
24【答案】:
(1)的度数为
(2)
【解析】:
【小问1详解】
解:设,
由题意得:,
解得.
∴的度数为.
【小问2详解】
解:设,则,
∵平分,
∴ ,
由题意,,
解得,
∴;
故的度数为136°.
25【答案】:
(1)小明每分钟走100米;
两人于学校(点O处)再次相遇;
(3)或分钟时两人相距100m.
【解析】:
解:(1)[200﹣(﹣600)]÷[(﹣120+600)÷60]=100(米).
故小明每分钟走100米;
(2)因为[200﹣(﹣120)]÷(100+60)=2(分钟),
2×60+(﹣120)=0.
故两人于学校(点O处)再次相遇;
(3)设从出发到再次相遇,x分钟时两人相距100m,分两种情况:
①小明到家前,依题意有
100x﹣60x=100,
解得x=;
②小明到家后,依题意有
100x+60x+100=800×2,
解得x=.
故从出发到再次相遇,或分钟时两人相距100m.
【点睛】本题考查了数轴和一元一次方程的应用,解题关键是理解数轴是表示数的意义,理清数量关系,列出方程.
26【答案】:
(1)1,3 (2)8cm
(3)或
【解析】:
(1)根据绝对值的非负性得出a-1=0,b-3=0,求解即可;
(2)当C、D运动时,,,结合图形求解即可;
(3)分两种情况:当点N在线段上时;当点N在线段的延长线上时;利用线段间的数量关系求解即可.
【小问1详解】
解:∵|a 1|+|b 3|=0
∴a-1=0,b-3=0,
∴a=1,b=3,
故答案为:1;3;
【小问2详解】
当C、D运动时,,,
∴.
【小问3详解】
当点N在线段上时,
∵,
又∵,
∴,
∴.
当点N在线段的延长线上时,
∵,
又∵,
∴.
综上所述,或.
【点睛】题目主要考查绝对值的非负性及点的运动,线段间的数量关系等,理解题意,根据图象得出线段间的数量关系是解题关键.
同课章节目录
