4.3 相似多边形 课件(28张PPT)
文档属性
| 名称 | 4.3 相似多边形 课件(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.3 相似多边形
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握相似多边形的概念,熟悉相似比的定义;
2、学会判定两个图形是否是相似多边形;
3、掌握相似多边形的性质,并学会用相似多边形的性质来进行有关的实际计算;
导入新课
观察与思考
想一想:下面的图形有什么相同点和不同点
讲授新课
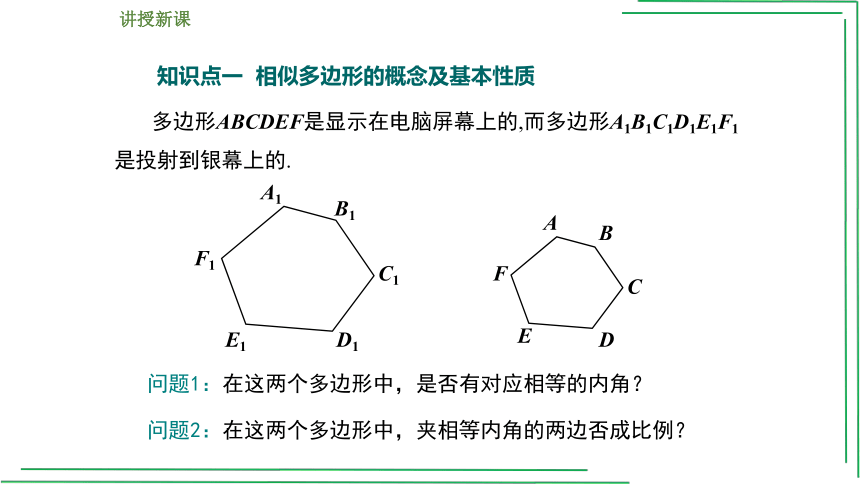
知识点一 相似多边形的概念及基本性质
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
问题1:在这两个多边形中,是否有对应相等的内角?
问题2:在这两个多边形中,夹相等内角的两边否成比例?
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
各角分别相等、各边成比例的两个多边形叫做相
似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
归纳总结
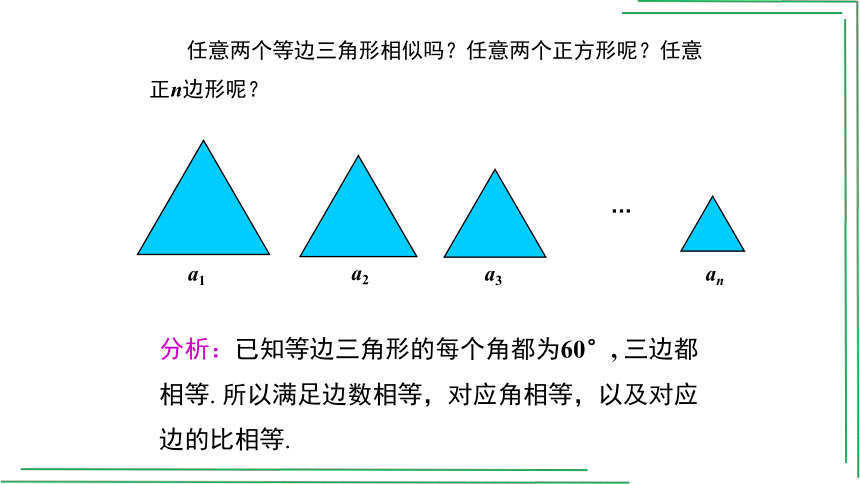
任意两个等边三角形相似吗?任意两个正方形呢?任意正n边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
…
同理,任意两个正方形都相似.
归纳:任意两个边数相等正多边形都相似.
a1
a2
a3
an
问题:任意的两个菱形是否形似?
典例精析
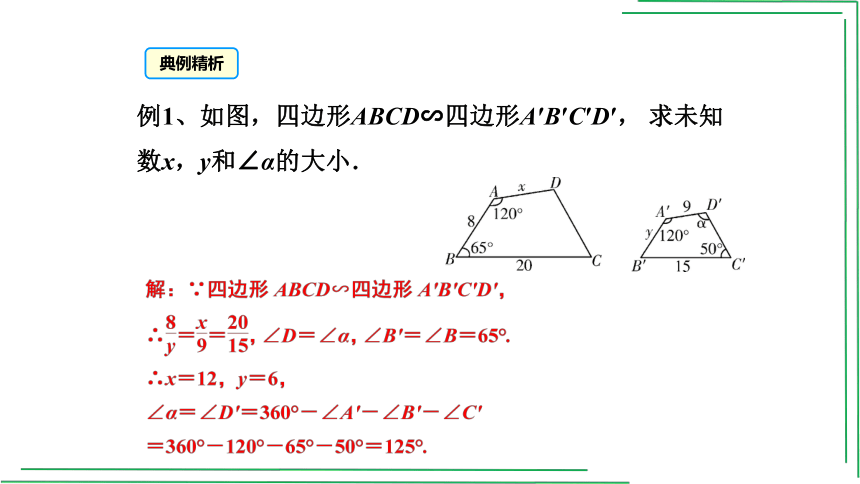
例1、如图,四边形ABCD∽四边形A′B′C′D′, 求未知数x,y和∠α的大小.
练一练
1.如图,E,F分别是矩形ABCD的边BC,AD的中点,若矩形ABEF与矩形ABCD相似,AB=4,求AD的长.
解:设 AD=BC=x,则AF= x
∵矩形ABEF∽矩形BCDA
∴ ∴
∴x=
∴AD=
知识点二 相似多边形的应用
例:如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴ .
∴EF2=AD·BC=3×4=12,
∴EF=2 .
∵四边形AEFD∽四边形EBCF,
∴AE:EB=AD:EF=3:2 = :2.
A
B
C
D
E
F
当堂练习
课堂小结
1.相似多边形的性质
对应角相等,对应边的比相等
几何语言
∵
∴
相似图形对应边的比叫做相似比,记作k.
四边形ABCD∽四边形A'B'C'D'
∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D'
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.3 相似多边形
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握相似多边形的概念,熟悉相似比的定义;
2、学会判定两个图形是否是相似多边形;
3、掌握相似多边形的性质,并学会用相似多边形的性质来进行有关的实际计算;
导入新课
观察与思考
想一想:下面的图形有什么相同点和不同点
讲授新课
知识点一 相似多边形的概念及基本性质
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
问题1:在这两个多边形中,是否有对应相等的内角?
问题2:在这两个多边形中,夹相等内角的两边否成比例?
多边形ABCDEF是显示在电脑屏幕上的,而多边形A1B1C1D1E1F1是投射到银幕上的.
各角分别相等、各边成比例的两个多边形叫做相
似多边形.
相似多边形的对应边的比叫作相似比.
相似多边形的对应角相等,对应边成比例.
相似比:
相似多边形的特征:
相似多边形的定义:
归纳总结
任意两个等边三角形相似吗?任意两个正方形呢?任意正n边形呢?
a1
a2
a3
an
…
分析:已知等边三角形的每个角都为60°, 三边都相等. 所以满足边数相等,对应角相等,以及对应边的比相等.
…
同理,任意两个正方形都相似.
归纳:任意两个边数相等正多边形都相似.
a1
a2
a3
an
问题:任意的两个菱形是否形似?
典例精析
例1、如图,四边形ABCD∽四边形A′B′C′D′, 求未知数x,y和∠α的大小.
练一练
1.如图,E,F分别是矩形ABCD的边BC,AD的中点,若矩形ABEF与矩形ABCD相似,AB=4,求AD的长.
解:设 AD=BC=x,则AF= x
∵矩形ABEF∽矩形BCDA
∴ ∴
∴x=
∴AD=
知识点二 相似多边形的应用
例:如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
解:∵四边形AEFD∽四边形EBCF,
∴ .
∴EF2=AD·BC=3×4=12,
∴EF=2 .
∵四边形AEFD∽四边形EBCF,
∴AE:EB=AD:EF=3:2 = :2.
A
B
C
D
E
F
当堂练习
课堂小结
1.相似多边形的性质
对应角相等,对应边的比相等
几何语言
∵
∴
相似图形对应边的比叫做相似比,记作k.
四边形ABCD∽四边形A'B'C'D'
∠A=∠A',∠B=∠B',∠C=∠C',∠D=∠D'
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
