4.4 探索三角形相似的条件 课件(61张PPT)
文档属性
| 名称 | 4.4 探索三角形相似的条件 课件(61张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 00:00:00 | ||
图片预览





文档简介
(共61张PPT)
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.4 探索三角形相似的条件
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握利用两角分别相等的两个三角形相似;
2、熟练掌握利用两边对应成比例且夹角相等的两个三角形相似;
3、掌握三边成比例的两个三角形相似;
导入新课
温故知新
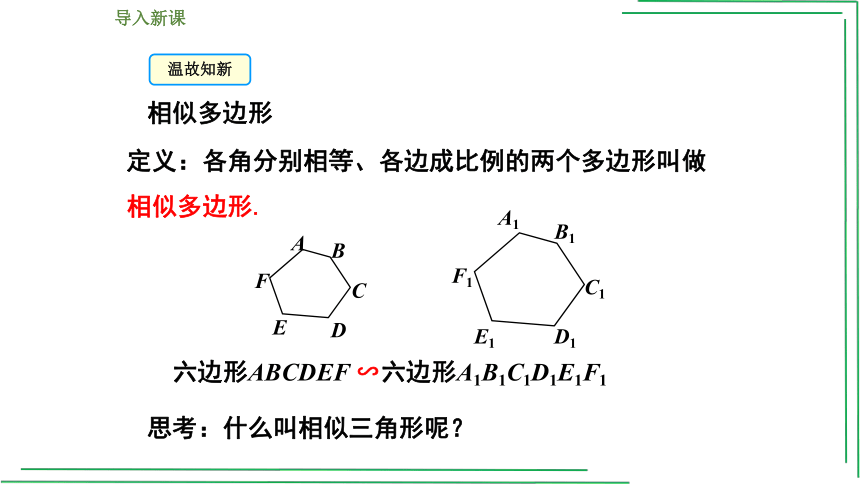
相似多边形
定义:各角分别相等、各边成比例的两个多边形叫做相似多边形.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
六边形ABCDEF ∽六边形A1B1C1D1E1F1
思考:什么叫相似三角形呢?
观察教师的一个三角板(有30°,60°的角),这两个三角板的外围的三角形的三个内角有什么关系 这些三角形相似吗
讲授新课
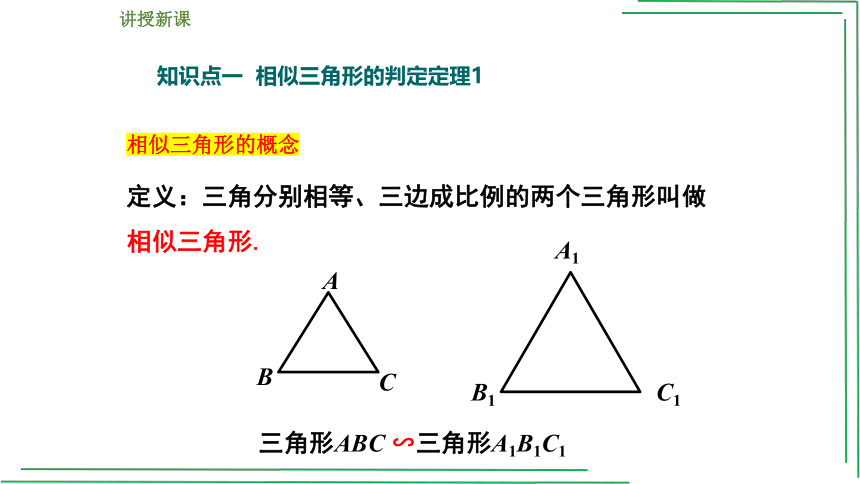
知识点一 相似三角形的判定定理1
定义:三角分别相等、三边成比例的两个三角形叫做相似三角形.
三角形ABC ∽三角形A1B1C1
A
B
C
A1
B1
C1
相似三角形的概念
思考:两个三角形至少满足什么条件就相似呢?类比两个三角形全等的条件,寻找判定两个相似的条件?
A
B
C
A1
B1
C1
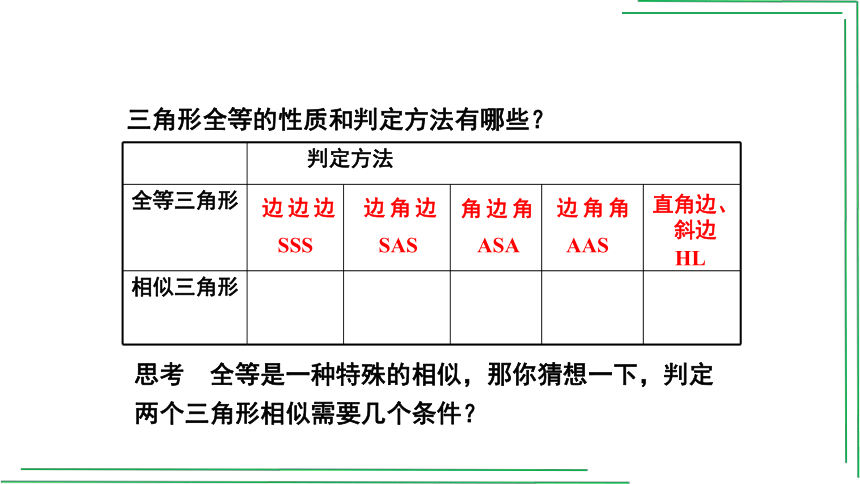
判定方法 全等三角形
相似三角形
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
HL
三角形全等的性质和判定方法有哪些?
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
直角边、斜边
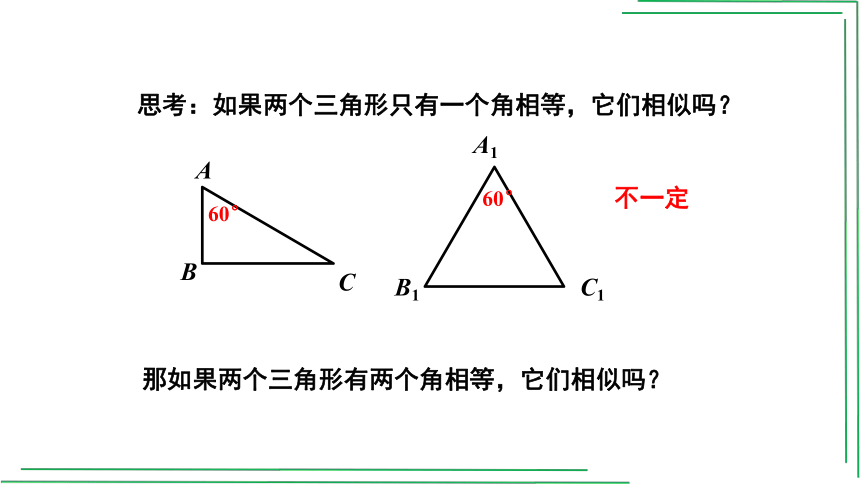
思考:如果两个三角形只有一个角相等,它们相似吗?
A
B
C
A1
B1
C1
不一定
那如果两个三角形有两个角相等,它们相似吗?
60°
60°
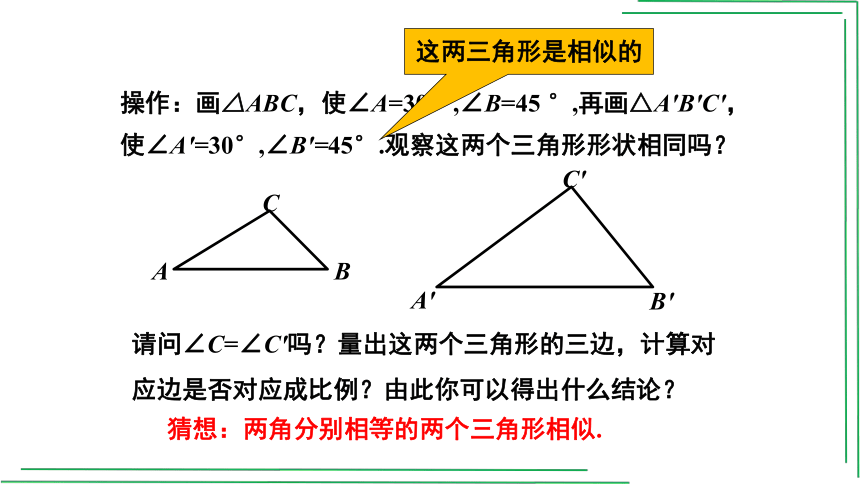
操作:画△ABC,使∠A=30°,∠B=45 °,再画△A′B′C′,使∠A′=30°,∠B′=45°.观察这两个三角形形状相同吗?
A
B
C
A′
B′
C′
请问∠C=∠C′吗?量出这两个三角形的三边,计算对应边是否对应成比例?由此你可以得出什么结论?
这两三角形是相似的
猜想:两角分别相等的两个三角形相似.
已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
B’
A’
D
E
C’
B
A
C
证明:两角分别相等的两个三角形相似
典例精析
证明:在△A′B′C′的边A′B′、A′C′上,分
别截取A′D=AB,A′E=AC,连接DE.
∵A′D=AB,∠A=∠A′,A′E=AC,
∴△A′DE≌△ABC,
∴∠A′DE=∠B,
又∵∠B′=∠B,
∴∠A′DE=∠B′,
∴DE∥B′C′,
B’
A’
D
E
C’
B
A
C
【例1】已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
过D连接DF// A′C′
∵ DF// A′C′ ,DE∥B′C′
∴四边形EDFC′是平行四边形
∴DE=FC′,
∵
∴△A′DE∽△A′B′C′,
∴△A′B′C′∽△ABC.
B
A
C
B’
A’
D
E
C’
F
两角分别相等的两个三角形相似.
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形的判定定理:
注意:对应点写在对应的位置.
1.如图,△ABC中,DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解: ∵ DE∥BC,EF∥AB.
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似.)
练一练
知识点二 相似三角形的判定定理2
问题1.有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?∠C′=∠C吗?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?
我发现这两个三角形是相似的
画一画
猜想:两边成比例夹角相等的两个三角形相似.
已知:在△ABC与△A′B′C′中,∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∠ADE= ∠B′, ∠A ′ ED= ∠C′
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B’
A’
D
E
C’
两边成比例夹角相等的两个三角形相似.
典例精析
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
【例2】已知:在△ABC与△A′B′C′中,∠A= ∠A′,
求证:△A′B′C′∽△ABC.
如果△ABC与△A'B'C'两边成比例,且其中一边
所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
知识拓展
3
3
C
C
60°
)
4
A
B
)
C′
1.5
B′
2
60°
A′
判定定理2:
两边成比例且夹角相等的两个三角形相似
探究相似三角形的条件
用数学符号表示:
∵ ∠A=∠A',
∴ ΔABC ∽ ΔA'B'C'
练一练
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC(两边成比例且夹角相等的两个三角形相似)
∴ ∴BC=3. ∴DE=
1.如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
2.如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
解: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴△ABC∽△DEF.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
知识点三 三角形相似的判定3
思考:类比全等三角形的判定方法,还有其他判定两个三角形相似的方法吗?
两个三角形的三边成比例,那么这两个三角形一定相似吗?
A
B
C
A1
B1
C1
操作:画△ ABC 与△A1B1C1,使
(1)比较∠A与∠A1的大小, △ ABC 与△A1B1C1相似吗?
A
B
C
A1
B1
C1
(2)改变k值的大小, △ ABC 与△A1B1C1还相似吗?
猜想:三边成比例的两个三角形相似
A
B
C
A1
B1
C1
求证:三边成比例的两个三角形相似
已知:在△ ABC 与△A1B1C1中,
求证:△ ABC ∽ △A1B1C1
典例精析
证明:在△A1B1C1的边A1B1 (或延长线)上截取 A1D=AB,
过点D作DE∥B1C1交A1C1于点E.
∵ DE∥B1C1 ,
∴△ADE∽△A1B1C1.
A
B
C
A1
B1
C1
D
E
【例3】已知:在△ ABC 与△A1B1C1中,
求证:△ ABC ∽ △A1B1C1
∴
又
∴
∴
∴
(SSS)
∵
∴
A
B
C
A1
B1
C1
D
E
三边成比例的两个三角形相似
相似三角形的判定定理3:
用数学符号表示:
∴ △ ABC ∽ △A1B1C1
∵
A
B
C
A1
B1
C1
判定三角形相似的方法:
如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应
(注意:大对大,小对小,中对中)
总结归纳
练一练
1.如图,小方格的边长为1 ,△ ABC与△ A′B′C′相似吗
C
B
A
A′
B′
C′
解: △ ABC∽△ A′B′C′
小结:先求边,然后排序,最后作比.
2.如图,在△ABC和△ADE中, ∠BAD=20°,求∠CAE的度数.
解:∵
∴△ABC∽△ADE
∴∠BAC=∠DAE.
∴∠BAC - ∠DAC =∠DAE-∠DAC.
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
A
B
C
D
E
知识点四 黄金分割
如图,点 C 把线段 AB 分成两条线段 AC 和 BC
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割
点 C 叫做线段 AB 的黄金分割点
AC 与 AB 的比叫做黄金比.
C
A
B
(AC2=AB BC)
AC
BC
AC
AB
=
(
)
计算黄金比.
解:由 ,得AC2 = AB·BC.
设AB = 1,AC = x,则BC = 1 – x.
∴ x2 = 1 ×(1 - x).
即 x2 + x – 1 = 0.
解方程得:x1= x2=
黄金比
≈
0.618 : 1
AC
AB
AC
BC
=
C
A
B
2.如图,已知线段AB按照如下方法作图:
1.经过点B作BD⊥AB,使BD= AB
2.连接AD,在AD上截取DE=DB.
3.在AB上截取AC=AE.
思考:点C是线段AB的黄金分割点吗
A
B
D
E
C
黄金分割点的画法
AC
AB
AC
BC
=
即求 = :1
A
B
D
E
C
解:设BD = x ,AB = 2x,
在Rt △ABD中,由勾股定理,得
∴ AD = x
DE= x , AE= x –x=
AC=
AC
AB
=
2x
=
练一练
1.在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
当堂练习
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
利用两边及夹角判定三角形相似
定理2:两边对应成比例且夹角相等的两个三角形相似
相似三角形的判定定理2的运用
利用三边判定三角形相似
定理:三边对应成比例的两个三角形相似
相似三角形的判定定理3的运用
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.4 探索三角形相似的条件
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握利用两角分别相等的两个三角形相似;
2、熟练掌握利用两边对应成比例且夹角相等的两个三角形相似;
3、掌握三边成比例的两个三角形相似;
导入新课
温故知新
相似多边形
定义:各角分别相等、各边成比例的两个多边形叫做相似多边形.
A1
B1
C1
D1
E1
F1
A
B
C
D
E
F
六边形ABCDEF ∽六边形A1B1C1D1E1F1
思考:什么叫相似三角形呢?
观察教师的一个三角板(有30°,60°的角),这两个三角板的外围的三角形的三个内角有什么关系 这些三角形相似吗
讲授新课
知识点一 相似三角形的判定定理1
定义:三角分别相等、三边成比例的两个三角形叫做相似三角形.
三角形ABC ∽三角形A1B1C1
A
B
C
A1
B1
C1
相似三角形的概念
思考:两个三角形至少满足什么条件就相似呢?类比两个三角形全等的条件,寻找判定两个相似的条件?
A
B
C
A1
B1
C1
判定方法 全等三角形
相似三角形
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
HL
三角形全等的性质和判定方法有哪些?
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
直角边、斜边
思考:如果两个三角形只有一个角相等,它们相似吗?
A
B
C
A1
B1
C1
不一定
那如果两个三角形有两个角相等,它们相似吗?
60°
60°
操作:画△ABC,使∠A=30°,∠B=45 °,再画△A′B′C′,使∠A′=30°,∠B′=45°.观察这两个三角形形状相同吗?
A
B
C
A′
B′
C′
请问∠C=∠C′吗?量出这两个三角形的三边,计算对应边是否对应成比例?由此你可以得出什么结论?
这两三角形是相似的
猜想:两角分别相等的两个三角形相似.
已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
B’
A’
D
E
C’
B
A
C
证明:两角分别相等的两个三角形相似
典例精析
证明:在△A′B′C′的边A′B′、A′C′上,分
别截取A′D=AB,A′E=AC,连接DE.
∵A′D=AB,∠A=∠A′,A′E=AC,
∴△A′DE≌△ABC,
∴∠A′DE=∠B,
又∵∠B′=∠B,
∴∠A′DE=∠B′,
∴DE∥B′C′,
B’
A’
D
E
C’
B
A
C
【例1】已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
过D连接DF// A′C′
∵ DF// A′C′ ,DE∥B′C′
∴四边形EDFC′是平行四边形
∴DE=FC′,
∵
∴△A′DE∽△A′B′C′,
∴△A′B′C′∽△ABC.
B
A
C
B’
A’
D
E
C’
F
两角分别相等的两个三角形相似.
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形的判定定理:
注意:对应点写在对应的位置.
1.如图,△ABC中,DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解: ∵ DE∥BC,EF∥AB.
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似.)
练一练
知识点二 相似三角形的判定定理2
问题1.有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
问题2.类比三角形全等的判定方法(SAS,SSS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
相似
①任意画△ABC;
②再画△A′B′C′,使∠A′=∠A,且
③量出B′C′及BC的长,计算 的值,并比较是否三边都对应成比例?
④量出∠B与∠B′的度数,∠B′=∠B吗?∠C′=∠C吗?
⑤由上面的画图,你能发现△A′B′C′与△ABC有何关系?
我发现这两个三角形是相似的
画一画
猜想:两边成比例夹角相等的两个三角形相似.
已知:在△ABC与△A′B′C′中,∠A= ∠A′,
证明:在△A′B′C′的边A′B′上截取点D,使A′D=AB.过点D作DE∥B′C′,交A′C′于点E.
∵DE∥B′C′,
∠ADE= ∠B′, ∠A ′ ED= ∠C′
∴△A′DE∽△A′B′C′.
求证:△A′B′C′∽△ABC.
B
A
C
B’
A’
D
E
C’
两边成比例夹角相等的两个三角形相似.
典例精析
∵A′D=AB,
∴A′E=AC.
又∠A′=∠A.
∴△A′DE≌△ABC,
∴△A′B′C′∽△ABC.
B
A
C
D
E
B'
A'
C'
【例2】已知:在△ABC与△A′B′C′中,∠A= ∠A′,
求证:△A′B′C′∽△ABC.
如果△ABC与△A'B'C'两边成比例,且其中一边
所对的角相等,那么这两个三角形一定相似吗?由此你能得到什么结论?
知识拓展
3
3
C
C
60°
)
4
A
B
)
C′
1.5
B′
2
60°
A′
判定定理2:
两边成比例且夹角相等的两个三角形相似
探究相似三角形的条件
用数学符号表示:
∵ ∠A=∠A',
∴ ΔABC ∽ ΔA'B'C'
练一练
解:∵AE=1.5,AC=2,
∴
∵ ∴
又∵∠EAD=∠CAB,
∴△ADE∽△ABC(两边成比例且夹角相等的两个三角形相似)
∴ ∴BC=3. ∴DE=
1.如图所示,D,E分别是△ABC的边AC,AB上的点,
AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
C
B
E
D
2.如图,在 △ABC 中,CD是边AB上的高,且 求证:∠ACB=90°.
A
B
C
D
解: ∵ CD是边AB上的高,
∴ ∠ADC= ∠CDB=90°.
∴△ABC∽△DEF.
∴ ∠ACD= ∠B.
∴ ∠ACB= ∠ACD+ ∠BCD= ∠B+ ∠BCD= 90°.
知识点三 三角形相似的判定3
思考:类比全等三角形的判定方法,还有其他判定两个三角形相似的方法吗?
两个三角形的三边成比例,那么这两个三角形一定相似吗?
A
B
C
A1
B1
C1
操作:画△ ABC 与△A1B1C1,使
(1)比较∠A与∠A1的大小, △ ABC 与△A1B1C1相似吗?
A
B
C
A1
B1
C1
(2)改变k值的大小, △ ABC 与△A1B1C1还相似吗?
猜想:三边成比例的两个三角形相似
A
B
C
A1
B1
C1
求证:三边成比例的两个三角形相似
已知:在△ ABC 与△A1B1C1中,
求证:△ ABC ∽ △A1B1C1
典例精析
证明:在△A1B1C1的边A1B1 (或延长线)上截取 A1D=AB,
过点D作DE∥B1C1交A1C1于点E.
∵ DE∥B1C1 ,
∴△ADE∽△A1B1C1.
A
B
C
A1
B1
C1
D
E
【例3】已知:在△ ABC 与△A1B1C1中,
求证:△ ABC ∽ △A1B1C1
∴
又
∴
∴
∴
(SSS)
∵
∴
A
B
C
A1
B1
C1
D
E
三边成比例的两个三角形相似
相似三角形的判定定理3:
用数学符号表示:
∴ △ ABC ∽ △A1B1C1
∵
A
B
C
A1
B1
C1
判定三角形相似的方法:
如果题中给出了两个三角形的三边的长,分别算出三条对应边的比值,看是否相等,计算时最长边与最长边对应,最短边与最短边对应
(注意:大对大,小对小,中对中)
总结归纳
练一练
1.如图,小方格的边长为1 ,△ ABC与△ A′B′C′相似吗
C
B
A
A′
B′
C′
解: △ ABC∽△ A′B′C′
小结:先求边,然后排序,最后作比.
2.如图,在△ABC和△ADE中, ∠BAD=20°,求∠CAE的度数.
解:∵
∴△ABC∽△ADE
∴∠BAC=∠DAE.
∴∠BAC - ∠DAC =∠DAE-∠DAC.
即 ∠BAD=∠CAE.
∵∠BAD=20°,
∴∠CAE=20°.
A
B
C
D
E
知识点四 黄金分割
如图,点 C 把线段 AB 分成两条线段 AC 和 BC
如果
AC
AB
AC
BC
=
那么称线段 AB 被点 C 黄金分割
点 C 叫做线段 AB 的黄金分割点
AC 与 AB 的比叫做黄金比.
C
A
B
(AC2=AB BC)
AC
BC
AC
AB
=
(
)
计算黄金比.
解:由 ,得AC2 = AB·BC.
设AB = 1,AC = x,则BC = 1 – x.
∴ x2 = 1 ×(1 - x).
即 x2 + x – 1 = 0.
解方程得:x1= x2=
黄金比
≈
0.618 : 1
AC
AB
AC
BC
=
C
A
B
2.如图,已知线段AB按照如下方法作图:
1.经过点B作BD⊥AB,使BD= AB
2.连接AD,在AD上截取DE=DB.
3.在AB上截取AC=AE.
思考:点C是线段AB的黄金分割点吗
A
B
D
E
C
黄金分割点的画法
AC
AB
AC
BC
=
即求 = :1
A
B
D
E
C
解:设BD = x ,AB = 2x,
在Rt △ABD中,由勾股定理,得
∴ AD = x
DE= x , AE= x –x=
AC=
AC
AB
=
2x
=
练一练
1.在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
解:设肚脐到脚底的距离为 x m,根据题意,得
,解得x = 0.96.
设穿上 y m高的高跟鞋看起来会更美,则
解得 y≈0.075,而0.075m=7.5cm.
故她应该穿约为7.5cm高的高跟鞋看起来会更美.
当堂练习
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
利用两边及夹角判定三角形相似
定理2:两边对应成比例且夹角相等的两个三角形相似
相似三角形的判定定理2的运用
利用三边判定三角形相似
定理:三边对应成比例的两个三角形相似
相似三角形的判定定理3的运用
黄金分割
点C把线段AB分成两条线段AC和BC,如果 , 那么称线段AB被点C黄金分割.点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
黄金分割点:一条线段有两个黄金分割点
黄金比:较长线段:原线段 =
定义
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
