4.6 利用相似三角形测高 课件(40张PPT)
文档属性
| 名称 | 4.6 利用相似三角形测高 课件(40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 08:27:11 | ||
图片预览








文档简介
(共40张PPT)
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.6 利用相似三角形测高
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、通过测量旗杆高度学会相似三角形的实际应用,复习巩固相似三角形的相关知识点;
2、可以灵活运用相似三角形的性质解决实际问题;
导入新课
温故知新
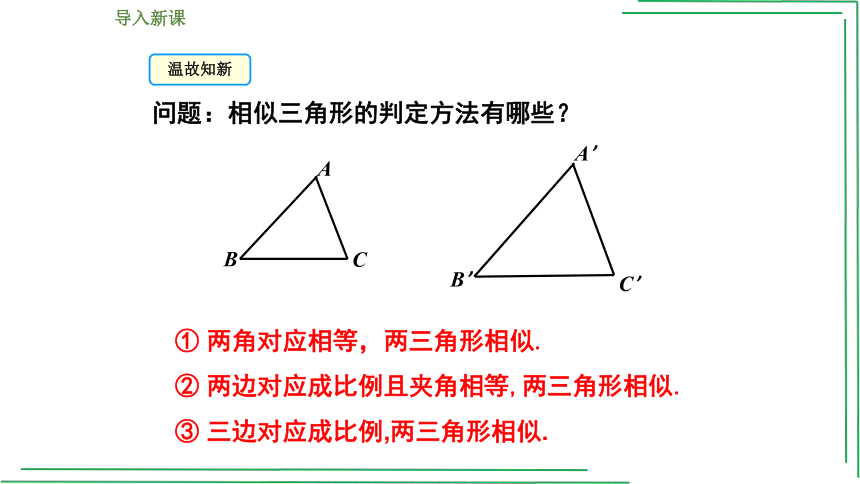
问题:相似三角形的判定方法有哪些?
① 两角对应相等,两三角形相似.
② 两边对应成比例且夹角相等,两三角形相似.
③ 三边对应成比例,两三角形相似.
B’
A’
C’
B
A
C
观察与思考
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗?
探究活动:利用相似三角形的有关知识测量旗杆的高度
活动工具:小镜子、标杆、皮尺等测量工具
活动方式:分组活动、全班交流研讨
讲授新课
知识点一 运用相似三角形解决高度(长度)问题
例1:如下图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
解:∵BF∥ED,∴∠BAO=∠EDF,
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴ = ,∴ = ,
∴BO=134.
因此金字塔高134 m.
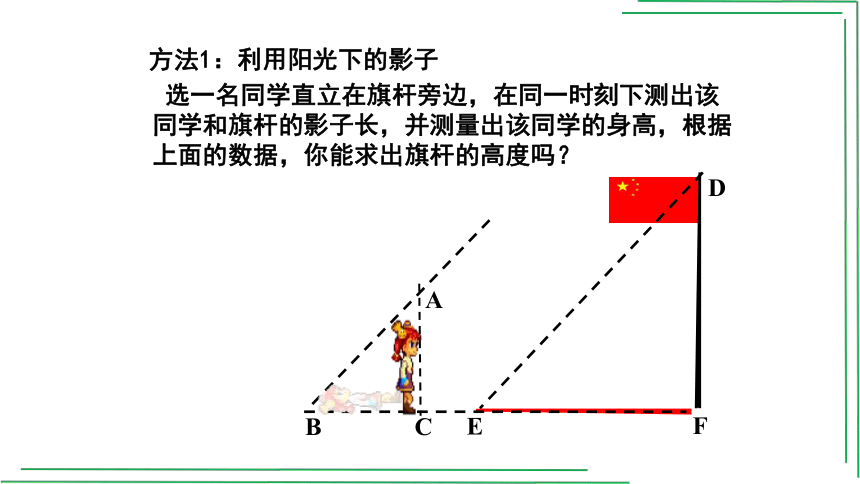
方法1:利用阳光下的影子
选一名同学直立在旗杆旁边,在同一时刻下测出该同学和旗杆的影子长,并测量出该同学的身高,根据上面的数据,你能求出旗杆的高度吗?
D
F
E
A
B
C
A
B
C
D
E
F
A
D
F
E
B
C
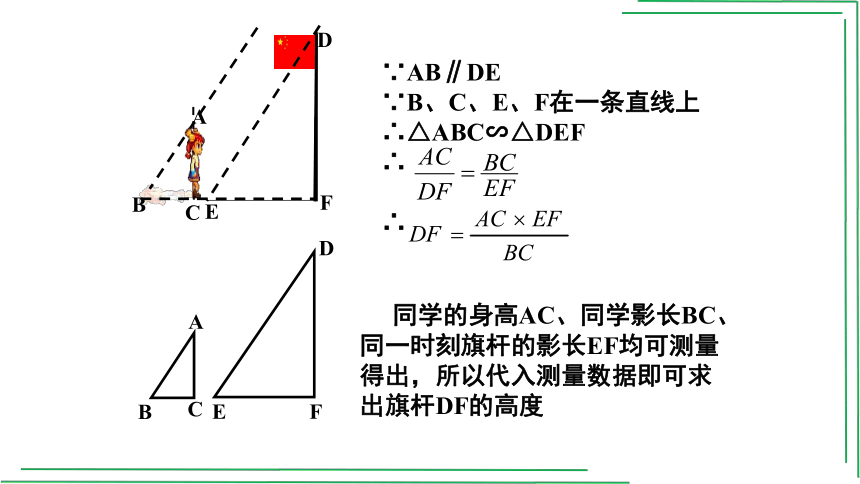
∵AB∥DE
∵B、C、E、F在一条直线上
∴△ABC∽△DEF
∴
∴
同学的身高AC、同学影长BC、同一时刻旗杆的影长EF均可测量得出,所以代入测量数据即可求出旗杆DF的高度
物1高 :物2高 = 影1长 :影2长
测高方法一:利用阳光下的影子
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
归纳总结
测量数据:身高AC、影长BC、旗杆影长EF.
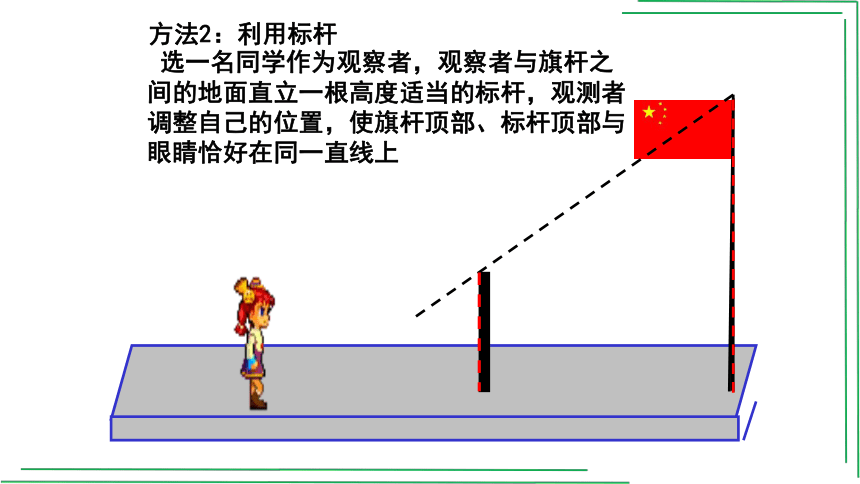
方法2:利用标杆
选一名同学作为观察者,观察者与旗杆之间的地面直立一根高度适当的标杆,观测者调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在同一直线上
方法2:利用标杆
测出观察者的脚到旗杆的距离,及到标杆的距离,观察者眼睛到地面的高度,标杆的高,你能求出旗杆的高吗?
C
E
B
F
D
3
M
N
1
2
A
需要测量的数据:
人与标杆的距离AM
人与旗杆的距离AN
标杆的高度EF
人眼到地面的距离AB
过A作AN⊥CD交DC于点N,交EF于M
∵EF∥CN
∴△AME∽△ANC
A
B
C
D
E
F
M
N
∴
∴
∵四边形ABDN为矩形
∴DN=AB
∴CD=CN+DN
方法2:利用标杆
C
E
B
F
A
D
构造相似:△AME∽△ANC.
找比例:AM:AN=EM:CN
M
N
需要测量的数据:
人与标杆的距离AM
人与旗杆的距离AN
标杆的高度EF
方法3:利用镜子反射
A
C
D
E
B
平面镜
操作:1.选一名学生作为观测者,在他与旗杆之间的地面上平放一面镜子,固定镜子的位置;
2.观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,
方法3:利用镜子反射
A
C
D
E
B
平面镜
3.测出观察者的脚与镜子的距离BE、
旗杆底部与镜子的距离DE、
观察者的眼睛到地面的高度AB
那么能求出旗杆的高度吗?
A
C
D
E
B
平面镜
方法3:利用镜子反射
A
C
D
E
B
2
1
∵AB ⊥ BD, CD ⊥ BD, ∠1= ∠2
∴△ABE∽△CDE
∴
∴
已知观察者的脚与镜子的距离BE、 旗杆底部与镜子的距离DE、观察者的眼睛到地面的高度AB,则可求出旗杆的高度
“利用镜子的反射测量高度”的原理解决.
A
C
E
B
D
测量数据:人眼睛到地面高度AB、人与镜子间的距离BE、旗杆与镜子间距离DE.
找相似:△ABE∽△CDE.
找比例:AB:CD=BE:DE
B
D
C
A
E
典例精析
例1:如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
解析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
例2:为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
解得 BA=18.75(m).
因此,树高约为18.75m.
D
B
A
C
E
2
1
当堂练习
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第四章 图形的相似
4.6 利用相似三角形测高
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、通过测量旗杆高度学会相似三角形的实际应用,复习巩固相似三角形的相关知识点;
2、可以灵活运用相似三角形的性质解决实际问题;
导入新课
温故知新
问题:相似三角形的判定方法有哪些?
① 两角对应相等,两三角形相似.
② 两边对应成比例且夹角相等,两三角形相似.
③ 三边对应成比例,两三角形相似.
B’
A’
C’
B
A
C
观察与思考
胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗?
探究活动:利用相似三角形的有关知识测量旗杆的高度
活动工具:小镜子、标杆、皮尺等测量工具
活动方式:分组活动、全班交流研讨
讲授新课
知识点一 运用相似三角形解决高度(长度)问题
例1:如下图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
解:∵BF∥ED,∴∠BAO=∠EDF,
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴ = ,∴ = ,
∴BO=134.
因此金字塔高134 m.
方法1:利用阳光下的影子
选一名同学直立在旗杆旁边,在同一时刻下测出该同学和旗杆的影子长,并测量出该同学的身高,根据上面的数据,你能求出旗杆的高度吗?
D
F
E
A
B
C
A
B
C
D
E
F
A
D
F
E
B
C
∵AB∥DE
∵B、C、E、F在一条直线上
∴△ABC∽△DEF
∴
∴
同学的身高AC、同学影长BC、同一时刻旗杆的影长EF均可测量得出,所以代入测量数据即可求出旗杆DF的高度
物1高 :物2高 = 影1长 :影2长
测高方法一:利用阳光下的影子
测量不能到达顶部的物体的高度,可以用“在同一时刻物高与影长成正比例”的原理解决.
归纳总结
测量数据:身高AC、影长BC、旗杆影长EF.
方法2:利用标杆
选一名同学作为观察者,观察者与旗杆之间的地面直立一根高度适当的标杆,观测者调整自己的位置,使旗杆顶部、标杆顶部与眼睛恰好在同一直线上
方法2:利用标杆
测出观察者的脚到旗杆的距离,及到标杆的距离,观察者眼睛到地面的高度,标杆的高,你能求出旗杆的高吗?
C
E
B
F
D
3
M
N
1
2
A
需要测量的数据:
人与标杆的距离AM
人与旗杆的距离AN
标杆的高度EF
人眼到地面的距离AB
过A作AN⊥CD交DC于点N,交EF于M
∵EF∥CN
∴△AME∽△ANC
A
B
C
D
E
F
M
N
∴
∴
∵四边形ABDN为矩形
∴DN=AB
∴CD=CN+DN
方法2:利用标杆
C
E
B
F
A
D
构造相似:△AME∽△ANC.
找比例:AM:AN=EM:CN
M
N
需要测量的数据:
人与标杆的距离AM
人与旗杆的距离AN
标杆的高度EF
方法3:利用镜子反射
A
C
D
E
B
平面镜
操作:1.选一名学生作为观测者,在他与旗杆之间的地面上平放一面镜子,固定镜子的位置;
2.观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,
方法3:利用镜子反射
A
C
D
E
B
平面镜
3.测出观察者的脚与镜子的距离BE、
旗杆底部与镜子的距离DE、
观察者的眼睛到地面的高度AB
那么能求出旗杆的高度吗?
A
C
D
E
B
平面镜
方法3:利用镜子反射
A
C
D
E
B
2
1
∵AB ⊥ BD, CD ⊥ BD, ∠1= ∠2
∴△ABE∽△CDE
∴
∴
已知观察者的脚与镜子的距离BE、 旗杆底部与镜子的距离DE、观察者的眼睛到地面的高度AB,则可求出旗杆的高度
“利用镜子的反射测量高度”的原理解决.
A
C
E
B
D
测量数据:人眼睛到地面高度AB、人与镜子间的距离BE、旗杆与镜子间距离DE.
找相似:△ABE∽△CDE.
找比例:AB:CD=BE:DE
B
D
C
A
E
典例精析
例1:如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
解析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交ID于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6(m),
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
例2:为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
解得 BA=18.75(m).
因此,树高约为18.75m.
D
B
A
C
E
2
1
当堂练习
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
