6.1 反比例函数 课件(30张PPT)
文档属性
| 名称 | 6.1 反比例函数 课件(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 17:24:57 | ||
图片预览










文档简介
(共30张PPT)
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第六章 反比例函数
6.1 反比例函数
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握反比例函数的概念,注意反比例函数函数k值的范围;
2、学会区分反比例函数和一次函数的区别,知道反比例函数的特征;
3、根据所给条件求反比例函数解析式;
导入新课
情境引入
?
新学期伊始,小明想买一些笔记本为以后的学习做准备. 妈妈给了小明 30 元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元 1.5 2 2.5 3 5 7.5 …
购买的笔记本数量y/本
通过填表,你发现 x,y 之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
讲授新课
知识点一 反比例函数的概念
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1) 京沪线铁路全程为1463 km,某次列车的平均速
度v (单位:km/h) 随此次列车的全程运行时间 t
(单位:h) 的变化而变化;
(2) 某住宅小区要种植一块面积为 1000 m2 的矩形草
坪,草坪的长 y (单位:m) 随宽 x (单位:m)的
变化而变化;
(3) 已知北京市的总面积为1.68×104 km2 ,人均占
有面积 S (km2/人) 随全市总人口 n (单位:人) 的
变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有 的形式,其中 是常数.
分式
分子
(k为常数,k ≠ 0) 的函数,
叫做反比例函数,其中 x 是自变量,y 是函数.
一般地,形如
反比例函数 (k≠0) 的自变量 x 的取值范围是什么?
思考:
因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数.
但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
例如,在前面得到的第一个解析式
中,t 的取值范围是 t>0,且当 t 取每一个确定的
值时,v 都有唯一确定的值与其对应.
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
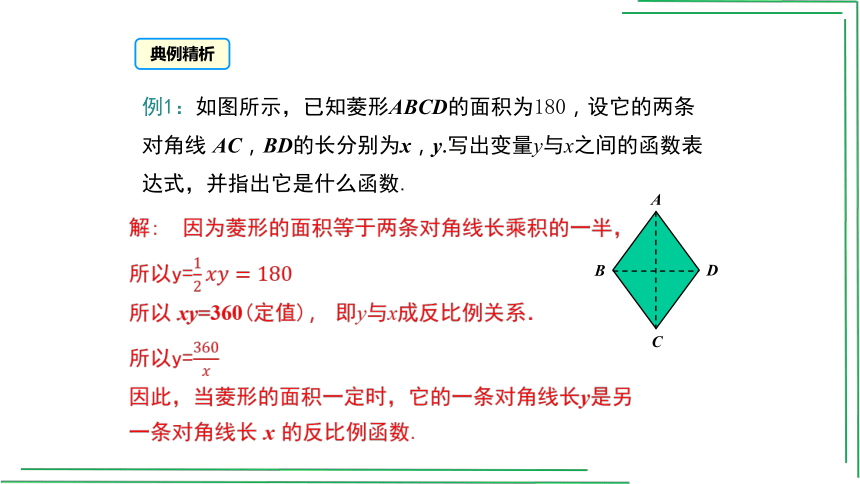
解: 因为菱形的面积等于两条对角线长乘积的一半,
所以y=
所以 xy=360(定值), 即y与x成反比例关系.
所以y=
因此,当菱形的面积一定时,它的一条对角线长y是另一条对角线长 x 的反比例函数.
例1:如图所示,已知菱形ABCD的面积为180,设它的两条对角线 AC,BD的长分别为x,y.写出变量y与x之间的函数表达式,并指出它是什么函数.
A
B
C
D
典例精析
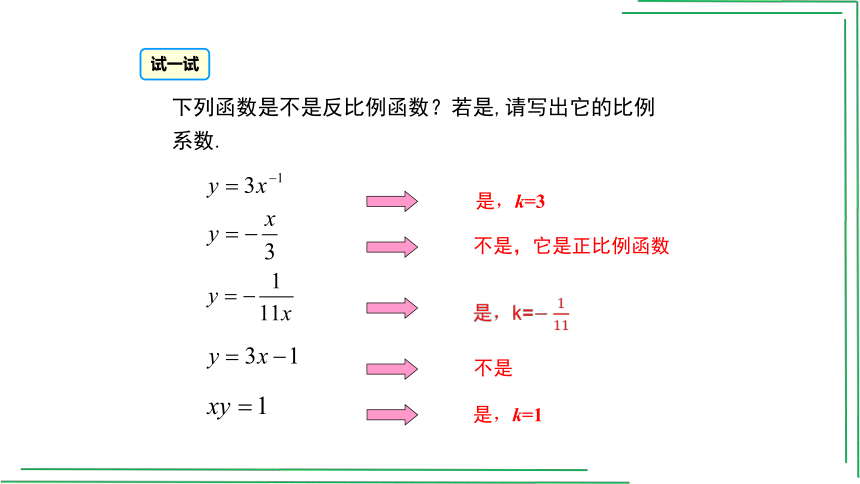
试一试
下列函数是不是反比例函数?若是,请写出它的比例系数.
是,k=3
不是,它是正比例函数
不是
是,k=1
是,k=
知识点二 用待定系数法求反比例函数解析式
典例精析
例2:已知y是x的反比例函数,当x=-4时,y=3.
(1)写出y与x之间的函数表达式;
(2)当x=-2时,求y的值;
(3)当y=12时,求x的值.
解:(1)设
∵当x=-4时,y=3,
∴3= ,解得k=-12.
因此,y和x之间的函数表达式为y=- ;
(2)把x=-2代入y=- ,得y=- =6;
(3)把y=12 代入y=- ,得12=- ,x=-1.
(1)求反比例函数表达式时常用待定系数法,先设其表达式为y=kx(k≠0),然后再求出k值;
(2)当反比例函数的表达式y=kx(k≠0)确定以后,已知x(或y)的值,将其代入表达式中即可求得相应的y(或x)的值.
总结
例3:已知y与x-1成反比例,当x = 2时,y = 4.
(1)用含有x的代数式表示y;
(2)当x=3时,求y的值.
解:(1)设y = (k≠0),
因为当 x=2时,y=4,所以4= ,
解得 k = 4.
所以y 与 x 的函数表达式是y= ;
(2)当x = 3时,y= =2.
当堂练习
课堂小结
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第六章 反比例函数
6.1 反比例函数
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、掌握反比例函数的概念,注意反比例函数函数k值的范围;
2、学会区分反比例函数和一次函数的区别,知道反比例函数的特征;
3、根据所给条件求反比例函数解析式;
导入新课
情境引入
?
新学期伊始,小明想买一些笔记本为以后的学习做准备. 妈妈给了小明 30 元钱,小明可以如何选择笔记本的价钱和数量呢?
笔记本单价x/元 1.5 2 2.5 3 5 7.5 …
购买的笔记本数量y/本
通过填表,你发现 x,y 之间具有怎样的关系?你还能举出这样的例子吗?
20
15
12
10
6
4
?
讲授新课
知识点一 反比例函数的概念
下列问题中,变量间具有函数关系吗?如果有,请写出它们的解析式.
合作探究
(1) 京沪线铁路全程为1463 km,某次列车的平均速
度v (单位:km/h) 随此次列车的全程运行时间 t
(单位:h) 的变化而变化;
(2) 某住宅小区要种植一块面积为 1000 m2 的矩形草
坪,草坪的长 y (单位:m) 随宽 x (单位:m)的
变化而变化;
(3) 已知北京市的总面积为1.68×104 km2 ,人均占
有面积 S (km2/人) 随全市总人口 n (单位:人) 的
变化而变化.
观察以上三个解析式,你觉得它们有什么共同特点?
问题:
都具有 的形式,其中 是常数.
分式
分子
(k为常数,k ≠ 0) 的函数,
叫做反比例函数,其中 x 是自变量,y 是函数.
一般地,形如
反比例函数 (k≠0) 的自变量 x 的取值范围是什么?
思考:
因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数.
但实际问题中,应根据具体情况来确定反比例函数自变量的取值范围.
例如,在前面得到的第一个解析式
中,t 的取值范围是 t>0,且当 t 取每一个确定的
值时,v 都有唯一确定的值与其对应.
反比例函数除了可以用 (k ≠ 0) 的形式表示,还有没有其他表达方式?
想一想:
反比例函数的三种表达方式:(注意 k ≠ 0)
解: 因为菱形的面积等于两条对角线长乘积的一半,
所以y=
所以 xy=360(定值), 即y与x成反比例关系.
所以y=
因此,当菱形的面积一定时,它的一条对角线长y是另一条对角线长 x 的反比例函数.
例1:如图所示,已知菱形ABCD的面积为180,设它的两条对角线 AC,BD的长分别为x,y.写出变量y与x之间的函数表达式,并指出它是什么函数.
A
B
C
D
典例精析
试一试
下列函数是不是反比例函数?若是,请写出它的比例系数.
是,k=3
不是,它是正比例函数
不是
是,k=1
是,k=
知识点二 用待定系数法求反比例函数解析式
典例精析
例2:已知y是x的反比例函数,当x=-4时,y=3.
(1)写出y与x之间的函数表达式;
(2)当x=-2时,求y的值;
(3)当y=12时,求x的值.
解:(1)设
∵当x=-4时,y=3,
∴3= ,解得k=-12.
因此,y和x之间的函数表达式为y=- ;
(2)把x=-2代入y=- ,得y=- =6;
(3)把y=12 代入y=- ,得12=- ,x=-1.
(1)求反比例函数表达式时常用待定系数法,先设其表达式为y=kx(k≠0),然后再求出k值;
(2)当反比例函数的表达式y=kx(k≠0)确定以后,已知x(或y)的值,将其代入表达式中即可求得相应的y(或x)的值.
总结
例3:已知y与x-1成反比例,当x = 2时,y = 4.
(1)用含有x的代数式表示y;
(2)当x=3时,求y的值.
解:(1)设y = (k≠0),
因为当 x=2时,y=4,所以4= ,
解得 k = 4.
所以y 与 x 的函数表达式是y= ;
(2)当x = 3时,y= =2.
当堂练习
课堂小结
建立反比例函数模型
用待定系数法求反比例函数解析式
反比例函数:定义/三种表达方式
反比例函数
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
