6.2 反比例函数的图象和性质(第2课时) 课件(30张PPT)
文档属性
| 名称 | 6.2 反比例函数的图象和性质(第2课时) 课件(30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 08:44:20 | ||
图片预览






文档简介
(共30张PPT)
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第六章 反比例函数
6.2 反比例函数的图象和性质
第2课时 反比例函数的性质
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握反比例函数的性质,并灵活运用;
2、理解反比例函数k值的意义,掌握反比例函数的单调性;
3、运用反比例函数的性质解决实际问题;
导入新课
情境引入
问题:下表是一个反比例函数的部分取值,想一想这些点如果在直角坐标系中是怎样一种情况呢?可以试着动手画一画.
x -6 -3 -2 -1 1 2 3 6
y -1 -2 -3 -6 6 3 2 1
x -6 -3 -2 -1 1 2 3 6
y 1 2 6 6 -6 -3 -2 -1
讲授新课
知识点一 反比例函数的性质
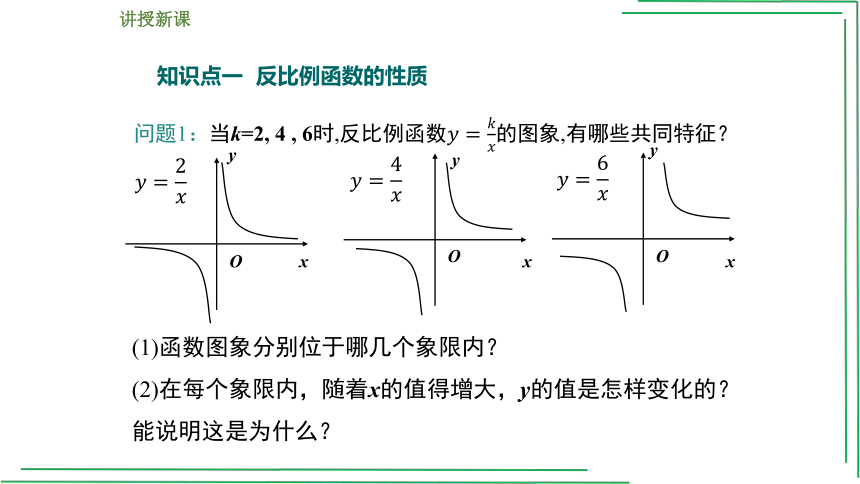
问题1:当k=2, 4 , 6时,反比例函数的图象,有哪些共同特征?
(1)函数图象分别位于哪几个象限内?
(2)在每个象限内,随着x的值得增大,y的值是怎样变化的?能说明这是为什么?
y
y
y
x
x
x
O
O
O
概念归纳
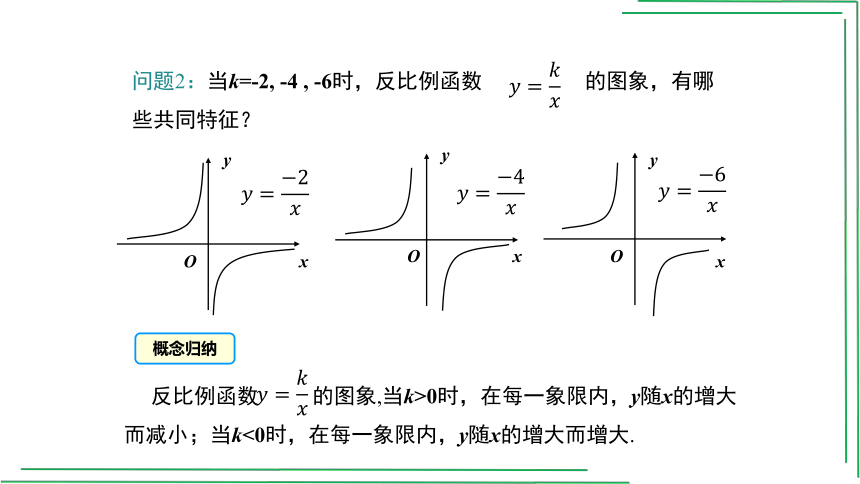
问题2:当k=-2, -4 , -6时,反比例函数 的图象,有哪些共同特征?
反比例函数 的图象,当k>0时,在每一象限内,y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大.
y
y
y
x
x
x
O
O
O
知识点二 反比例函数解析式中 k 的几何意义
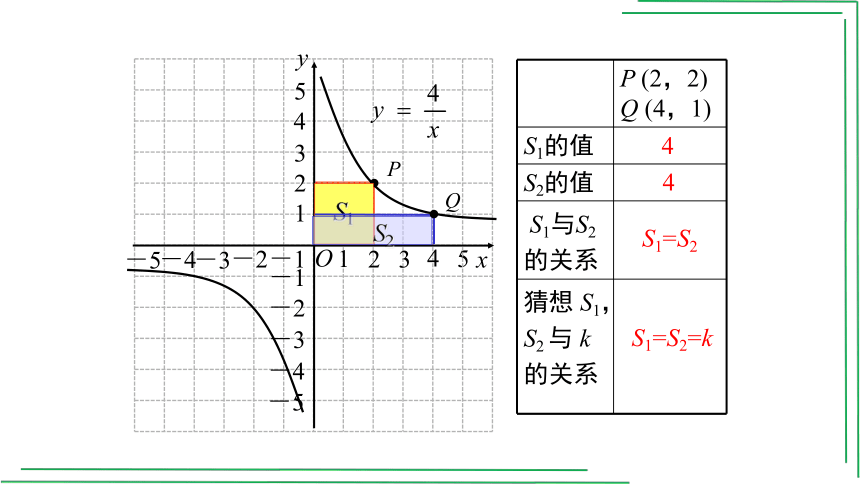
1. 在反比例函数 的图象上分别取点P,Q 向
x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,
填写下页表格:
合作探究
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
猜想 S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
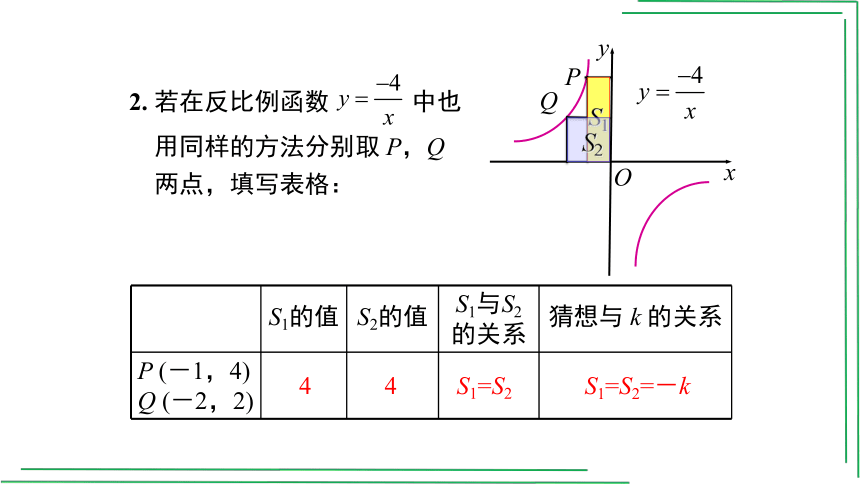
S1的值 S2的值 S1与S2的关系 猜想与 k 的关系
P (-1,4) Q (-2,2)
2. 若在反比例函数 中也
用同样的方法分别取 P,Q
两点,填写表格:
4
4
S1=S2
S1=S2=-k
y
x
O
P
Q
S1
S2
由前面的探究过程,可以猜想:
若点P是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,矩形 AOBP 的面积与k
的关系是S矩形 AOBP=|k|.
y
x
O
P
S
我们就 k < 0 的情况给出证明:
设点 P 的坐标为 (a,b)
A
B
∵点 P (a,b) 在函数 的图
象上,
∴ ,即 ab=k.
∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;
若点 P 在第二象限,则 a<0,b>0,
若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP=PB·PA
=a· (-b)=-ab=-k.
B
P
A
综上,S矩形 AOBP=|k|.
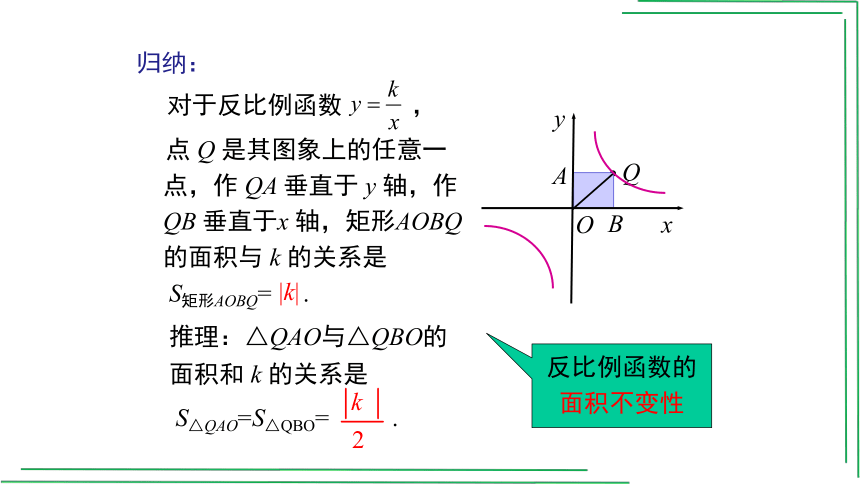
点 Q 是其图象上的任意一
点,作 QA 垂直于 y 轴,作
QB 垂直于x 轴,矩形AOBQ
的面积与 k 的关系是
S矩形AOBQ= .
推理:△QAO与△QBO的
面积和 k 的关系是
S△QAO=S△QBO= .
Q
对于反比例函数 ,
A
B
|k|
y
x
O
归纳:
反比例函数的面积不变性
如图所示,直线与双曲线交于 A,B 两点,P 是AB 上的点,△ AOC 的面积 S1、△ BOD 的面积 S2、 △ POE 的面积 S3 的大小关系为 .
S1 = S2 < S3
练一练
解析:由反比例函数面积的不变
性易知 S1 = S2. PE 与双曲线的一
支交于点 F,连接 OF,易知,
S△OFE = S1 = S2,而 S3>S△OFE,
所以 S1,S2,S3的大小关系为
S1 = S2 < S3
F
S1
S2
S3
当堂练习
课堂小结
反比例函数 (k≠0) k k > 0 k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第六章 反比例函数
6.2 反比例函数的图象和性质
第2课时 反比例函数的性质
精品教学课件
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、熟练掌握反比例函数的性质,并灵活运用;
2、理解反比例函数k值的意义,掌握反比例函数的单调性;
3、运用反比例函数的性质解决实际问题;
导入新课
情境引入
问题:下表是一个反比例函数的部分取值,想一想这些点如果在直角坐标系中是怎样一种情况呢?可以试着动手画一画.
x -6 -3 -2 -1 1 2 3 6
y -1 -2 -3 -6 6 3 2 1
x -6 -3 -2 -1 1 2 3 6
y 1 2 6 6 -6 -3 -2 -1
讲授新课
知识点一 反比例函数的性质
问题1:当k=2, 4 , 6时,反比例函数的图象,有哪些共同特征?
(1)函数图象分别位于哪几个象限内?
(2)在每个象限内,随着x的值得增大,y的值是怎样变化的?能说明这是为什么?
y
y
y
x
x
x
O
O
O
概念归纳
问题2:当k=-2, -4 , -6时,反比例函数 的图象,有哪些共同特征?
反比例函数 的图象,当k>0时,在每一象限内,y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大.
y
y
y
x
x
x
O
O
O
知识点二 反比例函数解析式中 k 的几何意义
1. 在反比例函数 的图象上分别取点P,Q 向
x 轴、y 轴作垂线,围成面积分别为S1,S2的矩形,
填写下页表格:
合作探究
5
1
2
3
4
-1
5
x
y
O
P
S1
S2
P (2,2)
Q (4,1)
S1的值
S2的值
S1与S2的关系
猜想 S1,S2 与 k的关系
4
4
S1=S2
S1=S2=k
-5
-4
-3
-2
1
4
3
2
-3
-2
-4
-5
-1
Q
S1的值 S2的值 S1与S2的关系 猜想与 k 的关系
P (-1,4) Q (-2,2)
2. 若在反比例函数 中也
用同样的方法分别取 P,Q
两点,填写表格:
4
4
S1=S2
S1=S2=-k
y
x
O
P
Q
S1
S2
由前面的探究过程,可以猜想:
若点P是 图象上的任意一点,作 PA 垂直于 x 轴,作 PB 垂直于 y 轴,矩形 AOBP 的面积与k
的关系是S矩形 AOBP=|k|.
y
x
O
P
S
我们就 k < 0 的情况给出证明:
设点 P 的坐标为 (a,b)
A
B
∵点 P (a,b) 在函数 的图
象上,
∴ ,即 ab=k.
∴ S矩形 AOBP=PB·PA=-a·b=-ab=-k;
若点 P 在第二象限,则 a<0,b>0,
若点 P 在第四象限,则 a>0,b<0,
∴ S矩形 AOBP=PB·PA
=a· (-b)=-ab=-k.
B
P
A
综上,S矩形 AOBP=|k|.
点 Q 是其图象上的任意一
点,作 QA 垂直于 y 轴,作
QB 垂直于x 轴,矩形AOBQ
的面积与 k 的关系是
S矩形AOBQ= .
推理:△QAO与△QBO的
面积和 k 的关系是
S△QAO=S△QBO= .
Q
对于反比例函数 ,
A
B
|k|
y
x
O
归纳:
反比例函数的面积不变性
如图所示,直线与双曲线交于 A,B 两点,P 是AB 上的点,△ AOC 的面积 S1、△ BOD 的面积 S2、 △ POE 的面积 S3 的大小关系为 .
S1 = S2 < S3
练一练
解析:由反比例函数面积的不变
性易知 S1 = S2. PE 与双曲线的一
支交于点 F,连接 OF,易知,
S△OFE = S1 = S2,而 S3>S△OFE,
所以 S1,S2,S3的大小关系为
S1 = S2 < S3
F
S1
S2
S3
当堂练习
课堂小结
反比例函数 (k≠0) k k > 0 k < 0
图象
性质
图象位于第一、三象限
图象位于第二、四象限
在每个象限内,y 随 x 的增大而减小
在每个象限内,y 随
x 的增大而增大
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
