专题09 立体几何与空间向量讲义 -2023届新高考1卷高考二轮复习 解答题篇(无答案)
文档属性
| 名称 | 专题09 立体几何与空间向量讲义 -2023届新高考1卷高考二轮复习 解答题篇(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 21:26:40 | ||
图片预览


文档简介
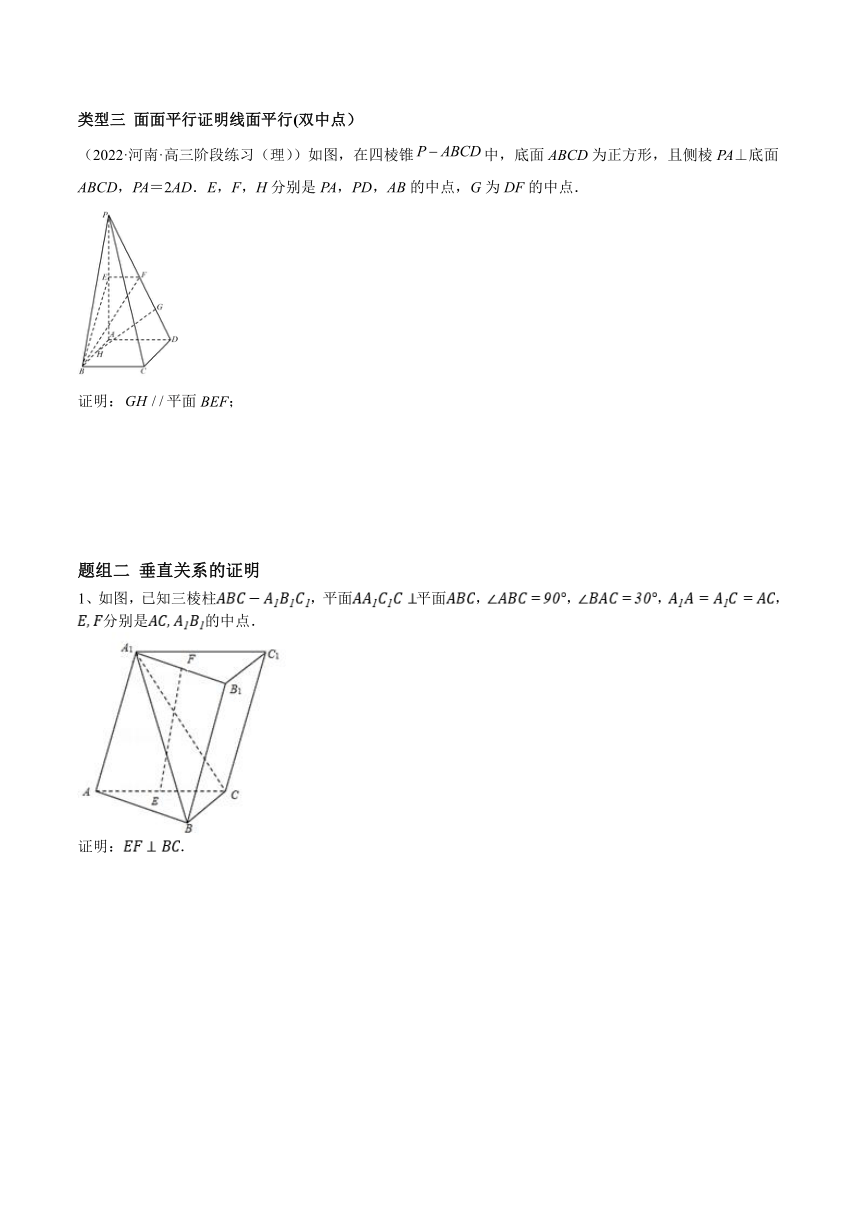
专题09 运用空间向量研究立体几何问题
平行
垂直
角 异面直线角:平移 线面角:作平面垂线(由面面垂直得线面垂直) 二面角:作三垂线(由等体积法求垂线长)
题组一 平行关系的证明
类型一 线线平行证明线面平行
中位线法
1.已知四棱锥中,底面为矩形,平面平面,,点E,F分别是,的中点.
求证: 平面.
平行四边形法
2.在四棱锥P-ABCD中,,,,点E在棱PD上,且.
求证:AE∥平面PBC;
类型二 线面平行证明线线平行
(2021·长沙市·湖南师大附中高三二模)如图,在四棱锥中,,,,△是边长为2的等边三角形,平面平面,为线段上一点.
设平面平面,证明:平面;
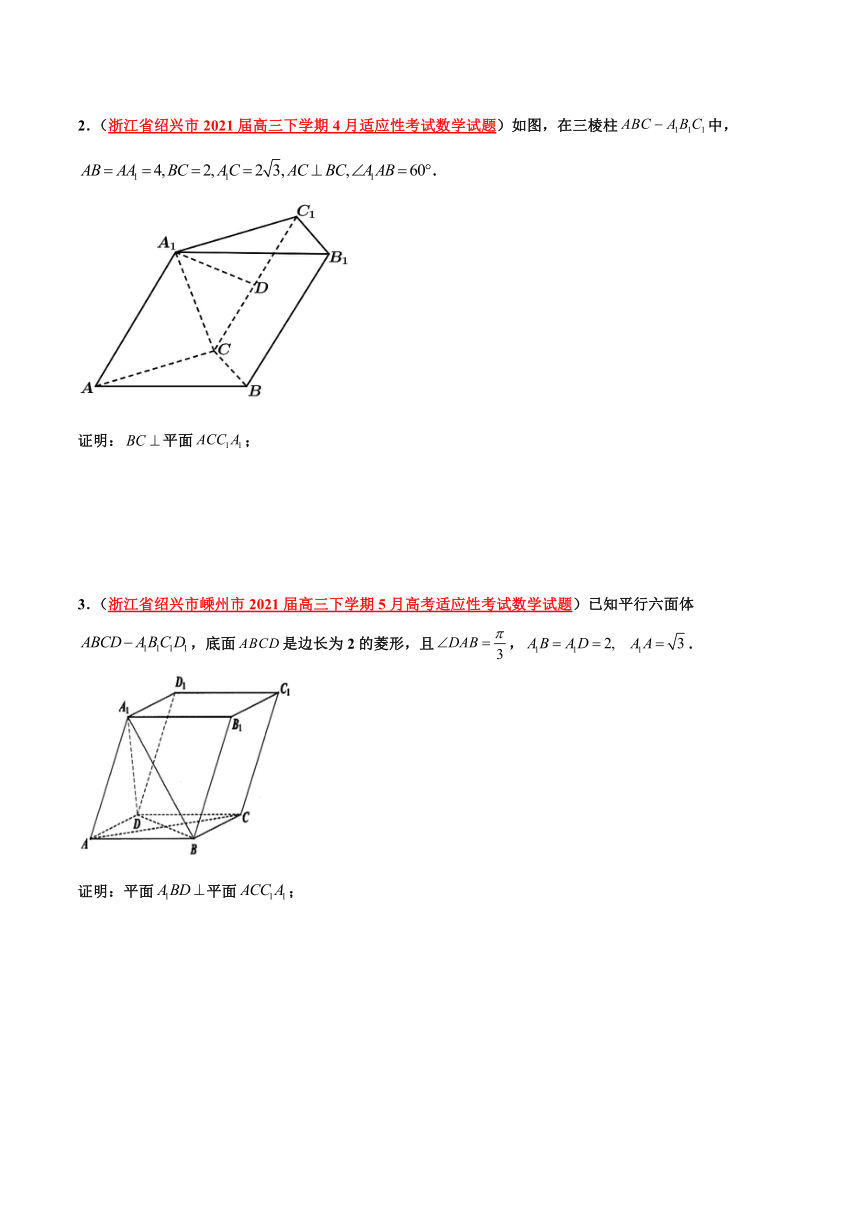
类型三 面面平行证明线面平行(双中点)
(2022·河南·高三阶段练习(理))如图,在四棱锥中,底面ABCD为正方形,且侧棱PA⊥底面ABCD,PA=2AD.E,F,H分别是PA,PD,AB的中点,G为DF的中点.
证明:平面BEF;
题组二 垂直关系的证明
1、如图,已知三棱柱,平面平面,,,,分别是的中点.
证明:.
2.(浙江省绍兴市2021届高三下学期4月适应性考试数学试题)如图,在三棱柱中,.
证明:平面;
3.(浙江省绍兴市嵊州市2021届高三下学期5月高考适应性考试数学试题)已知平行六面体,底面是边长为2的菱形,且,.
证明:平面平面;
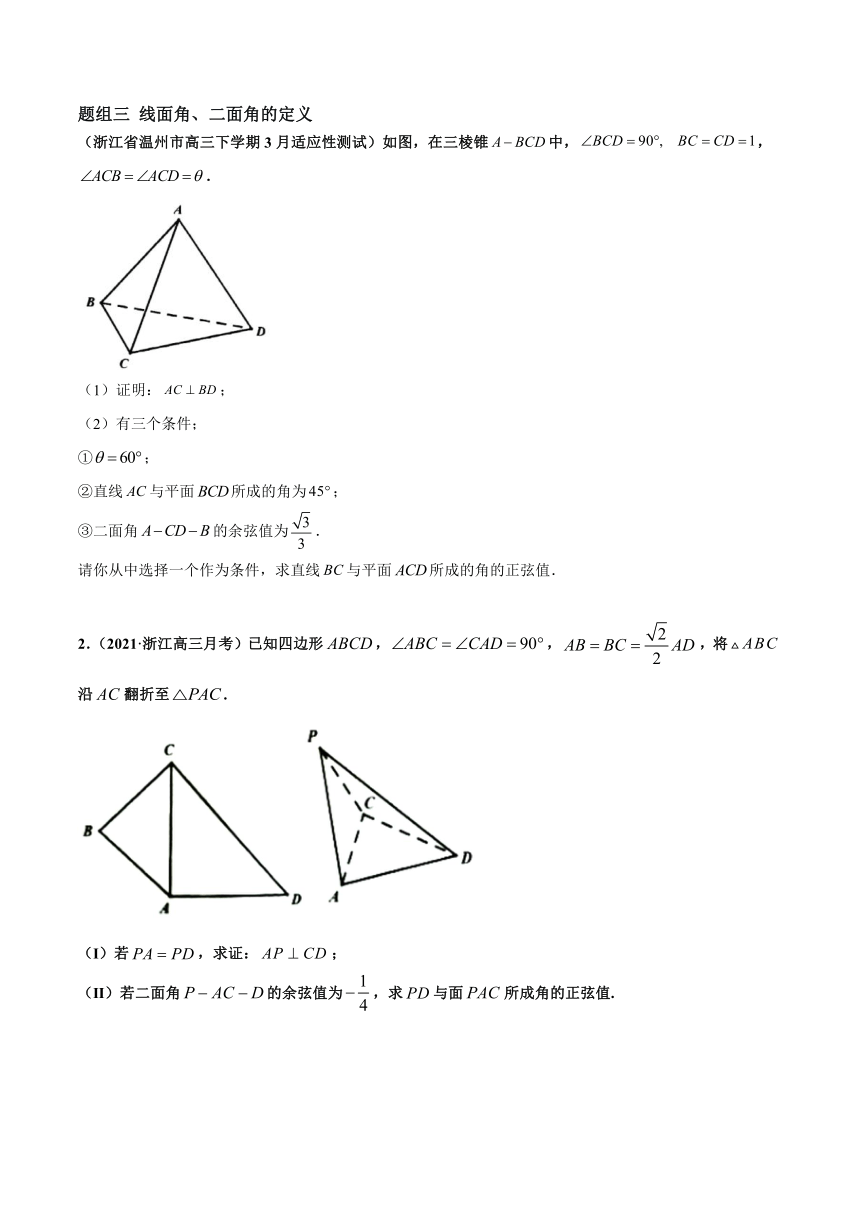
题组三 线面角、二面角的定义
(浙江省温州市高三下学期3月适应性测试)如图,在三棱锥中,,.
(1)证明:;
(2)有三个条件;
①;
②直线与平面所成的角为;
③二面角的余弦值为.
请你从中选择一个作为条件,求直线与平面所成的角的正弦值.
2.(2021·浙江高三月考)已知四边形,,,将沿翻折至.
(Ⅰ)若,求证:;
(Ⅱ)若二面角的余弦值为,求与面所成角的正弦值.
题组四 点到平面的距离
如图,在三棱锥中,是边长为4的正三角形, ,分别为的中点,且.求点到平面的距离.
题组五 线面角、二面角的几何求法
类型一 线面角几何求法——等体积法
(浙江省绍兴市上虞区2021届高三下学期第二次教学质量检测数学试题)已知三棱锥,是等腰直角三角形,是等边三角形,且,,.
(Ⅰ)求证:;
(Ⅱ)求直线与平面所成角的正弦值
类型二 二面角几何求法——垂面法
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体.
(1)求证BC⊥平面AFG.
(2)求二面角B-AE-D的余弦值.
类型三 二面角几何求法——三垂线定理
如图, 和 所在平面互相垂直,且 ,,, 分
别为 , 的中点.
(1) 求证:;
(2) 求二面角 的正弦值
题组六、探索性问题
1、(2021·山东滨州市·高三二模)如图,在四棱锥中,O是BD的中点,平面ABCD,,,.
(1)求证:平面平面;
(2)设,若二面角的余弦值为,求的值.
2、(2021·福建厦门双十中学高三其他模拟)已知四棱锥E—ABCD中,四边形ABCD为等腰梯形,AB∥DC,AD=DC=2,AB=4,△ADE为等边三角形,且平面ADE⊥平面ABCD.
(1)求证:AE⊥BD;
(2)是否存在一点F,满足 (0<≤1),且使平面ADF与平面BCE所成的锐二面角的余弦值为.若存在,求出的值,否则请说明理由.
题组七、线面角、二面角的空间向量求法
类型一 线面角
1、(2021·山东聊城市·高三三模)如图,在平面四边形ABCD中,,,,以BD为折痕把折起,使点A到达点P的位置,且.
(1)证明:;
(2)若M为PB的中点,二面角的大小为60°,求直线PC与平面MCD所成角的正弦值.
2、(2021·山东泰安市·高三其他模拟)如图,圆柱的高为3,是圆柱的下底面圆的内接三角形,是上底面圆内的一条弦,均为圆柱的母线,且分别为的中点.
(1)求证:平面;
(2)若是等边三角形,求直线与平面所成角的正弦值.
类型二、面面角
1、(2021·河北邯郸市高三三模)在三棱柱中,底面,为正三角形,,是的中点.
(1)求证:平面平面;
(2)求二面角的余弦值.
2、(2021·山东泰安市·高三三模)已知三棱柱,,,,点为中点.
(1)试确定线段上一点,使平面;
(2)在(1)的条件下,若平面平面, ,求平面 与平面所成锐二面角的余弦值.
1、(2021·山东青岛市·高三二模)如图,在直三棱柱中,底面三角形为直角三角形,其中,,,,,分别为和的中点.
(1)求证:平面;
(2)当点在线段上移动时,求直线与平面所成角正弦的最大值.
2、(2021·长沙市·湖南师大附中高三二模)如图,在四棱锥中,,,,△是边长为2的等边三角形,平面平面,为线段上一点.
(1)设平面平面,证明:平面;
(2)是否存在这样点,使平面与平面所成角为,如果存在,求的值;如果不存在,请说明理由.
3.(浙江省丽水、湖州、衢州三地市2021届高三下学期4月教学质量检测数学试题)已知三棱柱,是正三角形,四边形是菱形且,是的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
4.如图,在四棱锥中,分别是的中点,底面是边长为2的正方形,,且平面平面.
(1)求证:平面平面;
(2)求二面角所成角的余弦值.
1、(2021年全国高考乙卷数学(理)试题)如图,四棱锥的底面是矩形,底面,,为的中点,且.
(1)求;
(2)求二面角的正弦值.
2、(2021年全国高考甲卷数学(理)试题)已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
3、(2020全国Ⅰ理18)如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
4、(2020天津17)如图,在三棱柱中,平面,,点分别在棱和棱上,且为棱的中点.
(Ⅰ)求证:;
(Ⅱ)求二面角的正弦值;
(Ⅲ)求直线与平面所成角的正弦值.
5、(2020山东20)如图,四棱锥的底面为正方形,底面,设平面与平面的交线为.
(1)证明:平面;
(2)已知,为上的点,求与平面所成角的正弦值的最大值.
6、(2019 新课标Ⅰ,理18)如图,直四棱柱的底面是菱形,,,,,,分别是,,的中点.
(1)证明:平面;
(2)求二面角的正弦值.
7. (2022 全国甲卷理科)在四棱锥中,底面.
(1)证明:;
(2)求PD与平面所成的角的正弦值.
8、(2022 全国新高考1卷).如图,直三棱柱 的体积为4, '的面积为
(1)求A到平面 的距离;
(2)设D为 的中点, 平面 平面 求二面角 的正弦值.
9.(2022 全国乙卷理科)如图,四面体中,,E为的中点.
(1)证明:平面平面;
(2)设,点F在上,当的面积最小时,求与平面所成的角的正弦值.
10. (2022 全国新高考2卷)如图,是三棱锥高,,,E是的中点.
(1)证明:平面;
(2)若,,,求二面角的正弦值.
平行
垂直
角 异面直线角:平移 线面角:作平面垂线(由面面垂直得线面垂直) 二面角:作三垂线(由等体积法求垂线长)
题组一 平行关系的证明
类型一 线线平行证明线面平行
中位线法
1.已知四棱锥中,底面为矩形,平面平面,,点E,F分别是,的中点.
求证: 平面.
平行四边形法
2.在四棱锥P-ABCD中,,,,点E在棱PD上,且.
求证:AE∥平面PBC;
类型二 线面平行证明线线平行
(2021·长沙市·湖南师大附中高三二模)如图,在四棱锥中,,,,△是边长为2的等边三角形,平面平面,为线段上一点.
设平面平面,证明:平面;
类型三 面面平行证明线面平行(双中点)
(2022·河南·高三阶段练习(理))如图,在四棱锥中,底面ABCD为正方形,且侧棱PA⊥底面ABCD,PA=2AD.E,F,H分别是PA,PD,AB的中点,G为DF的中点.
证明:平面BEF;
题组二 垂直关系的证明
1、如图,已知三棱柱,平面平面,,,,分别是的中点.
证明:.
2.(浙江省绍兴市2021届高三下学期4月适应性考试数学试题)如图,在三棱柱中,.
证明:平面;
3.(浙江省绍兴市嵊州市2021届高三下学期5月高考适应性考试数学试题)已知平行六面体,底面是边长为2的菱形,且,.
证明:平面平面;
题组三 线面角、二面角的定义
(浙江省温州市高三下学期3月适应性测试)如图,在三棱锥中,,.
(1)证明:;
(2)有三个条件;
①;
②直线与平面所成的角为;
③二面角的余弦值为.
请你从中选择一个作为条件,求直线与平面所成的角的正弦值.
2.(2021·浙江高三月考)已知四边形,,,将沿翻折至.
(Ⅰ)若,求证:;
(Ⅱ)若二面角的余弦值为,求与面所成角的正弦值.
题组四 点到平面的距离
如图,在三棱锥中,是边长为4的正三角形, ,分别为的中点,且.求点到平面的距离.
题组五 线面角、二面角的几何求法
类型一 线面角几何求法——等体积法
(浙江省绍兴市上虞区2021届高三下学期第二次教学质量检测数学试题)已知三棱锥,是等腰直角三角形,是等边三角形,且,,.
(Ⅰ)求证:;
(Ⅱ)求直线与平面所成角的正弦值
类型二 二面角几何求法——垂面法
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体.
(1)求证BC⊥平面AFG.
(2)求二面角B-AE-D的余弦值.
类型三 二面角几何求法——三垂线定理
如图, 和 所在平面互相垂直,且 ,,, 分
别为 , 的中点.
(1) 求证:;
(2) 求二面角 的正弦值
题组六、探索性问题
1、(2021·山东滨州市·高三二模)如图,在四棱锥中,O是BD的中点,平面ABCD,,,.
(1)求证:平面平面;
(2)设,若二面角的余弦值为,求的值.
2、(2021·福建厦门双十中学高三其他模拟)已知四棱锥E—ABCD中,四边形ABCD为等腰梯形,AB∥DC,AD=DC=2,AB=4,△ADE为等边三角形,且平面ADE⊥平面ABCD.
(1)求证:AE⊥BD;
(2)是否存在一点F,满足 (0<≤1),且使平面ADF与平面BCE所成的锐二面角的余弦值为.若存在,求出的值,否则请说明理由.
题组七、线面角、二面角的空间向量求法
类型一 线面角
1、(2021·山东聊城市·高三三模)如图,在平面四边形ABCD中,,,,以BD为折痕把折起,使点A到达点P的位置,且.
(1)证明:;
(2)若M为PB的中点,二面角的大小为60°,求直线PC与平面MCD所成角的正弦值.
2、(2021·山东泰安市·高三其他模拟)如图,圆柱的高为3,是圆柱的下底面圆的内接三角形,是上底面圆内的一条弦,均为圆柱的母线,且分别为的中点.
(1)求证:平面;
(2)若是等边三角形,求直线与平面所成角的正弦值.
类型二、面面角
1、(2021·河北邯郸市高三三模)在三棱柱中,底面,为正三角形,,是的中点.
(1)求证:平面平面;
(2)求二面角的余弦值.
2、(2021·山东泰安市·高三三模)已知三棱柱,,,,点为中点.
(1)试确定线段上一点,使平面;
(2)在(1)的条件下,若平面平面, ,求平面 与平面所成锐二面角的余弦值.
1、(2021·山东青岛市·高三二模)如图,在直三棱柱中,底面三角形为直角三角形,其中,,,,,分别为和的中点.
(1)求证:平面;
(2)当点在线段上移动时,求直线与平面所成角正弦的最大值.
2、(2021·长沙市·湖南师大附中高三二模)如图,在四棱锥中,,,,△是边长为2的等边三角形,平面平面,为线段上一点.
(1)设平面平面,证明:平面;
(2)是否存在这样点,使平面与平面所成角为,如果存在,求的值;如果不存在,请说明理由.
3.(浙江省丽水、湖州、衢州三地市2021届高三下学期4月教学质量检测数学试题)已知三棱柱,是正三角形,四边形是菱形且,是的中点,.
(1)证明:;
(2)求直线与平面所成角的正弦值.
4.如图,在四棱锥中,分别是的中点,底面是边长为2的正方形,,且平面平面.
(1)求证:平面平面;
(2)求二面角所成角的余弦值.
1、(2021年全国高考乙卷数学(理)试题)如图,四棱锥的底面是矩形,底面,,为的中点,且.
(1)求;
(2)求二面角的正弦值.
2、(2021年全国高考甲卷数学(理)试题)已知直三棱柱中,侧面为正方形,,E,F分别为和的中点,D为棱上的点.
(1)证明:;
(2)当为何值时,面与面所成的二面角的正弦值最小
3、(2020全国Ⅰ理18)如图,为圆锥的顶点,是圆锥底面的圆心,为底面直径,.是底面的内接正三角形,为上一点,.
(1)证明:平面;
(2)求二面角的余弦值.
4、(2020天津17)如图,在三棱柱中,平面,,点分别在棱和棱上,且为棱的中点.
(Ⅰ)求证:;
(Ⅱ)求二面角的正弦值;
(Ⅲ)求直线与平面所成角的正弦值.
5、(2020山东20)如图,四棱锥的底面为正方形,底面,设平面与平面的交线为.
(1)证明:平面;
(2)已知,为上的点,求与平面所成角的正弦值的最大值.
6、(2019 新课标Ⅰ,理18)如图,直四棱柱的底面是菱形,,,,,,分别是,,的中点.
(1)证明:平面;
(2)求二面角的正弦值.
7. (2022 全国甲卷理科)在四棱锥中,底面.
(1)证明:;
(2)求PD与平面所成的角的正弦值.
8、(2022 全国新高考1卷).如图,直三棱柱 的体积为4, '的面积为
(1)求A到平面 的距离;
(2)设D为 的中点, 平面 平面 求二面角 的正弦值.
9.(2022 全国乙卷理科)如图,四面体中,,E为的中点.
(1)证明:平面平面;
(2)设,点F在上,当的面积最小时,求与平面所成的角的正弦值.
10. (2022 全国新高考2卷)如图,是三棱锥高,,,E是的中点.
(1)证明:平面;
(2)若,,,求二面角的正弦值.
同课章节目录
