高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式的关系》能力探究课件(共21张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式的关系》能力探究课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 20:09:24 | ||
图片预览








文档简介
(共21张PPT)
二次函数与一元二次方程、不等式的关系
人教A版同步教材名师课件
---能力探究
解一元二次不等式的方法
分析计算能力
方法1:若不等式对应的一元二次方程能够因式分解,即能够转化为几个代数式的乘积形式,则可以直接由一元二次方程的根及不等号方向得到不等式的解集.
方法2:若不等式对应的一元二次方程能够化为完全平方式,不论取何值,完全平方式始终大于或等于零,易得不等式的解集.
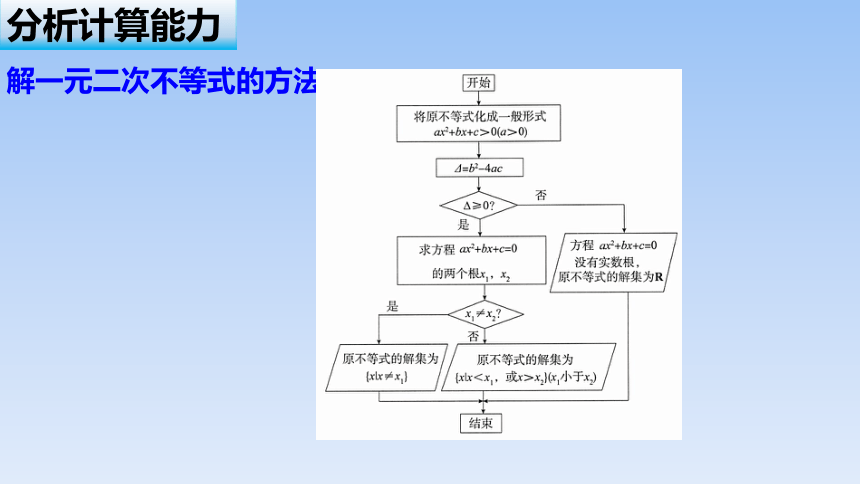
方法3:若上述两种方法均不能解决,则应采用求一元二次不等式的解集的通法,即判别式法,并可用程序框图表示其求解过程.
解一元二次不等式的方法
分析计算能力
典型例题
典例1. (1)不等式的解集为( )
A. B.,或 C. D.
数学运算
解析
(1)不等式变形为,即,得.
D
典型例题
典例1(2)不等式的解集是( )
A. B. C. D.
数学运算
解析
(1)不等式变形为,即,得.
D
典型例题
典例1(3)函数的定义域为( )
A. B. C. D.
数学运算
解析
(3)解不等式组得或.
C
典型例题
典例1(4)若,则不等式的解集为______________.
数学运算
解析
(4)方程的两根为.
又,∴不等式的解集为.
一元二次不等式在R上恒成立问题的方法
简单问题解决能力
已知某个一元二次不等式恒成立,求式子中某些参数的范围是常考的题型之一,主要有以下方法:
(1)利用一元二次方程根的判别式解一元二次不等式在上的恒成立问题.
当未说明不等式为一元二次不等式时,有:
不等式对任意实数恒成立或
一元二次不等式在R上恒成立问题的方法
简单问题解决能力
②不等式对任意实数恒成立
(2)分离自变量和参变量,利用等价转化思想将其转化为求函数的最值问题.
通过等价变换,将参变量从整体中分离出来,转化为
①若在定义城内存在最大值,则(或恒成立(或).
若在定义域内存在最小值,则(或恒成立(或.
典型例题
典例2、(2)已知关于的不等式对一切实数恒成立,则实数的取值范围为______________.
解析
(2)讨论不等式二次项系数,结合判别式即可解答.具体解题过程如下:
①当,即或时,
显然符合条件,不符合条件.
②当时,由二次函数对一切实数恒为正数,得
解得.
结合①②得实数的取值范围是.
数学运算
一元二次不等式在给定区间上恒成立问题
综合问题解决能力
1.两根与的大小比较
一元二次不等式在给定区间上恒成立问题
综合问题解决能力
2.根在区间上的分布
典型例题
典例3-1[数学运算](2019-湖北武汉外校月考)关于的一元二次方程在区间上有实数解,求实数的取值范围.
点拨
本题为一元二次不等式的含参问题,求解此题,根据一元二次方程根的分布情况推出大致图象,借助根与系数的关系即可解答.
数学运算
典型例题
典例3-1[数学运算](2019-湖北武汉外校月考)关于的一元二次方程在区间上有实数解,求实数的取值范围.
解析
设,若在区间上有一个实数解,
∵或解得.若在区间上有两个实数解,
综上,可知的取值范围是.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
点拨
本题结合一元二次方程根的分布情况画出图象.利用数形结合思想解答问题.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
解析
(1)方法一:设函数,作其草图,如右图,
若两实根均大于1,
需即解得.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
解析
(2)若两根,则所以.
(3)若一根大于2,另一根小于2,则,即0,解得.
数学运算
三个“二次”之间的关系的应用
分析计算能力
在解决具体的数学问题时,要注意一元二次不等式及相应的函数与方程三者之间的相互联系,并在一定条件下相互转化.
(1)若一元二次不等式的解集为区间的形式,则区间的端点值恰是相应一元二次方程的根,要注意解集与二次项数的联系.
(2)若已知一元二次方程的根,可以写出相应不等式的解集,反之,已知不等式的解集也可以写出相应二次方程的根,进一步可求得方程中的系数或得到系数之间的关系.
三个“二次”之间的关系的应用
分析计算能力
(3)二次函数与一元二次方程、一元二次不等式三者之间有紧密的关联.一元二次不等式的解集就是二次函数的图象中在轴上方的点的横坐标的集合,一元二次方程的根就是相应二次函数的图象与轴交点的横坐标.
典型例题
典例4(2019-陕西西安一中月考)若不等式的解集是,求不等式的解集.
数学运算
点拨
分析题意可发现要求不等式的解集,
先计算与其相应的一元二次方程的根,注意确定根与系数之间的关系.
典型例题
典例4(2019-陕西西安一中月考)若不等式的解集是,求不等式的解集.
数学运算
解析
由的解集为,知.
又,知.又为方程0的两个根,
∴.又,
∴不等式变为,即.
又∵,所求不等式的解集为.
二次函数与一元二次方程、不等式的关系
人教A版同步教材名师课件
---能力探究
解一元二次不等式的方法
分析计算能力
方法1:若不等式对应的一元二次方程能够因式分解,即能够转化为几个代数式的乘积形式,则可以直接由一元二次方程的根及不等号方向得到不等式的解集.
方法2:若不等式对应的一元二次方程能够化为完全平方式,不论取何值,完全平方式始终大于或等于零,易得不等式的解集.
方法3:若上述两种方法均不能解决,则应采用求一元二次不等式的解集的通法,即判别式法,并可用程序框图表示其求解过程.
解一元二次不等式的方法
分析计算能力
典型例题
典例1. (1)不等式的解集为( )
A. B.,或 C. D.
数学运算
解析
(1)不等式变形为,即,得.
D
典型例题
典例1(2)不等式的解集是( )
A. B. C. D.
数学运算
解析
(1)不等式变形为,即,得.
D
典型例题
典例1(3)函数的定义域为( )
A. B. C. D.
数学运算
解析
(3)解不等式组得或.
C
典型例题
典例1(4)若,则不等式的解集为______________.
数学运算
解析
(4)方程的两根为.
又,∴不等式的解集为.
一元二次不等式在R上恒成立问题的方法
简单问题解决能力
已知某个一元二次不等式恒成立,求式子中某些参数的范围是常考的题型之一,主要有以下方法:
(1)利用一元二次方程根的判别式解一元二次不等式在上的恒成立问题.
当未说明不等式为一元二次不等式时,有:
不等式对任意实数恒成立或
一元二次不等式在R上恒成立问题的方法
简单问题解决能力
②不等式对任意实数恒成立
(2)分离自变量和参变量,利用等价转化思想将其转化为求函数的最值问题.
通过等价变换,将参变量从整体中分离出来,转化为
①若在定义城内存在最大值,则(或恒成立(或).
若在定义域内存在最小值,则(或恒成立(或.
典型例题
典例2、(2)已知关于的不等式对一切实数恒成立,则实数的取值范围为______________.
解析
(2)讨论不等式二次项系数,结合判别式即可解答.具体解题过程如下:
①当,即或时,
显然符合条件,不符合条件.
②当时,由二次函数对一切实数恒为正数,得
解得.
结合①②得实数的取值范围是.
数学运算
一元二次不等式在给定区间上恒成立问题
综合问题解决能力
1.两根与的大小比较
一元二次不等式在给定区间上恒成立问题
综合问题解决能力
2.根在区间上的分布
典型例题
典例3-1[数学运算](2019-湖北武汉外校月考)关于的一元二次方程在区间上有实数解,求实数的取值范围.
点拨
本题为一元二次不等式的含参问题,求解此题,根据一元二次方程根的分布情况推出大致图象,借助根与系数的关系即可解答.
数学运算
典型例题
典例3-1[数学运算](2019-湖北武汉外校月考)关于的一元二次方程在区间上有实数解,求实数的取值范围.
解析
设,若在区间上有一个实数解,
∵或解得.若在区间上有两个实数解,
综上,可知的取值范围是.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
点拨
本题结合一元二次方程根的分布情况画出图象.利用数形结合思想解答问题.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
解析
(1)方法一:设函数,作其草图,如右图,
若两实根均大于1,
需即解得.
数学运算
典型例题
典例3-2已知方程有两实根.
(1)如果两实根都大于1,求实数的取值范围;
(2)如果两实根都在区间内,求实数的取值范围;
(3)如果一个根大于2,另一个根小于2,求实数的取值范围.
解析
(2)若两根,则所以.
(3)若一根大于2,另一根小于2,则,即0,解得.
数学运算
三个“二次”之间的关系的应用
分析计算能力
在解决具体的数学问题时,要注意一元二次不等式及相应的函数与方程三者之间的相互联系,并在一定条件下相互转化.
(1)若一元二次不等式的解集为区间的形式,则区间的端点值恰是相应一元二次方程的根,要注意解集与二次项数的联系.
(2)若已知一元二次方程的根,可以写出相应不等式的解集,反之,已知不等式的解集也可以写出相应二次方程的根,进一步可求得方程中的系数或得到系数之间的关系.
三个“二次”之间的关系的应用
分析计算能力
(3)二次函数与一元二次方程、一元二次不等式三者之间有紧密的关联.一元二次不等式的解集就是二次函数的图象中在轴上方的点的横坐标的集合,一元二次方程的根就是相应二次函数的图象与轴交点的横坐标.
典型例题
典例4(2019-陕西西安一中月考)若不等式的解集是,求不等式的解集.
数学运算
点拨
分析题意可发现要求不等式的解集,
先计算与其相应的一元二次方程的根,注意确定根与系数之间的关系.
典型例题
典例4(2019-陕西西安一中月考)若不等式的解集是,求不等式的解集.
数学运算
解析
由的解集为,知.
又,知.又为方程0的两个根,
∴.又,
∴不等式变为,即.
又∵,所求不等式的解集为.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
