高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式的关系》知识探究课件(共17张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式的关系》知识探究课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 20:16:55 | ||
图片预览






文档简介
(共17张PPT)
人教A版同步教材名师课件
二次函数与一元二次方程、不等式的关系
---知识探究
1.一元二次不等式:一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式,一元二次不等式的一般形式是或,其中均为常数,.
知识探究
探究点1 基本不等式
要点辨析
(1)一元二次不等式中的“一元”是指不等式中所要求解的未知数,并且这个未知数是唯一的,但这并不意味着不等式中不能含有其他字母,若含有其他字母,则把其他字母看成常数.
(2)一元二次不等式中的“二次”是指所要求解的未知数的最高次数必须是2,且最高次项的系数不为.
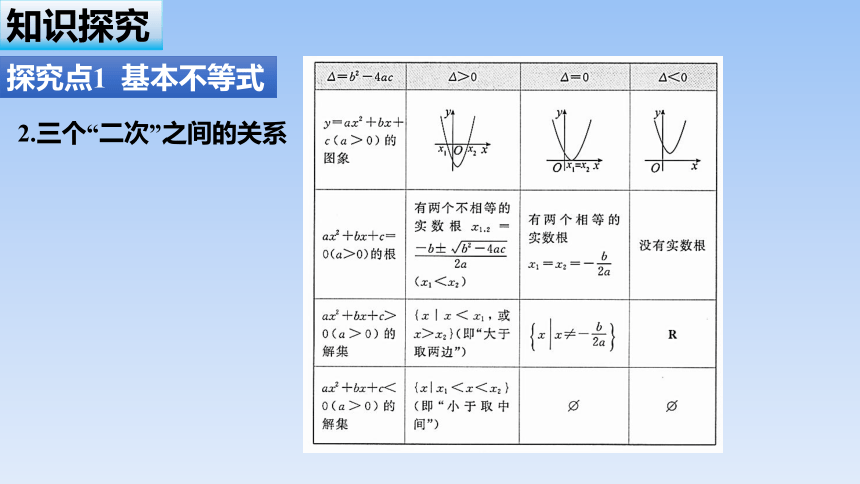
2.三个“二次”之间的关系
知识探究
探究点1 基本不等式
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
点拨
观察记忆能力
本题主要考查三个“二次”之间的联系,通过观察对应函数的图象求解一元二次不等式.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(1)作出函数图象,如下图所示,由图可知:
当时,或;
当时,或;
当时,.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(2)作出函数的图象,如下图所示,由图可知:
当时,;
当时,;
当时,符合题意的不存在.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(3)作出函数的图象,如下图所示,由图可知:
当时,;
当时,符合题意的不存在;
当时,符合题意的不存在.
1.求解一元二次不等式可利用相应的一元二次函数和数形结合的思想求解
2.一元二次不等式包括分式不等式,解分式不等式的原则是利用不等式的同解原理将其转化为有理整式不等式(组)求解,即
(1).
(2)支.
知识探究
探究点2 一元二次不等式的解法
(3)支.
(4)支.
(5)支.
对于的分式不等式,其中,先把不等式右边化为0,再通过商的符号法则,把它转化为整式不等式求解.
知识探究
探究点2 一元二次不等式的解法
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(1)因为,
所以方程有两个不等实根.
又二次函数的图象开口向上,
所以原不等式的解集为或.
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(2)因为,
所以方程有两个不等实根.又二次函数的图象开口向下,
所以原不等式的解集为.
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(3)原不等式可化为
即故原不等式的解集为.
将实际问题转化成不等式的数学模型是解决一元二次不等式应用问题的关键.
(1)将实际的不等关系写成对应的不等式时,应注意实际问题中关键性的文字语言与对应的数学符号之间的正确转换.
(2)掌握常见的文字语言与数学符号之间的对应关系.
知识探究
探究点3 一元二次不等式的应用
要点辨析
求解不等式应用题的四个步骤:
(1)审题,把握题干中的关键量,找准不等关系.(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型.
(3)解不等式,得出结论,注意数学模型中自变量的实际意义
(4)还原为实际问题的结果
典例3、汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停止.我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.
在一个限速为的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超过,乙车的刹车距离略超过.已知甲、乙两种车型的刹车距离与车速之间分别有如下关系:.问:甲、乙两车有无超速现象
典型例题
简单问题解决能力
典型例题
简单问题解决能力
解析
由题意知,对于甲车,有,即,解得或(不符合实际意义,舍去).这表明甲车的车速超过.
但根据题意知刹车距离略超过,由此估计甲车的车速不会超过限速.
对于乙车,有,即0.解得或(不符合实际意义,舍去),这表明乙车的车速超过,即超过规定限速.
点拨
找出问题中的不等关系建立数学模型是解决问题的关键.
人教A版同步教材名师课件
二次函数与一元二次方程、不等式的关系
---知识探究
1.一元二次不等式:一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式,一元二次不等式的一般形式是或,其中均为常数,.
知识探究
探究点1 基本不等式
要点辨析
(1)一元二次不等式中的“一元”是指不等式中所要求解的未知数,并且这个未知数是唯一的,但这并不意味着不等式中不能含有其他字母,若含有其他字母,则把其他字母看成常数.
(2)一元二次不等式中的“二次”是指所要求解的未知数的最高次数必须是2,且最高次项的系数不为.
2.三个“二次”之间的关系
知识探究
探究点1 基本不等式
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
点拨
观察记忆能力
本题主要考查三个“二次”之间的联系,通过观察对应函数的图象求解一元二次不等式.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(1)作出函数图象,如下图所示,由图可知:
当时,或;
当时,或;
当时,.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(2)作出函数的图象,如下图所示,由图可知:
当时,;
当时,;
当时,符合题意的不存在.
典例1、(2019-山东青岛二中周练)分别画出下列函数的图象,并分别指出函数值,时,自变量的取值.
(1). (2). (3).
典型例题
解析
观察记忆能力
(3)作出函数的图象,如下图所示,由图可知:
当时,;
当时,符合题意的不存在;
当时,符合题意的不存在.
1.求解一元二次不等式可利用相应的一元二次函数和数形结合的思想求解
2.一元二次不等式包括分式不等式,解分式不等式的原则是利用不等式的同解原理将其转化为有理整式不等式(组)求解,即
(1).
(2)支.
知识探究
探究点2 一元二次不等式的解法
(3)支.
(4)支.
(5)支.
对于的分式不等式,其中,先把不等式右边化为0,再通过商的符号法则,把它转化为整式不等式求解.
知识探究
探究点2 一元二次不等式的解法
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(1)因为,
所以方程有两个不等实根.
又二次函数的图象开口向上,
所以原不等式的解集为或.
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(2)因为,
所以方程有两个不等实根.又二次函数的图象开口向下,
所以原不等式的解集为.
典例2.[分析计算能力]解下列不等式:
典型例题
解析
概括理解能力
(3)原不等式可化为
即故原不等式的解集为.
将实际问题转化成不等式的数学模型是解决一元二次不等式应用问题的关键.
(1)将实际的不等关系写成对应的不等式时,应注意实际问题中关键性的文字语言与对应的数学符号之间的正确转换.
(2)掌握常见的文字语言与数学符号之间的对应关系.
知识探究
探究点3 一元二次不等式的应用
要点辨析
求解不等式应用题的四个步骤:
(1)审题,把握题干中的关键量,找准不等关系.(2)引进数学符号,将文字信息转化为符号语言,用不等式表示不等关系,建立相应的数学模型.
(3)解不等式,得出结论,注意数学模型中自变量的实际意义
(4)还原为实际问题的结果
典例3、汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停止.我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.
在一个限速为的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超过,乙车的刹车距离略超过.已知甲、乙两种车型的刹车距离与车速之间分别有如下关系:.问:甲、乙两车有无超速现象
典型例题
简单问题解决能力
典型例题
简单问题解决能力
解析
由题意知,对于甲车,有,即,解得或(不符合实际意义,舍去).这表明甲车的车速超过.
但根据题意知刹车距离略超过,由此估计甲车的车速不会超过限速.
对于乙车,有,即0.解得或(不符合实际意义,舍去),这表明乙车的车速超过,即超过规定限速.
点拨
找出问题中的不等关系建立数学模型是解决问题的关键.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
