高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式---第二课时》名师课件(共20张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式---第二课时》名师课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 20:10:51 | ||
图片预览







文档简介
(共20张PPT)
解一元二次不等式的步骤
(1)化成标准形式或 <0();
(2) 因式分解,不能因式分解的判断判别式△与0的关系,求出相应一元二次方程的实根;
(3)画出对应函数的草图;
(4)写出不等式的解集.
(大于取两根之外,小于取两根之间)
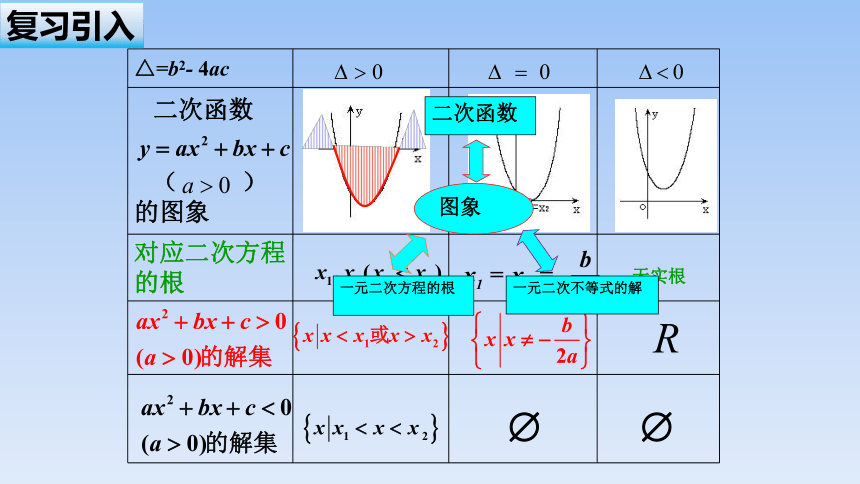
复习引入
△=b2- 4ac
二次函数 ( )的图象
对应二次方程的根
无实根
二次函数
一元二次方程的根
一元二次不等式的解
图象
复习引入
人教A版同步教材名师课件
二次函数与一元二次方程、不等式
---第二课时
分式、含参的一元二次不等式的解法等
学习目标
学 习 目 标 核心素养
体会从实际情境中抽象出一元二次不等式的过程 数学抽象
通过函数图象了解一元二次不等式与相应函数、方程的联系 直观想象
会解一元二次不等式. 数学运算
能够利用一元二次不等式解决一些实际问题. 数学建模
像(1)、 (2)、 (3)这样的不等式叫做含参数的一元二次不等式;而像(4)、 (5) 这样的不等式叫做简单分数不等式
探究新知
观察:
(1) ;
(2);
(3);
(4)≥0;
(5) >1.
典例讲解
例1.
解析
1
a
二算
三求
四画
五写
例2.解关于x的不等式(ax-1)(x+1)>0.
若a=0,则原不等式为一元一次不等式,解集为(-∞,-1).
当a≠0时,方程(ax-1)(x+1)=0的两根为x1=,x2=-1.
当a>0时,解集为(-∞,-1)∪(,+∞);
当-1当a<-1,即0> >-1时,解集为;
当a=-1时,解集为 .
典例讲解
解析
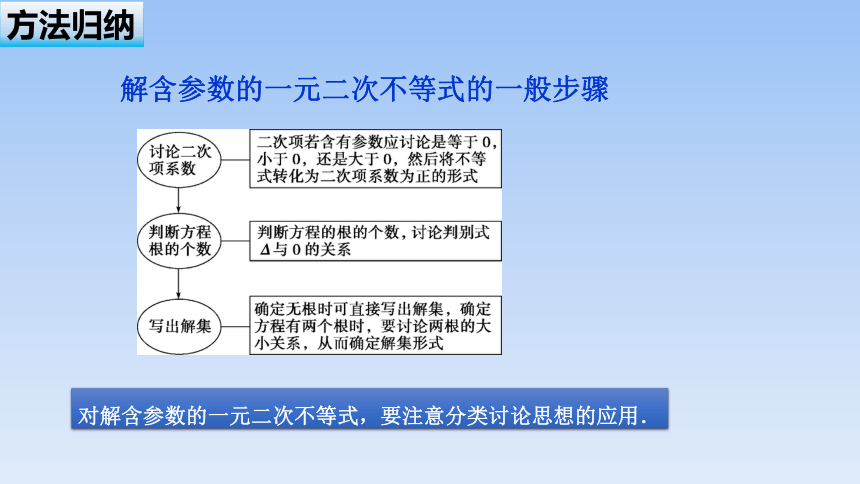
方法归纳
解含参数的一元二次不等式的一般步骤
对解含参数的一元二次不等式,要注意分类讨论思想的应用.
变式训练
1.解关于x的不等式:ax2-(a+1)x+1<0.(a∈R,a>0)
解:因为a>0,原不等式等价于()(x-1)<0.
①当a=1时,=1, ()(x-1)<0无解;
②当a>1时,<1,解()(x-1)<0 ,得③当01,解()(x-1)<0 ,得1综上所述,
当0当a=1时,原不等式的解集为 ;
当a>1时,原不等式的解集为{x |例3.解下列不等式
(1)≥0;(2) >1.
(1)因为≥0 x<或x≥ .
所以原不等式的解集为.
(2)原不等式可化为或 或典例讲解
解析
方法归纳
先通过移项、通分整理成标准型>0(<0)或≥0(≤0),再化成整式不等式(组)来解.如果能判断出分母的正负,直接去分母即可.
分式不等式的解法
变式训练
解析:(1)原不等式等价于3≤0 ≤0 ≥0 x(2x-1)≥0, 且x≠0,解得x≥ 或x<0.
2.(1)不等式≤3的解集是________.
(2)不等式>1的解集是________.
{x|x≥或x<0}
{x| x<-3或x>4}
(2)原不等式等价于-1>0,即>0 (x-4)(x+3)>0 x<-3或x>4.
典例讲解
例4.某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x≠0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
(1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.依题意得y=200a(1+2x%)(10-x)%=a(100+2x)(10-x)(0(2)原计划税收为200a×10%=20a(万元).依题意得a(100+2x)(10-x)≥20a×83.2%,化简得x2+40x-84≤0,解得-42≤x≤2.又因为0解析
方法归纳
(1)阅读理解、认真审题,把握问题中的关键量、找准不等关系.
(2)引入数学符号,用不等式表示不等关系(或表示成函数关系).
(3)解不等式(或求函数最值).
(4)回扣实际问题.
解不等式应用题的四个步骤
变式训练
3.某校园内有一块长为800 m,宽为600 m的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,如图,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围.
解:设花卉带宽度为x m,则草坪的长为(800-2x)m,宽为(600-2x)m,
根据题意,得(800-2x)(600-2x)≥×800×600,
整理,得x2-700x+60 000≥0,解得x≥600(舍去)或x≤100,
由题意知x>0,所以0即当花卉带的宽度在(0,100]内取值时,草坪的面积不小于总面积的一半.
素养提炼
1.解含参数的一元二次型的不等式易误点
(1)若二次项系数含参数,易忽视二次项系数为0的情况.
(2)对参数进行分类讨论,易出现重复、遗漏现象.
(3)关于不等式对应的方程根的讨论:二根(Δ>0),一根(Δ=0),无根(Δ<0).
素养提炼
2.分式不等式转化为整式不等式的常见方法
(1) >0 f(x)g(x)>0,
(2)<0 f(x)g(x)<0,
(3)≥0
(4)≤0
(3)(4)转化为整式不等式时要注意分母不为0.
当堂练习
1.不等式>0的解集是( )
A.{x|-2-1}
C.{x|x<-3或x>-2} D.{x|x<-2或x>-1}
解析:不等式>0等价于(x+1)(x+2)>0,所以不等式的解集是{x|x<-2或x>-1}.
D
2.若不等式x2+mx+>0的解集为R,则实数m的取值范围是( )
A.(2,+∞) B.(-∞,2)
C.(-∞,0)∪(2,+∞) D.(0,2)
解析:由题意知原不等式对应方程的Δ<0,即m2-4×1×<0,即m2-2m<0,解得0D
当堂练习
3.某小型服装厂生产一种风衣,日销售量x件与售价P元/件之间的关系为P=150-2x,生产x件所需成本为C=50+30x元,要使日获利不少于1 300元,则该厂日产量应在_____________________范围之内(件).
解析:由题意得:(150-2x)x-(50+30x)≥1 300,
化简得:x2-60x+675≤0,解得15≤x≤45,且x为整数.
{x|15≤x≤45,x∈N*}
当堂练习
4.解不等式<0
解:<0,即ax(x+1)<0.
当a>0时,ax(x+1)<0,所以x(x+1)<0,解得{x|-1当a=0时,原不等式的解集为 ;
当a<0时,ax(x+1)<0,
所以x(x+1)>0,解得{x|x>0或x<-1}.
综上,当a>0时,原不等式的解集为{x|-1当a=0时,原不等式的解集为 ;
当a<0时,原不等式的解集为{x|x>0或x<-1}.
解一元二次不等式的步骤
(1)化成标准形式或 <0();
(2) 因式分解,不能因式分解的判断判别式△与0的关系,求出相应一元二次方程的实根;
(3)画出对应函数的草图;
(4)写出不等式的解集.
(大于取两根之外,小于取两根之间)
复习引入
△=b2- 4ac
二次函数 ( )的图象
对应二次方程的根
无实根
二次函数
一元二次方程的根
一元二次不等式的解
图象
复习引入
人教A版同步教材名师课件
二次函数与一元二次方程、不等式
---第二课时
分式、含参的一元二次不等式的解法等
学习目标
学 习 目 标 核心素养
体会从实际情境中抽象出一元二次不等式的过程 数学抽象
通过函数图象了解一元二次不等式与相应函数、方程的联系 直观想象
会解一元二次不等式. 数学运算
能够利用一元二次不等式解决一些实际问题. 数学建模
像(1)、 (2)、 (3)这样的不等式叫做含参数的一元二次不等式;而像(4)、 (5) 这样的不等式叫做简单分数不等式
探究新知
观察:
(1) ;
(2);
(3);
(4)≥0;
(5) >1.
典例讲解
例1.
解析
1
a
二算
三求
四画
五写
例2.解关于x的不等式(ax-1)(x+1)>0.
若a=0,则原不等式为一元一次不等式,解集为(-∞,-1).
当a≠0时,方程(ax-1)(x+1)=0的两根为x1=,x2=-1.
当a>0时,解集为(-∞,-1)∪(,+∞);
当-1
当a=-1时,解集为 .
典例讲解
解析
方法归纳
解含参数的一元二次不等式的一般步骤
对解含参数的一元二次不等式,要注意分类讨论思想的应用.
变式训练
1.解关于x的不等式:ax2-(a+1)x+1<0.(a∈R,a>0)
解:因为a>0,原不等式等价于()(x-1)<0.
①当a=1时,=1, ()(x-1)<0无解;
②当a>1时,<1,解()(x-1)<0 ,得
当0
当a>1时,原不等式的解集为{x |
(1)≥0;(2) >1.
(1)因为≥0 x<或x≥ .
所以原不等式的解集为.
(2)原不等式可化为或 或
解析
方法归纳
先通过移项、通分整理成标准型>0(<0)或≥0(≤0),再化成整式不等式(组)来解.如果能判断出分母的正负,直接去分母即可.
分式不等式的解法
变式训练
解析:(1)原不等式等价于3≤0 ≤0 ≥0 x(2x-1)≥0, 且x≠0,解得x≥ 或x<0.
2.(1)不等式≤3的解集是________.
(2)不等式>1的解集是________.
{x|x≥或x<0}
{x| x<-3或x>4}
(2)原不等式等价于-1>0,即>0 (x-4)(x+3)>0 x<-3或x>4.
典例讲解
例4.某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担,政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x≠0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
(1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.依题意得y=200a(1+2x%)(10-x)%=a(100+2x)(10-x)(0
方法归纳
(1)阅读理解、认真审题,把握问题中的关键量、找准不等关系.
(2)引入数学符号,用不等式表示不等关系(或表示成函数关系).
(3)解不等式(或求函数最值).
(4)回扣实际问题.
解不等式应用题的四个步骤
变式训练
3.某校园内有一块长为800 m,宽为600 m的长方形地面,现要对该地面进行绿化,规划四周种花卉(花卉带的宽度相同),中间种草坪,如图,若要求草坪的面积不小于总面积的一半,求花卉带宽度的范围.
解:设花卉带宽度为x m,则草坪的长为(800-2x)m,宽为(600-2x)m,
根据题意,得(800-2x)(600-2x)≥×800×600,
整理,得x2-700x+60 000≥0,解得x≥600(舍去)或x≤100,
由题意知x>0,所以0
素养提炼
1.解含参数的一元二次型的不等式易误点
(1)若二次项系数含参数,易忽视二次项系数为0的情况.
(2)对参数进行分类讨论,易出现重复、遗漏现象.
(3)关于不等式对应的方程根的讨论:二根(Δ>0),一根(Δ=0),无根(Δ<0).
素养提炼
2.分式不等式转化为整式不等式的常见方法
(1) >0 f(x)g(x)>0,
(2)<0 f(x)g(x)<0,
(3)≥0
(4)≤0
(3)(4)转化为整式不等式时要注意分母不为0.
当堂练习
1.不等式>0的解集是( )
A.{x|-2
C.{x|x<-3或x>-2} D.{x|x<-2或x>-1}
解析:不等式>0等价于(x+1)(x+2)>0,所以不等式的解集是{x|x<-2或x>-1}.
D
2.若不等式x2+mx+>0的解集为R,则实数m的取值范围是( )
A.(2,+∞) B.(-∞,2)
C.(-∞,0)∪(2,+∞) D.(0,2)
解析:由题意知原不等式对应方程的Δ<0,即m2-4×1×<0,即m2-2m<0,解得0
当堂练习
3.某小型服装厂生产一种风衣,日销售量x件与售价P元/件之间的关系为P=150-2x,生产x件所需成本为C=50+30x元,要使日获利不少于1 300元,则该厂日产量应在_____________________范围之内(件).
解析:由题意得:(150-2x)x-(50+30x)≥1 300,
化简得:x2-60x+675≤0,解得15≤x≤45,且x为整数.
{x|15≤x≤45,x∈N*}
当堂练习
4.解不等式<0
解:<0,即ax(x+1)<0.
当a>0时,ax(x+1)<0,所以x(x+1)<0,解得{x|-1
当a<0时,ax(x+1)<0,
所以x(x+1)>0,解得{x|x>0或x<-1}.
综上,当a>0时,原不等式的解集为{x|-1
当a<0时,原不等式的解集为{x|x>0或x<-1}.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
