高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式---第一课时》名师课件(共23张PPT)
文档属性
| 名称 | 高中数学必修第一册人教A版《2.3二次函数与一元二次方程、不等式---第一课时》名师课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 20:11:40 | ||
图片预览








文档简介
(共23张PPT)
复习引入
在初中,我们从一次函数的角度看一元一次方程、一元一次不等式,发现了三者之间的内在联系,利用这种联系可以更好地解决相关问题,对于二次函数、一元二次方程和一元二次不等式,是否也有这样的联系呢?
人教A版同步教材名师课件
二次函数与一元二次方程、不等式
---第一课时
学习目标
学 习 目 标 核心素养
体会从实际情境中抽象出一元二次不等式的过程 数学抽象
通过函数图象了解一元二次不等式与相应函数、方程的联系 直观想象
会解一元二次不等式. 数学运算
能够利用一元二次不等式解决一些实际问题. 数学建模
课程目标
1. 通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系.
2. 使学生能够运用二次函数及其图像,性质解决实际问题.
3. 渗透数形结合思想,进一步培养学生综合解题能力。
数学学科素养
1.数学抽象:一元二次函数与一元二次方程,一元二次不等式之间的联系;
2.逻辑推理:一元二次不等式恒成立问题;
3.数学运算:解一元二次不等式;
4.数据分析:一元二次不等式解决实际问题;
5.数学建模:运用数形结合的思想,逐步渗透一元二次函数与一元二次方程,一元二次不等式之间的联系.
学习目标
探究新知
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉,若栅栏的长度是24 m,围成的矩形区域的面积要大于20 ,则这个矩形的边长为多少米?
设这个矩形的一条边长为,则另一条边长为.由题意,得 ,其中.
整理得 . ①
求得不等式①的解集,就得到了问题的答案.
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式(quadric inequality in one unknown).一元二次不等式的一般形式是或,其中均为常数, .
画出函数的图象,并根据图象回答:
(1).图象与轴交点的坐标为 ,该坐标与方程的解有什么关系: .
(2).当取 时, =0?
当取 时, >0?
当取 时, <0?
(2, 0),(10, 0)
交点的横坐标即为方程的根
= 2 或 10
<2 或 >10
2 < <10
y
0
2
10
o
o
o
o
>0
>0
<0
探究新知
(3).由图象写出:
不等式>0的解集
为 .
不等式的解集为 .
{|<2 或 >10}
{| 2 < <10}
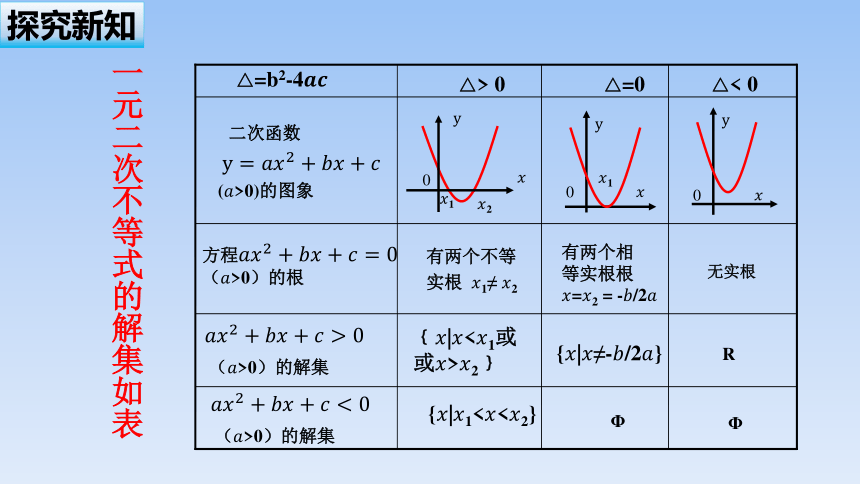
一元二次不等式的解集如表
△=b2-4
△> 0
△=0
△< 0
二次函数
(>0)的图象
方程 (>0)的根
(>0)的解集
(>0)的解集
有两个不等
实根 1≠ 2
有两个相
等实根根
=2 = -/2
无实根
﹛|<1或
或>2﹜
{|≠-/2}
R
{|1<<2}
Φ
Φ
0
1
0
1
2
0
探究新知
解一元二次不等式的方法步骤是:
(3)根据图象写出解集.
步骤:(1)化成标准形式 (>0):
或 ax2+bx+c<0;
(2)求△,解方程,画图象;
方法:数形结合
探究新知
例1:解不等式:
∵ △=
方程=0的两根为:
=-3,或=5
y
-3
5
0
x
∴ 不等式的解集为:{ ≤-3 或 ≥5}.
。
。
典例讲解
解析
方法归纳
(1)通过对不等式变形,使二次项系数大于零;
(2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据判别式说明方程有没有实根;
(4)根据函数图象与x轴的相关位置写出不等式的解集.
解一元二次不等式的一般步骤
变式训练
1.解下列不等式:
(1)2x2-3x-2>0;(2)x2-3x+5>0;(3)-4x2≥1-4x.
解:(1)因为Δ=(-3)2-4×2×(-2)=25>0,所以方程2x2-3x-2=0的两根为-,2,再根据函数y=2x2-3x-2的图象开口方向,所以原不等式的解集为.
(2)因为Δ=(-3)2-4×1×5=-11<0,再根据函数y=x2-3x+5图象的开口方向,
所以原不等式的解集为R.
(3)原不等式可化为4x2-4x+1≤0.因为Δ=(-4)2-4×4×1=0,方程4x2-4x+1=0的根为x=,所以原不等式的解集是{x | x=}.
例2. 已知一元二次不等式
的解集为{}, 求的值.
由题意知 : 且方程 的根是-2、3 , 代入方程可得:
则=-2
解方程组得:
典例讲解
根据根与系数关系得:
解析
(1)给出一元二次不等式的解集,则可知二次项系数的符号和相应一元二次方程的两根.
(2)三个二次的关系体现了数形结合,以及函数与方程的思想方法.
方法归纳
2.若关于的不等式 的解集是,则____
变式训练
解:由题意知 : 且方程 的根是, 代入方程可得:
则=-14
解方程组得:
根据根与系数关系得:
例3.设函数,若对于一切实数,恒成立,求的取值范围.
典例讲解
要使,
则有:
⑴当=0时,化为-1<0,恒成立,符合题意;
⑵当≠0时,则有, 解得.
解析
方法归纳
1.不等式ax2+bx+c>0的解是全体实数(或恒成立)的条件是当a=0时,b=0,c>0;当a≠0时, 不等式ax2+bx+c<0的解是全体实数(或恒成立)的条件是当a=0时,b=0,c<0;当a≠0时,
2.解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
3.对一切实数,关于的不等式 恒成立,求实数的取值范围.
解:要使,
则有:
⑴当=0时,化为<0,解得,不合题意;
⑵当≠0时,则有, 解得.
变式训练
素养提炼
1.解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0),或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m0,则可得x>n或x有口诀如下:大于取两边,小于取中间.
素养提炼
2.与不等式有关的恒成立问题的等价转化方式
(1)不等式ax2+bx+c>0的解是全体实数的条件是:
①当a=0时,b=0,c>0;
②当a≠0时,
(2)不等式ax2+bx+c<0的解是全体实数的条件是:
①当a=0时,b=0,c<0;
②当a≠0时,
对a是否为零要进行讨论.
当堂练习
1.不等式(3x-2)(2-x)≥0的解集是( )
A. B.∪[2,+∞)
C. D.
解析:原不等式等价于(x- )(x-2) ≤0,解得≤x≤2,故选A.
A
2.函数y=的定义域为( )
A.[-7,1] B.(-7,1)
C.(-∞,-7]∪[1,+∞) D.(-∞,-7)∪(1,+∞)
解析:由7-6x-x2>0,得x2+6x-7<0,即(x+7)(x-1)<0,所以-7B
当堂练习
3.已知方程ax2+bx+2=0的两根为和2.
(1)求a,b的值.
(2)解不等式ax2+bx-1>0.
解:(1)因为方程ax2+bx+2=0的两根为和2,
由根与系数的关系,得解得a=-2,b=3.
(2)由(1)知,ax2+bx-1>0变为-2x2+3x-1>0,即2x2-3x+1<0,解得0的解集为{归纳小结
⒉一元二次不等式的简单应用
⒈一元二次不等式的解法;
作 业
课本P53:练习:1
课本P58:综合运用:6
复习引入
在初中,我们从一次函数的角度看一元一次方程、一元一次不等式,发现了三者之间的内在联系,利用这种联系可以更好地解决相关问题,对于二次函数、一元二次方程和一元二次不等式,是否也有这样的联系呢?
人教A版同步教材名师课件
二次函数与一元二次方程、不等式
---第一课时
学习目标
学 习 目 标 核心素养
体会从实际情境中抽象出一元二次不等式的过程 数学抽象
通过函数图象了解一元二次不等式与相应函数、方程的联系 直观想象
会解一元二次不等式. 数学运算
能够利用一元二次不等式解决一些实际问题. 数学建模
课程目标
1. 通过探索,使学生理解二次函数与一元二次方程,一元二次不等式之间的联系.
2. 使学生能够运用二次函数及其图像,性质解决实际问题.
3. 渗透数形结合思想,进一步培养学生综合解题能力。
数学学科素养
1.数学抽象:一元二次函数与一元二次方程,一元二次不等式之间的联系;
2.逻辑推理:一元二次不等式恒成立问题;
3.数学运算:解一元二次不等式;
4.数据分析:一元二次不等式解决实际问题;
5.数学建模:运用数形结合的思想,逐步渗透一元二次函数与一元二次方程,一元二次不等式之间的联系.
学习目标
探究新知
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉,若栅栏的长度是24 m,围成的矩形区域的面积要大于20 ,则这个矩形的边长为多少米?
设这个矩形的一条边长为,则另一条边长为.由题意,得 ,其中.
整理得 . ①
求得不等式①的解集,就得到了问题的答案.
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式(quadric inequality in one unknown).一元二次不等式的一般形式是或,其中均为常数, .
画出函数的图象,并根据图象回答:
(1).图象与轴交点的坐标为 ,该坐标与方程的解有什么关系: .
(2).当取 时, =0?
当取 时, >0?
当取 时, <0?
(2, 0),(10, 0)
交点的横坐标即为方程的根
= 2 或 10
<2 或 >10
2 < <10
y
0
2
10
o
o
o
o
>0
>0
<0
探究新知
(3).由图象写出:
不等式>0的解集
为 .
不等式的解集为 .
{|<2 或 >10}
{| 2 < <10}
一元二次不等式的解集如表
△=b2-4
△> 0
△=0
△< 0
二次函数
(>0)的图象
方程 (>0)的根
(>0)的解集
(>0)的解集
有两个不等
实根 1≠ 2
有两个相
等实根根
=2 = -/2
无实根
﹛|<1或
或>2﹜
{|≠-/2}
R
{|1<<2}
Φ
Φ
0
1
0
1
2
0
探究新知
解一元二次不等式的方法步骤是:
(3)根据图象写出解集.
步骤:(1)化成标准形式 (>0):
或 ax2+bx+c<0;
(2)求△,解方程,画图象;
方法:数形结合
探究新知
例1:解不等式:
∵ △=
方程=0的两根为:
=-3,或=5
y
-3
5
0
x
∴ 不等式的解集为:{ ≤-3 或 ≥5}.
。
。
典例讲解
解析
方法归纳
(1)通过对不等式变形,使二次项系数大于零;
(2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据判别式说明方程有没有实根;
(4)根据函数图象与x轴的相关位置写出不等式的解集.
解一元二次不等式的一般步骤
变式训练
1.解下列不等式:
(1)2x2-3x-2>0;(2)x2-3x+5>0;(3)-4x2≥1-4x.
解:(1)因为Δ=(-3)2-4×2×(-2)=25>0,所以方程2x2-3x-2=0的两根为-,2,再根据函数y=2x2-3x-2的图象开口方向,所以原不等式的解集为.
(2)因为Δ=(-3)2-4×1×5=-11<0,再根据函数y=x2-3x+5图象的开口方向,
所以原不等式的解集为R.
(3)原不等式可化为4x2-4x+1≤0.因为Δ=(-4)2-4×4×1=0,方程4x2-4x+1=0的根为x=,所以原不等式的解集是{x | x=}.
例2. 已知一元二次不等式
的解集为{}, 求的值.
由题意知 : 且方程 的根是-2、3 , 代入方程可得:
则=-2
解方程组得:
典例讲解
根据根与系数关系得:
解析
(1)给出一元二次不等式的解集,则可知二次项系数的符号和相应一元二次方程的两根.
(2)三个二次的关系体现了数形结合,以及函数与方程的思想方法.
方法归纳
2.若关于的不等式 的解集是,则____
变式训练
解:由题意知 : 且方程 的根是, 代入方程可得:
则=-14
解方程组得:
根据根与系数关系得:
例3.设函数,若对于一切实数,恒成立,求的取值范围.
典例讲解
要使,
则有:
⑴当=0时,化为-1<0,恒成立,符合题意;
⑵当≠0时,则有, 解得.
解析
方法归纳
1.不等式ax2+bx+c>0的解是全体实数(或恒成立)的条件是当a=0时,b=0,c>0;当a≠0时, 不等式ax2+bx+c<0的解是全体实数(或恒成立)的条件是当a=0时,b=0,c<0;当a≠0时,
2.解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
3.对一切实数,关于的不等式 恒成立,求实数的取值范围.
解:要使,
则有:
⑴当=0时,化为<0,解得,不合题意;
⑵当≠0时,则有, 解得.
变式训练
素养提炼
1.解一元二次不等式的常见方法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0),或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m
素养提炼
2.与不等式有关的恒成立问题的等价转化方式
(1)不等式ax2+bx+c>0的解是全体实数的条件是:
①当a=0时,b=0,c>0;
②当a≠0时,
(2)不等式ax2+bx+c<0的解是全体实数的条件是:
①当a=0时,b=0,c<0;
②当a≠0时,
对a是否为零要进行讨论.
当堂练习
1.不等式(3x-2)(2-x)≥0的解集是( )
A. B.∪[2,+∞)
C. D.
解析:原不等式等价于(x- )(x-2) ≤0,解得≤x≤2,故选A.
A
2.函数y=的定义域为( )
A.[-7,1] B.(-7,1)
C.(-∞,-7]∪[1,+∞) D.(-∞,-7)∪(1,+∞)
解析:由7-6x-x2>0,得x2+6x-7<0,即(x+7)(x-1)<0,所以-7
当堂练习
3.已知方程ax2+bx+2=0的两根为和2.
(1)求a,b的值.
(2)解不等式ax2+bx-1>0.
解:(1)因为方程ax2+bx+2=0的两根为和2,
由根与系数的关系,得解得a=-2,b=3.
(2)由(1)知,ax2+bx-1>0变为-2x2+3x-1>0,即2x2-3x+1<0,解得
⒉一元二次不等式的简单应用
⒈一元二次不等式的解法;
作 业
课本P53:练习:1
课本P58:综合运用:6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
