浙教版小学数学五年级上册4.15《组合图形的面积》练习题(含答案)
文档属性
| 名称 | 浙教版小学数学五年级上册4.15《组合图形的面积》练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 140.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-31 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版五年级上册数学组合图形的面积练习题(附答案)
一、单选题
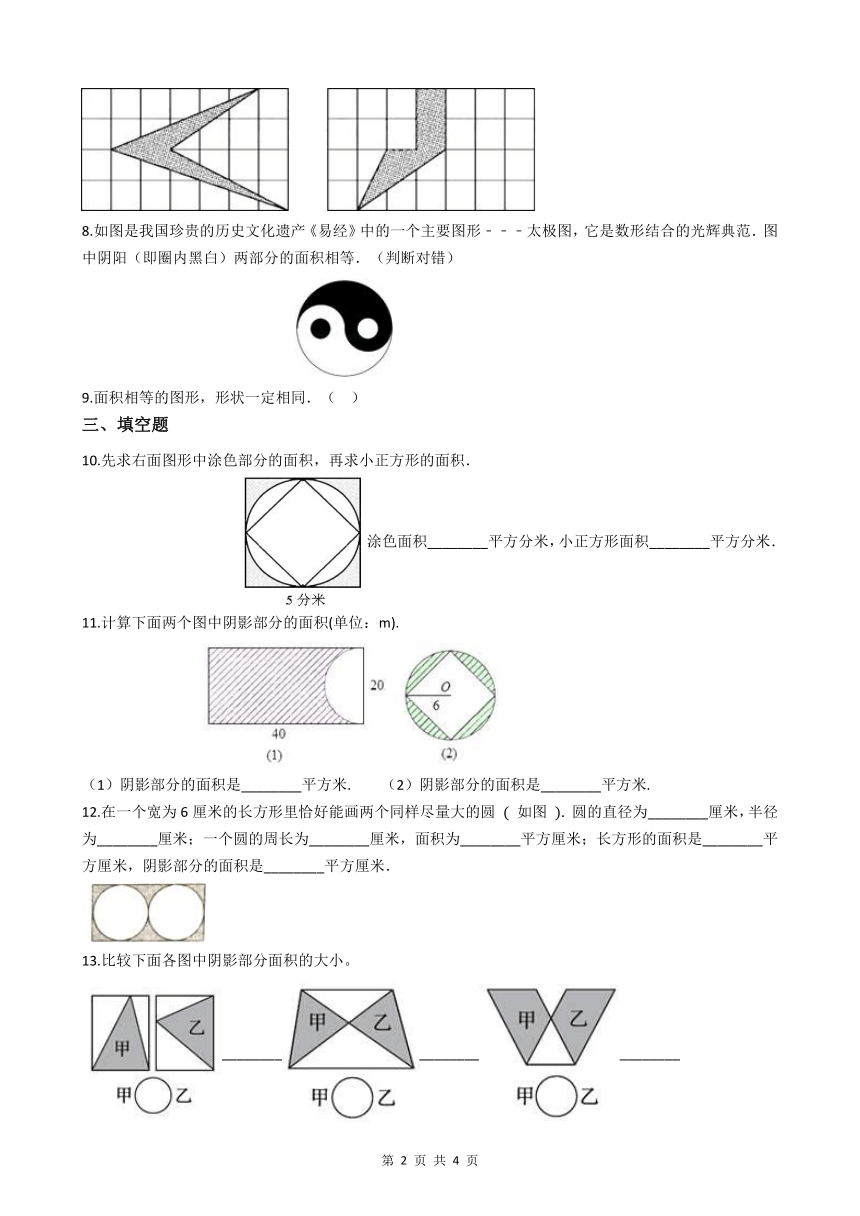
1.在如图梯形中,两个阴影部分的面积相比( )
A. 甲大于乙 B. 乙大于甲 C. 甲等于乙 D. 无法比较
2.图中两个正方形完全相同,阴影部分面积比较,( )
A. 相等 B. A的阴影部分面积大 C. B的阴影部分面积大 D. 无法确定
3.把一个长方形沿虚线剪成两块(如图),这两个图形( )。
A. 周长相等,面积相等 B. 周长相等,面积不等
C. 周长不相等,面积相等 D. 周长不相等,面积不相等
4.每个口代表1平方厘米,下面三个图形中,面积最大的是( )。
A. B. C.
5.两个完全一样的直角三角形重叠成右图形状,形成两个梯形,这两个梯形的面积大小关系是( )。
A. A大 B. B大 C. 相等 D. 无法确定
二、判断题
6.用同样的小方块拼成 和 ,它们的表面积相等。( )
7.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
8.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)
9.面积相等的图形,形状一定相同.( )
三、填空题
10.先求右面图形中涂色部分的面积,再求小正方形的面积.
涂色面积________平方分米,小正方形面积________平方分米.
11.计算下面两个图中阴影部分的面积(单位:m).
(1)阴影部分的面积是________平方米. (2)阴影部分的面积是________平方米.
12.在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆 如图 圆的直径为________厘米,半径为________厘米;一个圆的周长为________厘米,面积为________平方厘米;长方形的面积是________平方厘米,阴影部分的面积是________平方厘米.
13.比较下面各图中阴影部分面积的大小。
________________________
14.如图是用边长1厘米的小正方形拼成的,它的周长是________厘米,面积是________平方厘米.
四、计算题
15.求图中阴影部分的面积.(单位:厘米)注:正方形对角线是8.
16.如图,阴影部分①比阴影部分②的面积多多少?(单位:厘米)
五、解答题
17.求下面图形阴影部分的周长和面积。(单位:分米)
18.计算下面图形的面积。
六、应用题
19.边长分别为4cm和6cm的两个正方形拼在一起(如下图),阴影部分的面积是多少平方厘米?
20.求图中阴影部分的面积.(单位:厘米)
答 案
一、单选题
1. C 2. A 3. B 4. B 5. C
二、判断题
6. 正确 7. 正确 8. 正确 9. 错误
三、填空题
10. 5.375;12.5 11. (1)643(2)41.04
12. 6;3;18.84;28.26;72;15.48 13. =;=;= 14. 12;5
四、计算题
15. 解:8÷2=4(厘米),
4×4÷2×4,=16÷2×4,=8×4,=32(平方厘米);
答:阴影部分的面积是32平方厘米
16. 解:6×4÷2﹣3.14×62× , =24÷2﹣3.14×36× ,=12﹣9.42,=2.58(平方厘米);
答:阴影部分①比阴影部分②的面积多2.58平方厘米
五、解答题
17. 解:(3+6)×2-5+3.14×5÷2
=18-5+7.85=13+7.85=20.85(分米)
3×6-(5÷2)2×3.14÷2
=18-2.5×2.5×3.14÷2=18-9.8125=8.1875(平方分米)
18. 解:30×30+30×25=900+750 =1650(cm2)
六、应用题
19. 解:阴影部分面积为
答:阴影部分的面积是14平方厘米.
20. 解:[(5+8+5)×5÷2﹣ ×3.14×52]+( ×3.14×52﹣5×5÷2),
=[18×5÷2﹣0.785×25]+(0.785×25﹣25÷2),
=[90÷2﹣19.625]+(19.625﹣12.5),
=[45﹣19.625]+7.125,
=25.375+7.125,
=32.5(平方厘米);
答:阴影部分的面积为32.5平方厘米
(
第
1
页 共
6
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
浙教版五年级上册数学组合图形的面积练习题(附答案)
一、单选题
1.在如图梯形中,两个阴影部分的面积相比( )
A. 甲大于乙 B. 乙大于甲 C. 甲等于乙 D. 无法比较
2.图中两个正方形完全相同,阴影部分面积比较,( )
A. 相等 B. A的阴影部分面积大 C. B的阴影部分面积大 D. 无法确定
3.把一个长方形沿虚线剪成两块(如图),这两个图形( )。
A. 周长相等,面积相等 B. 周长相等,面积不等
C. 周长不相等,面积相等 D. 周长不相等,面积不相等
4.每个口代表1平方厘米,下面三个图形中,面积最大的是( )。
A. B. C.
5.两个完全一样的直角三角形重叠成右图形状,形成两个梯形,这两个梯形的面积大小关系是( )。
A. A大 B. B大 C. 相等 D. 无法确定
二、判断题
6.用同样的小方块拼成 和 ,它们的表面积相等。( )
7.下面两图中阴影部分的面积相等。(每个小方格的边长表示1cm)
8.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)
9.面积相等的图形,形状一定相同.( )
三、填空题
10.先求右面图形中涂色部分的面积,再求小正方形的面积.
涂色面积________平方分米,小正方形面积________平方分米.
11.计算下面两个图中阴影部分的面积(单位:m).
(1)阴影部分的面积是________平方米. (2)阴影部分的面积是________平方米.
12.在一个宽为6厘米的长方形里恰好能画两个同样尽量大的圆 如图 圆的直径为________厘米,半径为________厘米;一个圆的周长为________厘米,面积为________平方厘米;长方形的面积是________平方厘米,阴影部分的面积是________平方厘米.
13.比较下面各图中阴影部分面积的大小。
________________________
14.如图是用边长1厘米的小正方形拼成的,它的周长是________厘米,面积是________平方厘米.
四、计算题
15.求图中阴影部分的面积.(单位:厘米)注:正方形对角线是8.
16.如图,阴影部分①比阴影部分②的面积多多少?(单位:厘米)
五、解答题
17.求下面图形阴影部分的周长和面积。(单位:分米)
18.计算下面图形的面积。
六、应用题
19.边长分别为4cm和6cm的两个正方形拼在一起(如下图),阴影部分的面积是多少平方厘米?
20.求图中阴影部分的面积.(单位:厘米)
答 案
一、单选题
1. C 2. A 3. B 4. B 5. C
二、判断题
6. 正确 7. 正确 8. 正确 9. 错误
三、填空题
10. 5.375;12.5 11. (1)643(2)41.04
12. 6;3;18.84;28.26;72;15.48 13. =;=;= 14. 12;5
四、计算题
15. 解:8÷2=4(厘米),
4×4÷2×4,=16÷2×4,=8×4,=32(平方厘米);
答:阴影部分的面积是32平方厘米
16. 解:6×4÷2﹣3.14×62× , =24÷2﹣3.14×36× ,=12﹣9.42,=2.58(平方厘米);
答:阴影部分①比阴影部分②的面积多2.58平方厘米
五、解答题
17. 解:(3+6)×2-5+3.14×5÷2
=18-5+7.85=13+7.85=20.85(分米)
3×6-(5÷2)2×3.14÷2
=18-2.5×2.5×3.14÷2=18-9.8125=8.1875(平方分米)
18. 解:30×30+30×25=900+750 =1650(cm2)
六、应用题
19. 解:阴影部分面积为
答:阴影部分的面积是14平方厘米.
20. 解:[(5+8+5)×5÷2﹣ ×3.14×52]+( ×3.14×52﹣5×5÷2),
=[18×5÷2﹣0.785×25]+(0.785×25﹣25÷2),
=[90÷2﹣19.625]+(19.625﹣12.5),
=[45﹣19.625]+7.125,
=25.375+7.125,
=32.5(平方厘米);
答:阴影部分的面积为32.5平方厘米
(
第
1
页 共
6
页
)
同课章节目录
