第4单元可能性必考题检测卷(单元测试) 小学数学五年级上册人教版(含答案)
文档属性
| 名称 | 第4单元可能性必考题检测卷(单元测试) 小学数学五年级上册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-11-01 13:31:06 | ||
图片预览


文档简介
第4单元可能性必考题检测卷(单元测试)-小学数学五年级上册人教版
一、选择题
1.盒子里有大小、形状相同的白球、黑球共16个,如果任意摸一个球,摸到白球的可能性大,则白球至少要有( )个。
A.7 B.8 C.9 D.15
2.盒子里有红球2个、白球1个、黄球9个(这些球除颜色外完全相同)。从盒子里任意摸出一个球,下面说法正确的是( )。
A.一定摸出黄球 B.不可能摸出白球
C.摸出黄球的可能性最大 D.有可能摸出绿球
3.下表是去年某地新出生的男孩名字中使用率最高的前五个字,下面哪一句话表述正确?( )
名字 男孩人数
杰 549
宇 534
泽 453
博 443
浩 442
A.新出生的男孩叫“宇”比叫“博”的可能性要大。
B.新出生的男孩一定叫“杰”。
C.新出生的男孩叫“泽”比叫“浩”的可能性要小。
D.新出生的男孩不可能叫“哲”。
4.一种福利彩票的中奖率是,周宇买了10000张彩票,他( )中奖。
A.一定 B.不可能 C.可能
5.淘气做摸球游戏,她摸了30次,其中摸到红球7次,黄球23次,根据数据推测,她最有可能是在下面( )盒子里摸的。
A.10个黄球 B.8个红球,2个黄球
C.5个红球,5个黄球 D.8个黄球,2个红球
6.现在暗箱里有1个红球和7个黄球,如果摸一次( )。
A.一定能摸到黄球 B.摸到黄球的可能性大 C.一定不能摸到红球
7.一个盒子中装有9个大小和材质相同的球,其中有7个白球、2个红球。一次摸出1个,然后放回摇匀再摸。下面说法正确的是( )。
A.摸到白球的可能性最大
B.第一次不可能摸到红球
C.第一次摸到红球,第二次一定摸到白球
D.连续5次都摸到白球,第六次一定摸到红球
8.同学们玩摸球游戏,不透明的袋子中只有颜色不同,其它完全相同的红球和白球,前10次摸球的结果如下表。下面描述正确的是( )。
种类 红球 白球
次数 5 5
A.再摸一次可能会摸到白球 B.再摸一次一定能摸到红球
C.红球一定和白球同样多 D.红球不可能和白球同样多
9.下边盒子中的球除颜色外,其他均相同,从中任意摸出两个球,可能有( )种结果。
A.9 B.6 C.3 D.2
10.下面的游戏( )是不公平的。
A.抛硬币,正面朝上甲赢,反面朝上乙赢。
B.盒子里有2黄3红5个球,摸出黄球甲赢,摸出红球乙赢
C.石头、剪子、布定输赢
二、填空题
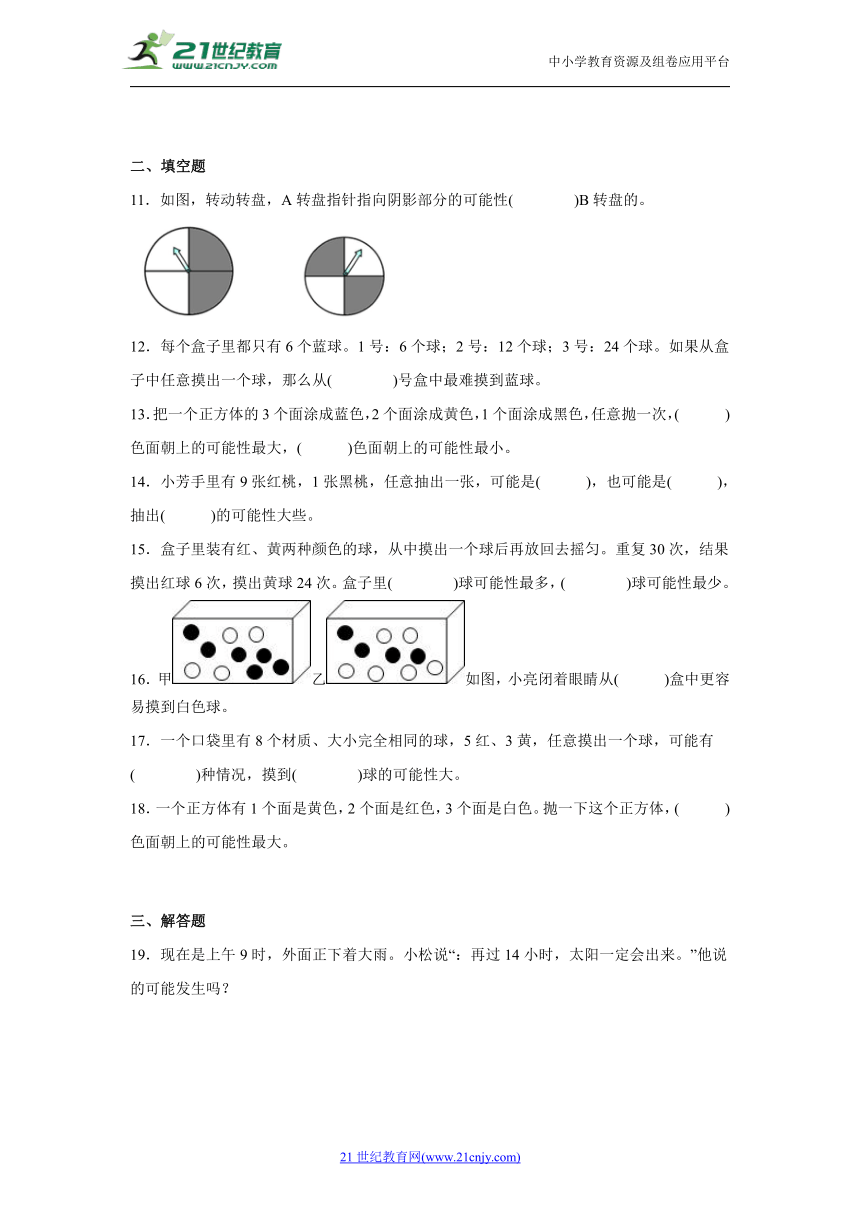
11.如图,转动转盘,A转盘指针指向阴影部分的可能性( )B转盘的。
12.每个盒子里都只有6个蓝球。1号:6个球;2号:12个球;3号:24个球。如果从盒子中任意摸出一个球,那么从( )号盒中最难摸到蓝球。
13.把一个正方体的3个面涂成蓝色,2个面涂成黄色,1个面涂成黑色,任意抛一次,( )色面朝上的可能性最大,( )色面朝上的可能性最小。
14.小芳手里有9张红桃,1张黑桃,任意抽出一张,可能是( ),也可能是( ),抽出( )的可能性大些。
15.盒子里装有红、黄两种颜色的球,从中摸出一个球后再放回去摇匀。重复30次,结果摸出红球6次,摸出黄球24次。盒子里( )球可能性最多,( )球可能性最少。
16.甲乙如图,小亮闭着眼睛从( )盒中更容易摸到白色球。
17.一个口袋里有8个材质、大小完全相同的球,5红、3黄,任意摸出一个球,可能有( )种情况,摸到( )球的可能性大。
18.一个正方体有1个面是黄色,2个面是红色,3个面是白色。抛一下这个正方体,( )色面朝上的可能性最大。
三、解答题
19.现在是上午9时,外面正下着大雨。小松说“:再过14小时,太阳一定会出来。”他说的可能发生吗?
20.盒子里有3个黑色球和3个白色球,除颜色外,球的大小、质地完全相同。小红和小云进行摸球游戏,从盒子里一次摸出两个球,摸出同色球算小红赢,摸出不同色的球算小云赢。谁赢的可能性大?
21.明明和小丽两人都有写着数字2,5,6,8的卡片各一张。每人拿出一张卡片,若两数的和是双数,则聪聪获胜;若两数的和是单数,则亮亮获胜。谁获胜的可能性大?你能换掉一张卡片使游戏更公平吗?
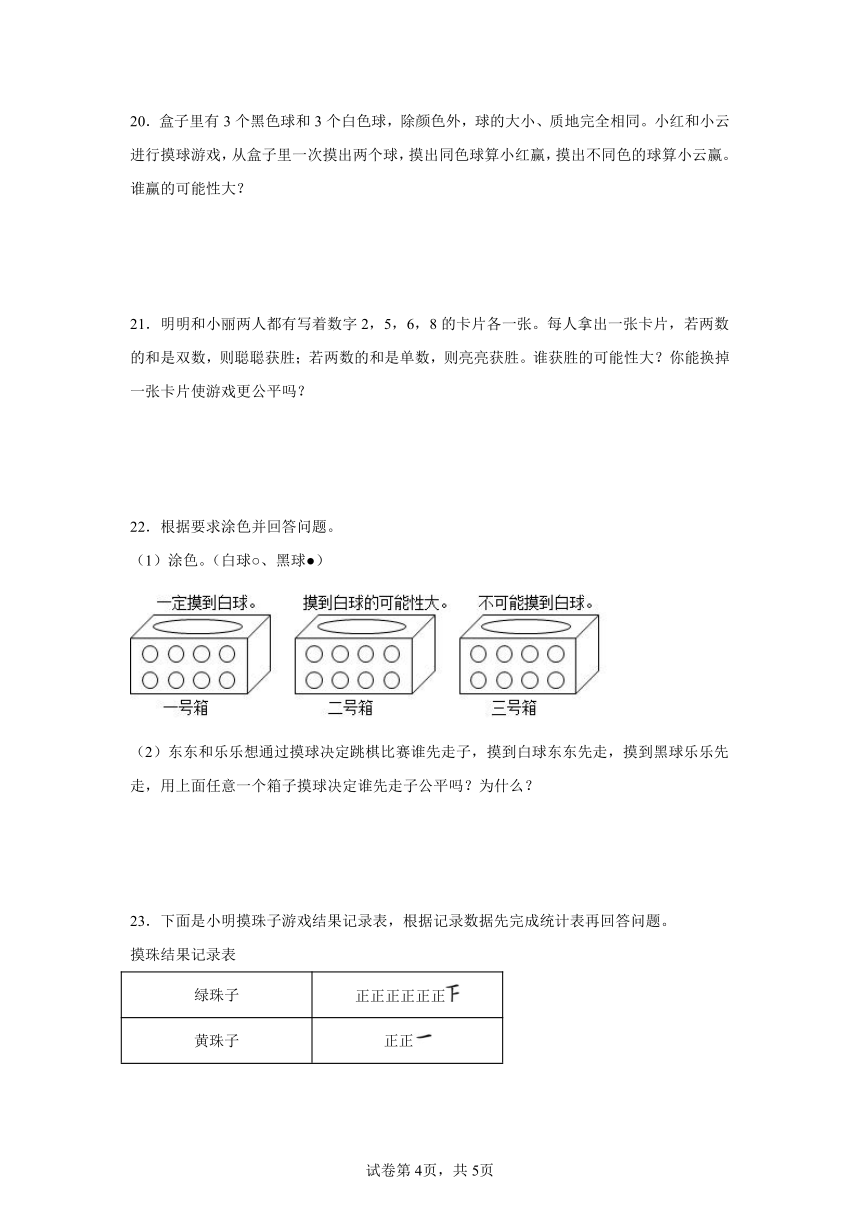
22.根据要求涂色并回答问题。
(1)涂色。(白球○、黑球●)
(2)东东和乐乐想通过摸球决定跳棋比赛谁先走子,摸到白球东东先走,摸到黑球乐乐先走,用上面任意一个箱子摸球决定谁先走子公平吗?为什么?
23.下面是小明摸珠子游戏结果记录表,根据记录数据先完成统计表再回答问题。
摸珠结果记录表
绿珠子 正正正正正正
黄珠子 正正
摸珠结果统计表
绿珠子 黄珠子 合计
次数
从表中可以看出:
(1)小明摸到绿珠子( )次,摸到黄珠子( )次,他一共摸了( )次。
(2)如果再摸8次,你认为摸到黄珠子的次数有可能比绿珠子多吗?请给正确答案下的涂色。
(3)要想使摸到两种球的次数接近相等,你会怎么办?
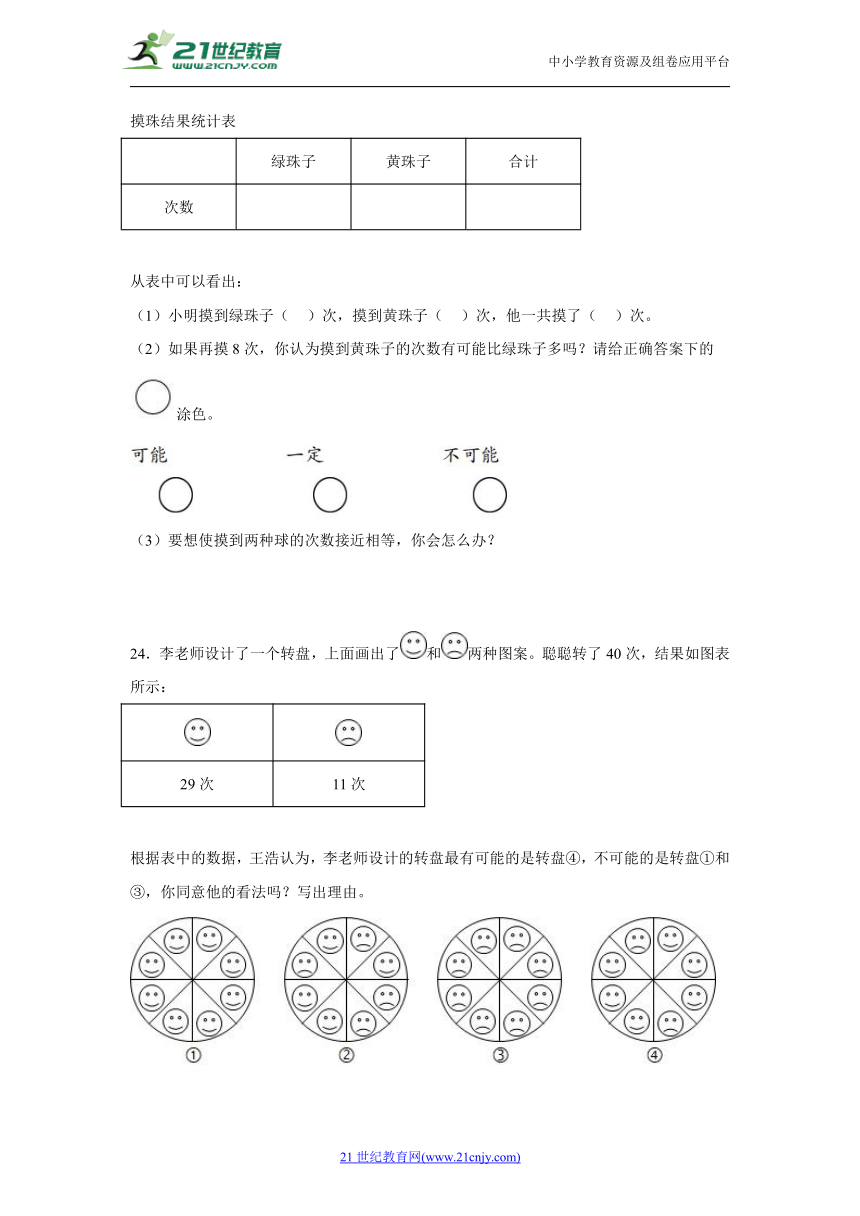
24.李老师设计了一个转盘,上面画出了和两种图案。聪聪转了40次,结果如图表所示:
29次 11次
根据表中的数据,王浩认为,李老师设计的转盘最有可能的是转盘④,不可能的是转盘①和③,你同意他的看法吗?写出理由。
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】可能性的大小与球数量的多少有关,数量多则被摸到的可能性较大,反之,则可能性就小,据此解答即可。
【详解】16÷2+1
=8+1
=9(个)
所以白球至少要有9个。
故答案为:C
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
2.C
【分析】由于盒子里有三种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,据此解答。
【详解】A.由于盒子里有三种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,所以一定摸出黄球是错误的;
B.由于盒子里面有白球,虽然摸出白球的可能性小,但不代表不可能摸出白球,所以这个说法也是错误的;
C.由于黄球的个数最多,所以摸出黄球的可能性最大,是正确的;
D.由于盒子里没有绿球,所以不可能摸出绿球,所以是错误的;
故答案为:C
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
3.A
【分析】哪个名字的人数越多,叫这个名字的可能性就越大;哪个名字的人数越少,叫这个名字的可能性就越小;表格中只是使用率最高的名字并不是全部,所以也有使用其它名字的可能性,据此解答。
【详解】A.由表格可知,新出生的男孩叫“宇”比叫“博”的可能性要大。
B.新出生的男孩可能叫“杰”,也可能不叫“杰”。
C.由表格可知,新出生的男孩叫“泽”比叫“浩”的可能性要大。
D.新出生的男孩有可能叫“哲”。
故答案为:A
【点睛】掌握事件发生可能性大小的判断方法是解答题目的关键。
4.C
【分析】判断事件发生的可能性的几种情况:可能、不可能、一定;结合生活实际,做出判断。
买福利彩票中奖属于不确定事件,无论买多少张彩票,中奖或不中奖都有可能,无法预料,据此解答。
【详解】一种福利彩票的中奖率是,周宇买了10000张彩票,他可能中奖。
故答案为:C
【点睛】关键是要明白中奖率只表示中奖可能性的大小,不能确定一定能中奖。
5.D
【分析】根据可能性的大小与数量的多少有关,数量多则摸到的可能性就大,反之被摸到的可能性就小。据此选择即可。
【详解】由分析可知:
摸到黄球的次数比摸到红球的次数多,所以盒子中黄球的个数比红球的个数多。
故答案为:D
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
6.B
【分析】箱子里哪种颜色球的数量越多,摸到该种颜色球的可能性就越大,箱子里哪种颜色球的数量越少,摸到该种颜色球的可能性就越小,据此解答。
【详解】箱子有红球和黄球两种颜色的球,任意摸一次,可能摸到黄球,也可能摸到红球,因为1<7,红球数量<黄球数量,所以摸到黄球的可能性大。
故答案为:B
【点睛】掌握判断事件发生可能性大小的方法是解答题目的关键。
7.A
【分析】从中摸出一个球后再放回去摇匀继续摸,则每次摸球的可能性不变。数量越多,摸到的可能性越大,因此直接比较数量即可知道可能性的大小关系。
【详解】A.因为白球最多,所以摸到白球的可能性最大,正确;
B.因为有2个红球,所以可能摸到红球,本选项说法错误;
C.因为从中摸出一个球后再放回去摇匀继续摸,则可能性不变。数量越多,摸到的可能性越大,所以第一次摸到红球,第二次可能摸到白球,本选项说法错误;
D.因为从中摸出一个球后再放回去摇匀继续摸,则可能性不变。数量越多,摸到的可能性越大,所以连续5次都摸到白球,第六次可能摸到红球,本选项说法错误。
故答案为:A
【点睛】此题考查可能性的大小比较方法,可以根据数量的多少来判断。
8.A
【分析】从统计表中可知,前10次摸球的结果红球和白球各是5次,虽然摸到红球和白球的次数相同,但不能说明再摸一次就一定会摸到哪种颜色的球,也不能说明红球和白球的数量哪个更多或同样多;据此解答。
【详解】A.再摸一次可能会摸到白球,原题说法正确;
B.再摸一次可能摸到红球,也可能摸到白球,原题说法错误;
C.红球不一定和白球同样多,原题说法错误;
D.红球可能和白球同样多,原题说法错误。
故答案为:A
【点睛】本题考查判断事件发生的可能性的几种情况:可能、不可能、一定;要结合实际,做出正确的判断。
9.B
【分析】这个盒子共有三种颜色的球,从中任意摸出两个球,可能是2个白球,可能是2个红球,可能是2个黄球,可能是1个白球1个红球,可能是1个白球1个黄球,可能是1个红球1个黄球。根据摸出球的结果解答即可。
【详解】根据分析得,从盒子中任意摸出两个球,可能有6种结果。
故答案为:B
【点睛】本题主要考查列举法解决问题,关键是利用列举法找到这组数据出现的规律,并利用规律做题。
10.B
【分析】当事件发生的可能性相等时,游戏是公平的;分别求出各个事件发生的可能性大小,然后进行判断。
【详解】A.因为硬币只有正反两面,正、反的可能性相等,所以公平;
B.盒子里有2黄3红5个球,因为黄球与红球的数量不相等,摸出红球可能性更大,所以游戏不公平;
C.石头、剪子、布定输赢,因为赢的可能性都是三分之一,所以公平。
故答案为:B
【点睛】事件发生的可能性与数量的多少有关,数量越多,发生的可能性就越大。
11.等于
【分析】A转盘中,整个圆被平均分成4份,其中阴影部分占2份,空白部分占2份,所以指针指向阴影部分和指向空白部分的可能性是一样大;B转盘中,整个圆也被平均分成4份,其中阴影部分占2份,空白部分占2份,所以指针指向阴影部分和指向空白部分的可能性是一样大;据此解答。
【详解】根据分析得,A转盘指针指向阴影部分的可能性是;
B转盘指针指向阴影部分的可能性是;
所以A转盘指针指向阴影部分的可能性等于B转盘指针指向阴影部分的可能性。
【点睛】此题主要考查可能性的大小,通过图形求出两个图形指向阴影部分的可能性都是,从而说明两个转盘指向阴影部分的可能性一样大。
12.3
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。据此解答。
【详解】1号盒子里面全是蓝球,从这个盒子一定能摸出蓝球;
2号盒子里有6个蓝球,还有6个是其它颜色的球,摸到蓝球的可能性小;
3号盒子里有6个蓝球,还有18个是其它颜色的球,摸到蓝球的可能性更小。
所以从3号盒中最难摸到蓝球。
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
13. 蓝色 黑色
【分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小。
【详解】3>2>1
把一个正方体的3个面涂成蓝色,2个面涂成黄色,1个面涂成黑色,任意抛一次,蓝色面朝上的可能性最大,黑色面朝上的可能性最小。
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
14. 红桃 黑桃 红桃
【分析】在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件;
根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小。
【详解】9>1
小芳手里有9张红桃,1张黑桃,任意抽出一张,可能是红桃,也可能是黑桃,抽出红桃的可能性大些。
【点睛】本题考查判断事件发生的可能性及可能性的大小,在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
15. 黄 红
【分析】可能事件发生的可能性有大小,相对数量多的可能性大一点,相对数量少的可能性小一点,据此解答。
【详解】盒子里装有红、黄两种颜色的球,摸出黄球的次数多于红球的次数,说明盒子里黄球数量比红球多,摸到黄球的可能性大,摸到红球可能性小。
【点睛】解答本题的关键是明确发生的可能性的大小与事物的数量有关。
16.乙
【分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大。
【详解】甲、乙盒内各有10个球,甲盒内的白色球有4个,乙盒内的白色球有6个;
6>4
所以小亮闭着眼睛从乙盒中更摸到白色球。
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
17. 2##两##二 红
【分析】任意摸出一个球,有几种颜色的球,摸出的结果就有几种可能的情况;哪种球的数量多,摸到哪种球的可能性就大,据此分析。
【详解】有红、黄两种颜色的球,任意摸出一个球,可能有2种情况;5>3,摸到红球的可能性大。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的球多,发生的可能性就大一些。
18.白
【分析】根据事件发生的可能性大小,哪种情况的数量多,事件发生的可能性就大;哪种情况的数量少,事件发生的可能性就小;据此判断。
【详解】3>2>1
抛一下这个正方体,白色面朝上的可能性最大。
【点睛】根据事件数量的多少可以判断事件发生的可能性大小。
19.一定不可能发生
【分析】事件的确定性:“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求写出即可。
【详解】9+14=23(时)
上午9时,再过14小时,正好是23时,是深夜,一定不会有太阳出来,因此小松说的一定不可能发生。
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
20.小云
【分析】由题意可知,3个黑色球和3个白色球,共6个球,每次摸出两个球,如图:
则共有15种组合,其中摸出同色球的情况:两黑,两白,共有6种组合;一黑一白的组合共有15-6=9种,据此解答即可。
【详解】每次摸出两个球共有15种情况,摸出同色球的情况共有6种。
15-6=9(种)
9>6
答:小云赢的可能性大。
【点睛】本题考查可能性,明确每次摸出两个球共有15种情况是解题的关键。
21.聪聪;见详解
【分析】先计算出两数的和的所有情况,再看和是双数、单数分别有几种情况,哪种情况出现越多,获胜的可能性就越大。
因为数字2,5,6,8中双数多,单数少,所以要用单数替换掉其中的一张双数的卡片,让游戏更公平。
【详解】两数的和:
2+2=4, 2+5=7,2+6=8,2+8=10;
5+2=7,5+5=10,5+6=11,5+8=13;
6+2=8,6+5=11,6+6=12,6+8=14;
8+2=10,8+5=13,8+6=14,8+8=16;
一共有16种情况,和为双数的有10种情况,和为单数的有6种情况;
10>6,所以聪聪获胜的可能大。
因为单数+单数=双数,双数+双数=双数,单数+双数=单数,所以把其中一张双数卡片换成单数卡数,和出现单数和双数的可能性相等,两人获胜的可能性相等。
答:聪聪获胜的可能大。把写着数字2的卡片都换成写着数字3的卡片,这样游戏更公平。(方法不唯一)
【点睛】本题考查可能性的大小以及游戏的公平性,要使游戏公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
22.(1)(2)见详解
【分析】(1)一号箱一定要摸到白球,那么不能有黑球,8个球都要为白球,一号箱不涂色即可;二号箱摸到白球的可能性大,只需要满足白球的数量比黑球的数量多,白球至少要5颗(含5颗)以上,又不能全是白球,黑球至少涂一颗;三号箱不可能摸到白球,全部涂成黑球,即可满足条件。据此完成涂色。
(2)摸到白球东东先走,摸到黑球乐乐先走,如果盒子里白球、黑球的个数相同,游戏规则公平,否则,游戏规则不公平。
【详解】(1)涂色如下:
(2)答:用上面任意一个箱子摸球决定谁先走子不公平,因为这三个箱子里,任一箱子都不满足白球、黑球的数量相同,所以游戏规则不公平。
【点睛】此题主要考查可能性的大小以及判断规则是否公平,关键是看参与游戏者出现的可能性是否相同。
23.见详解
(1)33;11;44
(2)见详解
(3)增加黄珠子的数量或者减少绿珠子的数量
【分析】根据记录表中的信息统计出摸到绿珠子和黄珠子的次数,再相加求出合计,完成统计表;
(1)根据统计表提供的信息进行解答;
(2)虽然摸到绿珠子的次数多,但由于事情的偶然性,则摸到黄珠子的次数也可能会多于绿珠子的次数,据此解答;
(3)增加黄珠子的数量或减少绿珠子的数量,使绿珠子的数量和黄珠子的数量相近,即摸到两种珠子的次数相近。
【详解】
绿珠子 黄珠子 合计
次数 33 11 44
(1)小明摸到绿珠子33次,摸到黄珠子11次,他一共摸了44次;
(2)
(3)增加黄珠子的数量或者减少绿珠子的数量。
【点睛】掌握可能性的大小与珠子数目的关系是解答本题的关键。
24.同意,理由见解析
【分析】聪聪一个转了40次,停在有29次,停在有11次,转盘上既有,又有,而且停在的次数大于停在,由此可知,转盘上的图案比多,据此逐项分析进行解答。
【详解】①转盘没有,①转盘不可能;
②转盘和相同,出现的可能性次数等于次数;
③转盘没有图形,③转盘不可能;
④转盘图像>图像,出现的可能性次数>次数。
由此可知,李老师设计的转盘最有可能是④,我同意王浩的看法。
【点睛】本题考查可能性的大小,某种情况所占的份数越多,出现该情况的可能性就越多,结合日常生活进行解答。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.盒子里有大小、形状相同的白球、黑球共16个,如果任意摸一个球,摸到白球的可能性大,则白球至少要有( )个。
A.7 B.8 C.9 D.15
2.盒子里有红球2个、白球1个、黄球9个(这些球除颜色外完全相同)。从盒子里任意摸出一个球,下面说法正确的是( )。
A.一定摸出黄球 B.不可能摸出白球
C.摸出黄球的可能性最大 D.有可能摸出绿球
3.下表是去年某地新出生的男孩名字中使用率最高的前五个字,下面哪一句话表述正确?( )
名字 男孩人数
杰 549
宇 534
泽 453
博 443
浩 442
A.新出生的男孩叫“宇”比叫“博”的可能性要大。
B.新出生的男孩一定叫“杰”。
C.新出生的男孩叫“泽”比叫“浩”的可能性要小。
D.新出生的男孩不可能叫“哲”。
4.一种福利彩票的中奖率是,周宇买了10000张彩票,他( )中奖。
A.一定 B.不可能 C.可能
5.淘气做摸球游戏,她摸了30次,其中摸到红球7次,黄球23次,根据数据推测,她最有可能是在下面( )盒子里摸的。
A.10个黄球 B.8个红球,2个黄球
C.5个红球,5个黄球 D.8个黄球,2个红球
6.现在暗箱里有1个红球和7个黄球,如果摸一次( )。
A.一定能摸到黄球 B.摸到黄球的可能性大 C.一定不能摸到红球
7.一个盒子中装有9个大小和材质相同的球,其中有7个白球、2个红球。一次摸出1个,然后放回摇匀再摸。下面说法正确的是( )。
A.摸到白球的可能性最大
B.第一次不可能摸到红球
C.第一次摸到红球,第二次一定摸到白球
D.连续5次都摸到白球,第六次一定摸到红球
8.同学们玩摸球游戏,不透明的袋子中只有颜色不同,其它完全相同的红球和白球,前10次摸球的结果如下表。下面描述正确的是( )。
种类 红球 白球
次数 5 5
A.再摸一次可能会摸到白球 B.再摸一次一定能摸到红球
C.红球一定和白球同样多 D.红球不可能和白球同样多
9.下边盒子中的球除颜色外,其他均相同,从中任意摸出两个球,可能有( )种结果。
A.9 B.6 C.3 D.2
10.下面的游戏( )是不公平的。
A.抛硬币,正面朝上甲赢,反面朝上乙赢。
B.盒子里有2黄3红5个球,摸出黄球甲赢,摸出红球乙赢
C.石头、剪子、布定输赢
二、填空题
11.如图,转动转盘,A转盘指针指向阴影部分的可能性( )B转盘的。
12.每个盒子里都只有6个蓝球。1号:6个球;2号:12个球;3号:24个球。如果从盒子中任意摸出一个球,那么从( )号盒中最难摸到蓝球。
13.把一个正方体的3个面涂成蓝色,2个面涂成黄色,1个面涂成黑色,任意抛一次,( )色面朝上的可能性最大,( )色面朝上的可能性最小。
14.小芳手里有9张红桃,1张黑桃,任意抽出一张,可能是( ),也可能是( ),抽出( )的可能性大些。
15.盒子里装有红、黄两种颜色的球,从中摸出一个球后再放回去摇匀。重复30次,结果摸出红球6次,摸出黄球24次。盒子里( )球可能性最多,( )球可能性最少。
16.甲乙如图,小亮闭着眼睛从( )盒中更容易摸到白色球。
17.一个口袋里有8个材质、大小完全相同的球,5红、3黄,任意摸出一个球,可能有( )种情况,摸到( )球的可能性大。
18.一个正方体有1个面是黄色,2个面是红色,3个面是白色。抛一下这个正方体,( )色面朝上的可能性最大。
三、解答题
19.现在是上午9时,外面正下着大雨。小松说“:再过14小时,太阳一定会出来。”他说的可能发生吗?
20.盒子里有3个黑色球和3个白色球,除颜色外,球的大小、质地完全相同。小红和小云进行摸球游戏,从盒子里一次摸出两个球,摸出同色球算小红赢,摸出不同色的球算小云赢。谁赢的可能性大?
21.明明和小丽两人都有写着数字2,5,6,8的卡片各一张。每人拿出一张卡片,若两数的和是双数,则聪聪获胜;若两数的和是单数,则亮亮获胜。谁获胜的可能性大?你能换掉一张卡片使游戏更公平吗?
22.根据要求涂色并回答问题。
(1)涂色。(白球○、黑球●)
(2)东东和乐乐想通过摸球决定跳棋比赛谁先走子,摸到白球东东先走,摸到黑球乐乐先走,用上面任意一个箱子摸球决定谁先走子公平吗?为什么?
23.下面是小明摸珠子游戏结果记录表,根据记录数据先完成统计表再回答问题。
摸珠结果记录表
绿珠子 正正正正正正
黄珠子 正正
摸珠结果统计表
绿珠子 黄珠子 合计
次数
从表中可以看出:
(1)小明摸到绿珠子( )次,摸到黄珠子( )次,他一共摸了( )次。
(2)如果再摸8次,你认为摸到黄珠子的次数有可能比绿珠子多吗?请给正确答案下的涂色。
(3)要想使摸到两种球的次数接近相等,你会怎么办?
24.李老师设计了一个转盘,上面画出了和两种图案。聪聪转了40次,结果如图表所示:
29次 11次
根据表中的数据,王浩认为,李老师设计的转盘最有可能的是转盘④,不可能的是转盘①和③,你同意他的看法吗?写出理由。
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案:
1.C
【分析】可能性的大小与球数量的多少有关,数量多则被摸到的可能性较大,反之,则可能性就小,据此解答即可。
【详解】16÷2+1
=8+1
=9(个)
所以白球至少要有9个。
故答案为:C
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
2.C
【分析】由于盒子里有三种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,再根据不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,据此解答。
【详解】A.由于盒子里有三种颜色的球,所以从盒子里任意摸出一个球是什么颜色的是不确定事件,所以一定摸出黄球是错误的;
B.由于盒子里面有白球,虽然摸出白球的可能性小,但不代表不可能摸出白球,所以这个说法也是错误的;
C.由于黄球的个数最多,所以摸出黄球的可能性最大,是正确的;
D.由于盒子里没有绿球,所以不可能摸出绿球,所以是错误的;
故答案为:C
【点睛】本题考查可能性大小的判断,理解不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
3.A
【分析】哪个名字的人数越多,叫这个名字的可能性就越大;哪个名字的人数越少,叫这个名字的可能性就越小;表格中只是使用率最高的名字并不是全部,所以也有使用其它名字的可能性,据此解答。
【详解】A.由表格可知,新出生的男孩叫“宇”比叫“博”的可能性要大。
B.新出生的男孩可能叫“杰”,也可能不叫“杰”。
C.由表格可知,新出生的男孩叫“泽”比叫“浩”的可能性要大。
D.新出生的男孩有可能叫“哲”。
故答案为:A
【点睛】掌握事件发生可能性大小的判断方法是解答题目的关键。
4.C
【分析】判断事件发生的可能性的几种情况:可能、不可能、一定;结合生活实际,做出判断。
买福利彩票中奖属于不确定事件,无论买多少张彩票,中奖或不中奖都有可能,无法预料,据此解答。
【详解】一种福利彩票的中奖率是,周宇买了10000张彩票,他可能中奖。
故答案为:C
【点睛】关键是要明白中奖率只表示中奖可能性的大小,不能确定一定能中奖。
5.D
【分析】根据可能性的大小与数量的多少有关,数量多则摸到的可能性就大,反之被摸到的可能性就小。据此选择即可。
【详解】由分析可知:
摸到黄球的次数比摸到红球的次数多,所以盒子中黄球的个数比红球的个数多。
故答案为:D
【点睛】本题考查可能性,明确可能性的大小与数量的多少有关是解题的关键。
6.B
【分析】箱子里哪种颜色球的数量越多,摸到该种颜色球的可能性就越大,箱子里哪种颜色球的数量越少,摸到该种颜色球的可能性就越小,据此解答。
【详解】箱子有红球和黄球两种颜色的球,任意摸一次,可能摸到黄球,也可能摸到红球,因为1<7,红球数量<黄球数量,所以摸到黄球的可能性大。
故答案为:B
【点睛】掌握判断事件发生可能性大小的方法是解答题目的关键。
7.A
【分析】从中摸出一个球后再放回去摇匀继续摸,则每次摸球的可能性不变。数量越多,摸到的可能性越大,因此直接比较数量即可知道可能性的大小关系。
【详解】A.因为白球最多,所以摸到白球的可能性最大,正确;
B.因为有2个红球,所以可能摸到红球,本选项说法错误;
C.因为从中摸出一个球后再放回去摇匀继续摸,则可能性不变。数量越多,摸到的可能性越大,所以第一次摸到红球,第二次可能摸到白球,本选项说法错误;
D.因为从中摸出一个球后再放回去摇匀继续摸,则可能性不变。数量越多,摸到的可能性越大,所以连续5次都摸到白球,第六次可能摸到红球,本选项说法错误。
故答案为:A
【点睛】此题考查可能性的大小比较方法,可以根据数量的多少来判断。
8.A
【分析】从统计表中可知,前10次摸球的结果红球和白球各是5次,虽然摸到红球和白球的次数相同,但不能说明再摸一次就一定会摸到哪种颜色的球,也不能说明红球和白球的数量哪个更多或同样多;据此解答。
【详解】A.再摸一次可能会摸到白球,原题说法正确;
B.再摸一次可能摸到红球,也可能摸到白球,原题说法错误;
C.红球不一定和白球同样多,原题说法错误;
D.红球可能和白球同样多,原题说法错误。
故答案为:A
【点睛】本题考查判断事件发生的可能性的几种情况:可能、不可能、一定;要结合实际,做出正确的判断。
9.B
【分析】这个盒子共有三种颜色的球,从中任意摸出两个球,可能是2个白球,可能是2个红球,可能是2个黄球,可能是1个白球1个红球,可能是1个白球1个黄球,可能是1个红球1个黄球。根据摸出球的结果解答即可。
【详解】根据分析得,从盒子中任意摸出两个球,可能有6种结果。
故答案为:B
【点睛】本题主要考查列举法解决问题,关键是利用列举法找到这组数据出现的规律,并利用规律做题。
10.B
【分析】当事件发生的可能性相等时,游戏是公平的;分别求出各个事件发生的可能性大小,然后进行判断。
【详解】A.因为硬币只有正反两面,正、反的可能性相等,所以公平;
B.盒子里有2黄3红5个球,因为黄球与红球的数量不相等,摸出红球可能性更大,所以游戏不公平;
C.石头、剪子、布定输赢,因为赢的可能性都是三分之一,所以公平。
故答案为:B
【点睛】事件发生的可能性与数量的多少有关,数量越多,发生的可能性就越大。
11.等于
【分析】A转盘中,整个圆被平均分成4份,其中阴影部分占2份,空白部分占2份,所以指针指向阴影部分和指向空白部分的可能性是一样大;B转盘中,整个圆也被平均分成4份,其中阴影部分占2份,空白部分占2份,所以指针指向阴影部分和指向空白部分的可能性是一样大;据此解答。
【详解】根据分析得,A转盘指针指向阴影部分的可能性是;
B转盘指针指向阴影部分的可能性是;
所以A转盘指针指向阴影部分的可能性等于B转盘指针指向阴影部分的可能性。
【点睛】此题主要考查可能性的大小,通过图形求出两个图形指向阴影部分的可能性都是,从而说明两个转盘指向阴影部分的可能性一样大。
12.3
【分析】事件发生的可能性大小是不确定的,当数量相对较多时,它发生的可能性就大;反之数量相对较少时,可能性就小。据此解答。
【详解】1号盒子里面全是蓝球,从这个盒子一定能摸出蓝球;
2号盒子里有6个蓝球,还有6个是其它颜色的球,摸到蓝球的可能性小;
3号盒子里有6个蓝球,还有18个是其它颜色的球,摸到蓝球的可能性更小。
所以从3号盒中最难摸到蓝球。
【点睛】本题考查可能性的大小,明确可能性的大小与数量的多少有关是解题的关键。
13. 蓝色 黑色
【分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小。
【详解】3>2>1
把一个正方体的3个面涂成蓝色,2个面涂成黄色,1个面涂成黑色,任意抛一次,蓝色面朝上的可能性最大,黑色面朝上的可能性最小。
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
14. 红桃 黑桃 红桃
【分析】在某种情况下会发生,而在其他情况下不会发生的事件,是“可能”事件;
根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小。
【详解】9>1
小芳手里有9张红桃,1张黑桃,任意抽出一张,可能是红桃,也可能是黑桃,抽出红桃的可能性大些。
【点睛】本题考查判断事件发生的可能性及可能性的大小,在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
15. 黄 红
【分析】可能事件发生的可能性有大小,相对数量多的可能性大一点,相对数量少的可能性小一点,据此解答。
【详解】盒子里装有红、黄两种颜色的球,摸出黄球的次数多于红球的次数,说明盒子里黄球数量比红球多,摸到黄球的可能性大,摸到红球可能性小。
【点睛】解答本题的关键是明确发生的可能性的大小与事物的数量有关。
16.乙
【分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大。
【详解】甲、乙盒内各有10个球,甲盒内的白色球有4个,乙盒内的白色球有6个;
6>4
所以小亮闭着眼睛从乙盒中更摸到白色球。
【点睛】在不需要计算出可能性大小的准确值时,根据事件数量的多少进行判断可能性的大小。
17. 2##两##二 红
【分析】任意摸出一个球,有几种颜色的球,摸出的结果就有几种可能的情况;哪种球的数量多,摸到哪种球的可能性就大,据此分析。
【详解】有红、黄两种颜色的球,任意摸出一个球,可能有2种情况;5>3,摸到红球的可能性大。
【点睛】可能性的大小与事件的基本条件和发展过程等许多因素有关。哪种颜色的球多,发生的可能性就大一些。
18.白
【分析】根据事件发生的可能性大小,哪种情况的数量多,事件发生的可能性就大;哪种情况的数量少,事件发生的可能性就小;据此判断。
【详解】3>2>1
抛一下这个正方体,白色面朝上的可能性最大。
【点睛】根据事件数量的多少可以判断事件发生的可能性大小。
19.一定不可能发生
【分析】事件的确定性:“一定”表示确定事件,“可能”表示不确定事件,“不可能”属于确定事件中的必然事件,结合实际生活,按要求写出即可。
【详解】9+14=23(时)
上午9时,再过14小时,正好是23时,是深夜,一定不会有太阳出来,因此小松说的一定不可能发生。
【点睛】此题考查的是事件的确定性和不确定性,应明确事件的确定性和不确定性,并能结合实际进行正确判断。
20.小云
【分析】由题意可知,3个黑色球和3个白色球,共6个球,每次摸出两个球,如图:
则共有15种组合,其中摸出同色球的情况:两黑,两白,共有6种组合;一黑一白的组合共有15-6=9种,据此解答即可。
【详解】每次摸出两个球共有15种情况,摸出同色球的情况共有6种。
15-6=9(种)
9>6
答:小云赢的可能性大。
【点睛】本题考查可能性,明确每次摸出两个球共有15种情况是解题的关键。
21.聪聪;见详解
【分析】先计算出两数的和的所有情况,再看和是双数、单数分别有几种情况,哪种情况出现越多,获胜的可能性就越大。
因为数字2,5,6,8中双数多,单数少,所以要用单数替换掉其中的一张双数的卡片,让游戏更公平。
【详解】两数的和:
2+2=4, 2+5=7,2+6=8,2+8=10;
5+2=7,5+5=10,5+6=11,5+8=13;
6+2=8,6+5=11,6+6=12,6+8=14;
8+2=10,8+5=13,8+6=14,8+8=16;
一共有16种情况,和为双数的有10种情况,和为单数的有6种情况;
10>6,所以聪聪获胜的可能大。
因为单数+单数=双数,双数+双数=双数,单数+双数=单数,所以把其中一张双数卡片换成单数卡数,和出现单数和双数的可能性相等,两人获胜的可能性相等。
答:聪聪获胜的可能大。把写着数字2的卡片都换成写着数字3的卡片,这样游戏更公平。(方法不唯一)
【点睛】本题考查可能性的大小以及游戏的公平性,要使游戏公平,要先找出事件发生的所有可能,然后看对于游戏双方,获胜的可能性是否相同。若相同,则游戏规则公平;若不相同,则游戏规则不公平。
22.(1)(2)见详解
【分析】(1)一号箱一定要摸到白球,那么不能有黑球,8个球都要为白球,一号箱不涂色即可;二号箱摸到白球的可能性大,只需要满足白球的数量比黑球的数量多,白球至少要5颗(含5颗)以上,又不能全是白球,黑球至少涂一颗;三号箱不可能摸到白球,全部涂成黑球,即可满足条件。据此完成涂色。
(2)摸到白球东东先走,摸到黑球乐乐先走,如果盒子里白球、黑球的个数相同,游戏规则公平,否则,游戏规则不公平。
【详解】(1)涂色如下:
(2)答:用上面任意一个箱子摸球决定谁先走子不公平,因为这三个箱子里,任一箱子都不满足白球、黑球的数量相同,所以游戏规则不公平。
【点睛】此题主要考查可能性的大小以及判断规则是否公平,关键是看参与游戏者出现的可能性是否相同。
23.见详解
(1)33;11;44
(2)见详解
(3)增加黄珠子的数量或者减少绿珠子的数量
【分析】根据记录表中的信息统计出摸到绿珠子和黄珠子的次数,再相加求出合计,完成统计表;
(1)根据统计表提供的信息进行解答;
(2)虽然摸到绿珠子的次数多,但由于事情的偶然性,则摸到黄珠子的次数也可能会多于绿珠子的次数,据此解答;
(3)增加黄珠子的数量或减少绿珠子的数量,使绿珠子的数量和黄珠子的数量相近,即摸到两种珠子的次数相近。
【详解】
绿珠子 黄珠子 合计
次数 33 11 44
(1)小明摸到绿珠子33次,摸到黄珠子11次,他一共摸了44次;
(2)
(3)增加黄珠子的数量或者减少绿珠子的数量。
【点睛】掌握可能性的大小与珠子数目的关系是解答本题的关键。
24.同意,理由见解析
【分析】聪聪一个转了40次,停在有29次,停在有11次,转盘上既有,又有,而且停在的次数大于停在,由此可知,转盘上的图案比多,据此逐项分析进行解答。
【详解】①转盘没有,①转盘不可能;
②转盘和相同,出现的可能性次数等于次数;
③转盘没有图形,③转盘不可能;
④转盘图像>图像,出现的可能性次数>次数。
由此可知,李老师设计的转盘最有可能是④,我同意王浩的看法。
【点睛】本题考查可能性的大小,某种情况所占的份数越多,出现该情况的可能性就越多,结合日常生活进行解答。
答案第1页,共2页
答案第1页,共2页
