《定积分的概念》教学设计
图片预览

文档简介
二、教材分析
《定积分的概念》是人教版高中选修系列2-1,第一章第五节的内容,在导数学习之后,定积分概念的建立为微积分基本定理的引出做了铺垫,起到了承上启下的作用。而且定积分概念的引人体现着微积分“无限分割、无穷累加”“以直代曲、以不变代变”的基本思想。所以,无论从内容还是数学思想方面,本次课在教材中都处于重要的地位。
三、学生分析
1.学生方面
具备了基本的数学能力和数学素养,但对于概念性的学习,特别是概念性的知识运用方面存在着一定困难。
2.数学思想方面
学生已具备一定的极限和微分思想的基础。
四、教法学法分析
1.在本节教学过程中,主要采用“问题教学法”,在教学过程中引导启发,培养学生“发现问题、提出问题、分析问题、解决问题”的能力以及交流与合作的能力,
2.学法方面(1)发现法解决第一个案例
(2)模仿法解决第二个案例
(3)归纳法总结出概念
(4)练习法巩固加深理解
五、教学过程
(一) 问题一:什么是曲边梯形?曲边梯形面积怎么求?
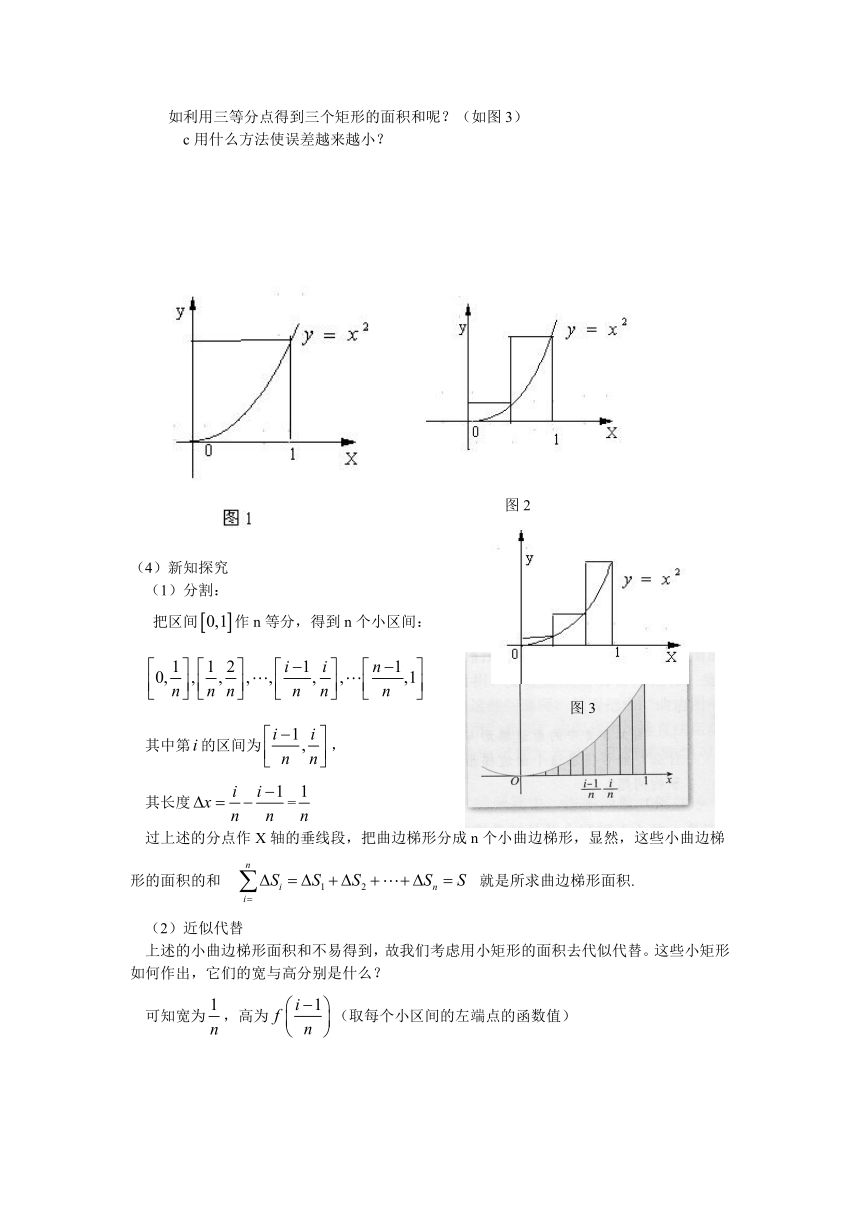
(1)先出示一个曲边梯形的图形,如图1
思考:如何求这个图形的面积?
(2)展示刘徽的“割圆术”
考虑用简单的图形来估计它的面积.用什么图形好呢?由于矩形面积=长×宽,最简单,
故用矩形的面积.
(3)设问:a用一个矩形的面积估计行吗?为什么?(误差太大了。)
b如果利用中点分割出两个矩形,(如图2)用它们的面积和来估计呢?误差会小一点吗?
如利用三等分点得到三个矩形的面积和呢?(如图3)
c用什么方法使误差越来越小?
(4)新知探究
(1)分割:
把区间作n等分,得到n个小区间:
其中第的区间为,
其长度=
过上述的分点作X轴的垂线段,把曲边梯形分成n个小曲边梯形,显然,这些小曲边梯形的面积的和 就是所求曲边梯形面积.
(2)近似代替
上述的小曲边梯形面积和不易得到,故我们考虑用小矩形的面积去代似代替。这些小矩形如何作出,它们的宽与高分别是什么?
可知宽为,高为(取每个小区间的左端点的函数值)
这样,在区间上,局部的
上“以曲代直”(即用小矩形面积代替
相应的小曲边梯形面积),则有
(3)求和
这些小矩形的面积和能否作为曲边梯形面积的近似值。我们来求这些小矩形的面积和。
记这些小矩形面积的和为,则
(注意公式: )
故
(4)取极限
当小矩形无限的增多,或近似值的极限就得到曲边梯形面积的精确值。
如何求出这个精确值呢?联想到用正多边形求圆的面积的方法,同样,用极限的方法求得。从而
。
∴ 在上,由函数与x轴围成的曲边梯形的面积是。
(二)问题二:汽车行驶的路程
汽车以速度组匀速直线运动时,经过时间所行驶的路程为.如果汽车作变速直线运动,在时刻的速度为(单位:km/h),那么它在0≤≤1(单位:h)这段时间内行驶的路程(单位:km)是多少?
分析:仿照问题一的求解,得出解题思路
1.分割
在时间区间上等间隔地插入个点,将区间等
分成个小区间:
,,…,
记第个区间为,其长度为
把汽车在时间段,,…,上行驶的路程分别记作:
,,…,
显然,
(2)近似代替
当很大,即很小时,在区间上,可以认为函数的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点处的函数值,从物理意义上看,即使汽车在时间段上的速度变化很小,不妨认为它近似地以时刻处的速度作匀速直线运动,即在局部小范围内“以匀速代变速”,于是的用小矩形的面积近似的代替,即在局部范围内“以直代取”,则有
①
(3)求和
由①,
==
==
从而得到的近似值
(4)取极限
当趋向于无穷大时,即趋向于0时,趋向于,从而有
(三)得出模型
从上面例子看出,不管是求曲边梯形的面积或是计算变速运动的路程,它们都归结为对问题的某些量进行“分割、近似代替、求和、取极限”,或者说都归结为形如 的和式极限问题。
(四)定积分的概念
一般地,设函数在区间上连续,用分点
将区间等分成个小区间,每个小区间长度为(),在每个小区间上取一点,作和式:
如果无限接近于(亦即)时,上述和式无限趋近于常数,那么称该常数为函数在区间上的定积分。记为:
其中成为被积函数,叫做积分变量,为积分区间,积分上限,积分下限。
说明:(1)定积分是一个常数,即无限趋近的常数(时)称为,而不是.
(2)用定义求定积分的一般方法是:①分割:等分区间;②近似代替:取点;③求和:;④取极限:
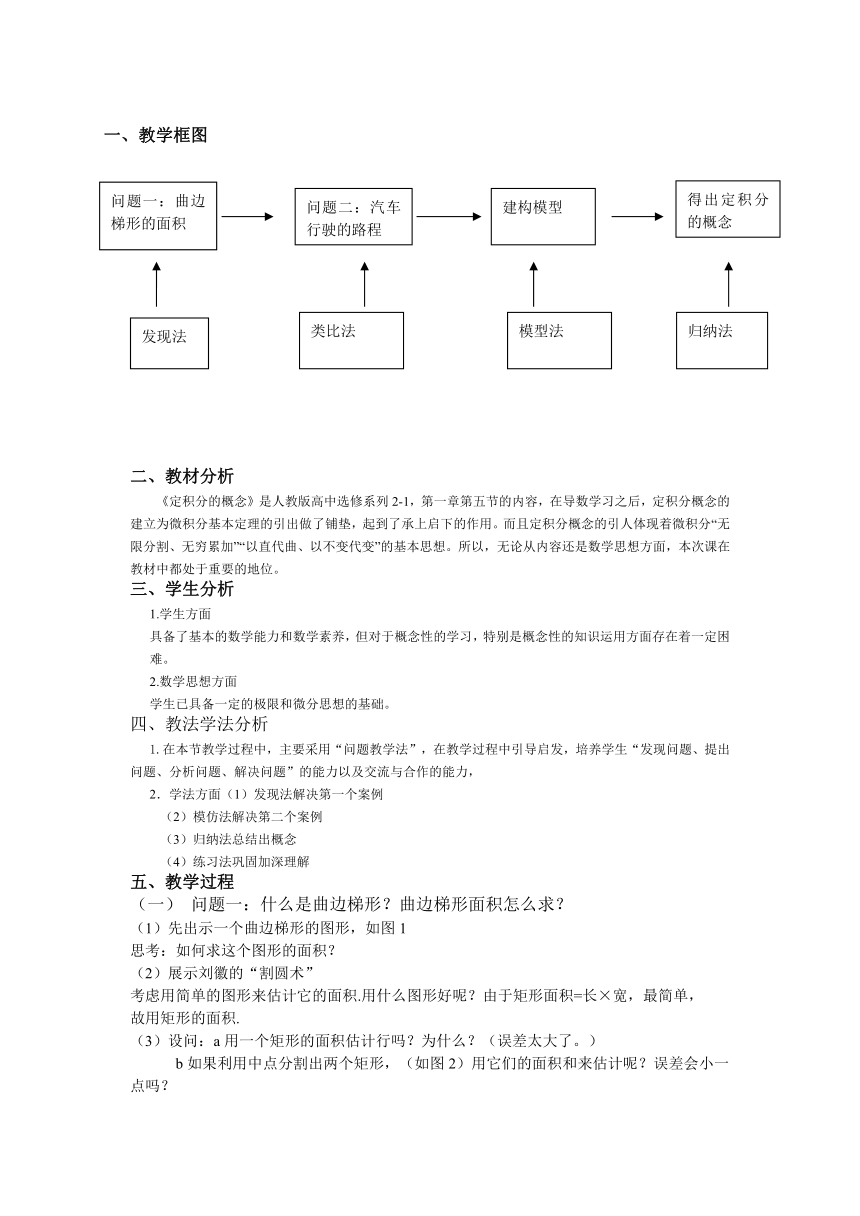
一、教学框图
问题一:曲边梯形的面积
问题二:汽车行驶的路程
建构模型
发现法
类比法
模型法
归纳法
得出定积分的概念
图2
图3
《定积分的概念》是人教版高中选修系列2-1,第一章第五节的内容,在导数学习之后,定积分概念的建立为微积分基本定理的引出做了铺垫,起到了承上启下的作用。而且定积分概念的引人体现着微积分“无限分割、无穷累加”“以直代曲、以不变代变”的基本思想。所以,无论从内容还是数学思想方面,本次课在教材中都处于重要的地位。
三、学生分析
1.学生方面
具备了基本的数学能力和数学素养,但对于概念性的学习,特别是概念性的知识运用方面存在着一定困难。
2.数学思想方面
学生已具备一定的极限和微分思想的基础。
四、教法学法分析
1.在本节教学过程中,主要采用“问题教学法”,在教学过程中引导启发,培养学生“发现问题、提出问题、分析问题、解决问题”的能力以及交流与合作的能力,
2.学法方面(1)发现法解决第一个案例
(2)模仿法解决第二个案例
(3)归纳法总结出概念
(4)练习法巩固加深理解
五、教学过程
(一) 问题一:什么是曲边梯形?曲边梯形面积怎么求?
(1)先出示一个曲边梯形的图形,如图1
思考:如何求这个图形的面积?
(2)展示刘徽的“割圆术”
考虑用简单的图形来估计它的面积.用什么图形好呢?由于矩形面积=长×宽,最简单,
故用矩形的面积.
(3)设问:a用一个矩形的面积估计行吗?为什么?(误差太大了。)
b如果利用中点分割出两个矩形,(如图2)用它们的面积和来估计呢?误差会小一点吗?
如利用三等分点得到三个矩形的面积和呢?(如图3)
c用什么方法使误差越来越小?
(4)新知探究
(1)分割:
把区间作n等分,得到n个小区间:
其中第的区间为,
其长度=
过上述的分点作X轴的垂线段,把曲边梯形分成n个小曲边梯形,显然,这些小曲边梯形的面积的和 就是所求曲边梯形面积.
(2)近似代替
上述的小曲边梯形面积和不易得到,故我们考虑用小矩形的面积去代似代替。这些小矩形如何作出,它们的宽与高分别是什么?
可知宽为,高为(取每个小区间的左端点的函数值)
这样,在区间上,局部的
上“以曲代直”(即用小矩形面积代替
相应的小曲边梯形面积),则有
(3)求和
这些小矩形的面积和能否作为曲边梯形面积的近似值。我们来求这些小矩形的面积和。
记这些小矩形面积的和为,则
(注意公式: )
故
(4)取极限
当小矩形无限的增多,或近似值的极限就得到曲边梯形面积的精确值。
如何求出这个精确值呢?联想到用正多边形求圆的面积的方法,同样,用极限的方法求得。从而
。
∴ 在上,由函数与x轴围成的曲边梯形的面积是。
(二)问题二:汽车行驶的路程
汽车以速度组匀速直线运动时,经过时间所行驶的路程为.如果汽车作变速直线运动,在时刻的速度为(单位:km/h),那么它在0≤≤1(单位:h)这段时间内行驶的路程(单位:km)是多少?
分析:仿照问题一的求解,得出解题思路
1.分割
在时间区间上等间隔地插入个点,将区间等
分成个小区间:
,,…,
记第个区间为,其长度为
把汽车在时间段,,…,上行驶的路程分别记作:
,,…,
显然,
(2)近似代替
当很大,即很小时,在区间上,可以认为函数的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点处的函数值,从物理意义上看,即使汽车在时间段上的速度变化很小,不妨认为它近似地以时刻处的速度作匀速直线运动,即在局部小范围内“以匀速代变速”,于是的用小矩形的面积近似的代替,即在局部范围内“以直代取”,则有
①
(3)求和
由①,
==
==
从而得到的近似值
(4)取极限
当趋向于无穷大时,即趋向于0时,趋向于,从而有
(三)得出模型
从上面例子看出,不管是求曲边梯形的面积或是计算变速运动的路程,它们都归结为对问题的某些量进行“分割、近似代替、求和、取极限”,或者说都归结为形如 的和式极限问题。
(四)定积分的概念
一般地,设函数在区间上连续,用分点
将区间等分成个小区间,每个小区间长度为(),在每个小区间上取一点,作和式:
如果无限接近于(亦即)时,上述和式无限趋近于常数,那么称该常数为函数在区间上的定积分。记为:
其中成为被积函数,叫做积分变量,为积分区间,积分上限,积分下限。
说明:(1)定积分是一个常数,即无限趋近的常数(时)称为,而不是.
(2)用定义求定积分的一般方法是:①分割:等分区间;②近似代替:取点;③求和:;④取极限:
一、教学框图
问题一:曲边梯形的面积
问题二:汽车行驶的路程
建构模型
发现法
类比法
模型法
归纳法
得出定积分的概念
图2
图3
